Flux d’un champ vectoriel
Qu’est-ce que le flux d’un champ vectoriel ?
Le flux d’un champ vectoriel \( V \) à travers une surface \( S \) de l’espace est une grandeur scalaire définie comme l’intégrale de surface du produit scalaire \( \vec{v}\cdot d\vec{s} \), évaluée point par point sur \( S \) : $$ \Phi_S = \int_S \vec{v} \cdot d\vec{s} $$
Ici, \( \vec{v} \) désigne les vecteurs du champ \( V \), tandis que \( d\vec{s} \) représente les vecteurs normaux infinitésimaux, orientés vers l’extérieur et perpendiculaires à chaque élément différentiel de surface de \( S \).
Le produit scalaire \( \vec{v} \cdot d\vec{s} \) en un point \( s \) de la surface constitue la contribution locale au flux.
$$ \vec{v} \cdot d\vec{s} $$
La somme de toutes ces contributions locales sur l’ensemble de la surface \( S \) définit le flux total du champ vectoriel à travers \( S \) :
$$ \Phi_S = \int_S \vec{v} \cdot d\vec{s} $$
Remarque : La surface \( S \) peut être ouverte ou fermée. Dans le cas d’une surface ouverte, l’orientation du vecteur normal est laissée au choix ; le flux est positif si le vecteur normal pointe vers l’extérieur, et négatif s’il pointe vers l’intérieur. Pour une surface fermée, les vecteurs normaux sont, par convention, orientés vers l’extérieur. Le flux à travers une surface fermée se note à l’aide d’une intégrale de surface circulée : $$ \Phi_S = \oint_S \vec{v} \cdot d\vec{s} $$
Exemple concret
Considérons une surface fermée et courbe \( S \).

On décompose la surface en éléments infinitésimaux \( s \).
Chaque petit élément peut alors être assimilé localement à un patch plan.
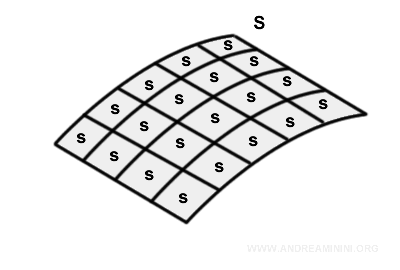
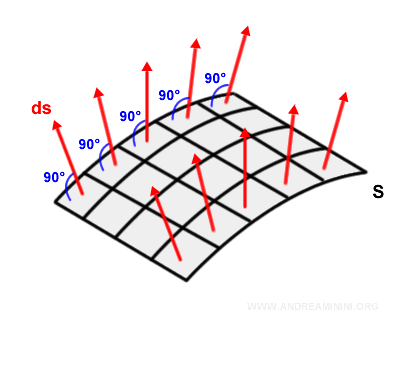
En chaque point \( s \), on associe le vecteur normal extérieur \( d\vec{s} \), dont la norme correspond à l’aire de l’élément différentiel considéré.
Un vecteur normal est par définition perpendiculaire au plan tangent local, c’est-à-dire qu’il forme un angle droit avec la surface en ce point.
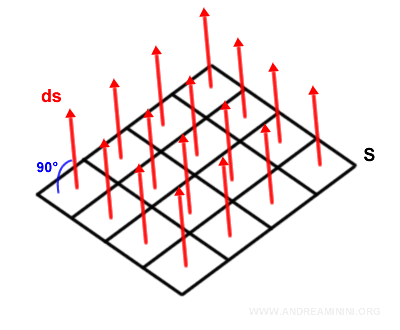
Remarque : Si la surface \( S \) était plane, tous les vecteurs normaux seraient parallèles entre eux. Le principe reste inchangé.
Introduisons maintenant un champ vectoriel \( V \) - par exemple un champ électrique ou magnétique.
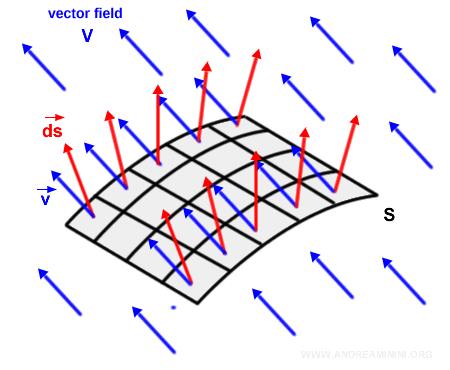
Remarque : Pour simplifier l’illustration, on représente ici un champ vectoriel constant, dont tous les vecteurs ont la même direction, la même norme et la même orientation. Le raisonnement s’étend sans difficulté aux champs plus généraux, où direction, norme et orientation varient.
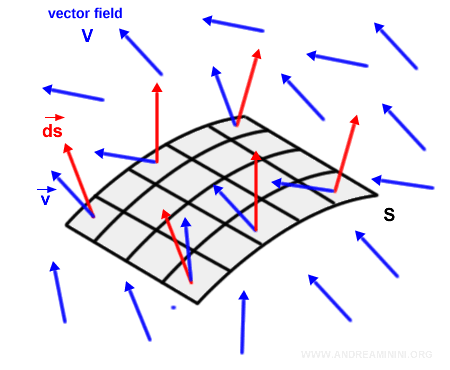
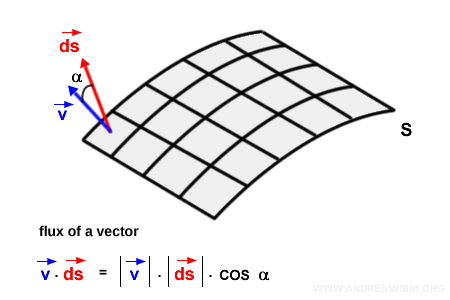
Pour chaque élément de surface \( s \), on calcule le produit scalaire entre le vecteur du champ \( \vec{v} \) et le vecteur normal \( d\vec{s} \).
Le produit scalaire de deux vecteurs est égal au produit de leurs normes \( |\vec{v}| \cdot |d\vec{s}| \), multiplié par le cosinus de l’angle \( \alpha \) qu’ils forment :
$$ \vec{v} \cdot d\vec{s} = |\vec{v}| \cdot |d\vec{s}| \cdot \cos \alpha $$
La contribution de chaque élément différentiel de surface \( s \) au flux correspond à ce produit scalaire local.
On répète ce calcul pour l’ensemble des éléments différentiels \( d\vec{s} \).
La valeur de \( \vec{v} \cdot d\vec{s} \) varie d’un point à l’autre, car l’angle entre le vecteur du champ et le vecteur normal change au long de la surface.
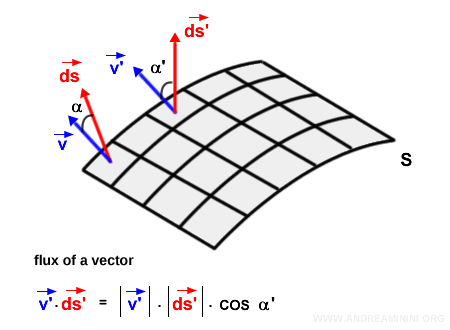
Remarque : Dans un champ vectoriel plus complexe, la direction et la norme des vecteurs peuvent également varier, ce qui modifie encore la valeur du produit scalaire local.
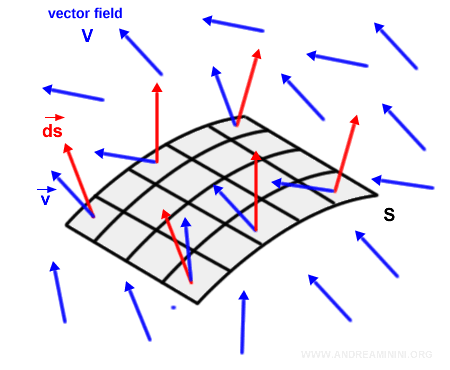
La somme de toutes les contributions locales sur la surface \( S \) fournit le flux total du champ vectoriel.
Comme il s’agit d’une somme étendue à une infinité d’éléments, elle s’exprime naturellement sous forme d’intégrale :
$$ \Phi_S = \int_S \vec{v} \cdot d\vec{s} $$
Remarque : Si \( S \) entoure un solide, le flux du champ vectoriel doit être calculé séparément pour chacune des faces de la surface qui le délimite. La démarche est identique dans chaque cas. Par exemple, pour un cube ou un parallélépipède rectangle, on évalue le flux sur chacune des six faces indépendamment.
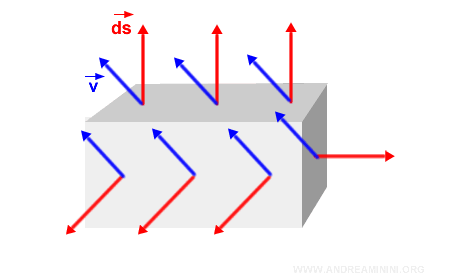
Et ainsi de suite.