Vecteurs axiaux (pseudovecteurs)

Un vecteur axial, aussi appelé pseudovecteur, est une grandeur vectorielle qui reste inchangée lorsqu'on effectue une réflexion spatiale, autrement dit une transformation de parité.

Les vecteurs axiaux se comportent comme les vecteurs ordinaires lorsqu'on fait tourner un système de référence. En revanche, leur comportement diffère lorsque l'on inverse les coordonnées spatiales à l'aide d'une transformation de parité (voir l'opérateur de parité).

Autrement dit, lors d'une transformation de parité, un vecteur ordinaire, ou vecteur polaire, change de sens, tandis qu'un vecteur axial conserve son orientation.

Pour comprendre concrètement cette différence, examinons un exemple simple.

Un exemple concret

Exemple d'un vecteur ordinaire

Considérons un vecteur ordinaire $ \vec v $.

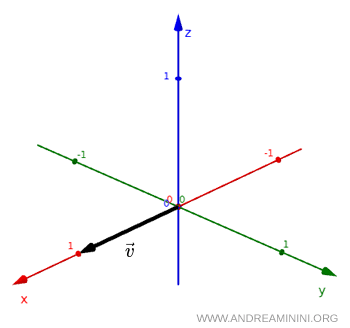
Si l'on effectue une inversion spatiale, c'est-à-dire $ x \to -x $ et $ y \to -y $, le vecteur devient son vecteur opposé $ - \vec v $.

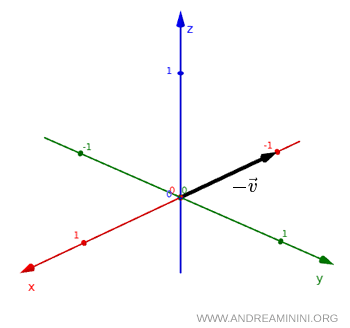
Le nouveau vecteur $ - \vec v $ conserve la même norme et la même direction géométrique, mais son sens est inversé par rapport au vecteur initial $ \vec v $.

Autrement dit, le vecteur change de signe lorsqu'on applique une inversion spatiale.

On peut donc dire que, dans un référentiel réfléchi, un vecteur ordinaire garde sa norme mais voit son orientation s'inverser.

Remarque. Parmi les exemples classiques de vecteurs ordinaires en physique figurent le déplacement, la vitesse et la force.

Un vecteur axial, en revanche, se comporte différemment : il reste invariant sous une réflexion spatiale.

Exemple d'un vecteur axial

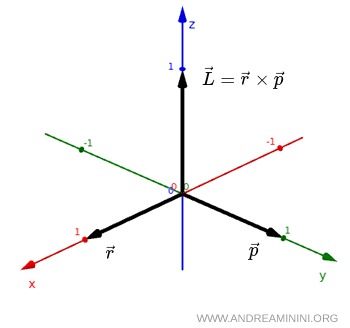
Un exemple emblématique de vecteur axial est le moment cinétique.

Si l'on considère un vecteur position $ \vec r $ et un vecteur quantité de mouvement $ \vec p $, le moment cinétique est défini par leur produit vectoriel :

$$ \vec L = \vec r \times \vec p $$

De manière générale, le produit vectoriel de deux vecteurs polaires donne toujours un vecteur axial.

Lors d'une réflexion spatiale, les vecteurs $ \vec r $ et $ \vec p $ deviennent respectivement $ - \vec r $ et $ - \vec p $. Toutefois, leur produit vectoriel conserve la même orientation.

$$ \vec L = \vec r \times \vec p = ( - \vec r ) \times ( - \vec p ) $$

Dans les deux cas, le vecteur $ \vec L $ reste perpendiculaire au plan défini par $ \vec r $ et $ \vec p $, et il pointe dans la même direction le long de l'axe $ z $.

 

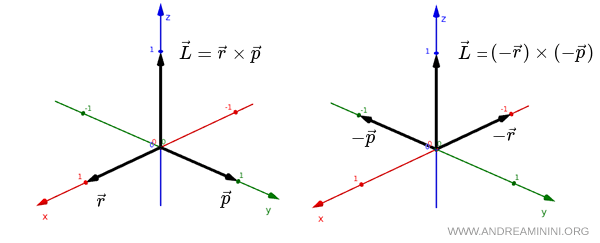
Autrement dit, le vecteur axial $ \vec L $ ne change pas de signe lorsqu'on effectue une inversion spatiale.

Remarque. D'autres exemples de vecteurs axiaux en physique sont la vitesse angulaire, le moment de force et le champ magnétique. Toutes ces grandeurs résultent d'un produit vectoriel.

Quelle est la signification physique des vecteurs axiaux ?

Les vecteurs axiaux mettent en évidence une propriété fondamentale de l'espace : certaines grandeurs physiques ne dépendent pas uniquement de la direction, mais aussi de l'orientation même de l'espace.

Pour cette raison, ils jouent un rôle central dans les phénomènes liés à la parité, en particulier dans le cadre des interactions fondamentales.

Ils sont notamment essentiels pour comprendre la violation de la parité dans l'interaction faible.

Et ainsi de suite.