Moment d’une force 

Le moment d’une force désigne l’aptitude d’une force à provoquer la rotation d’un objet autour d’un point ou d’un axe. La relation fondamentale est : $$ M = F \cdot d $$ où $F$ représente l’intensité de la force et $d$ le bras de levier (ou rayon), c’est-à-dire la distance perpendiculaire entre la ligne d’action de la force et le point de rotation (ou l’axe).

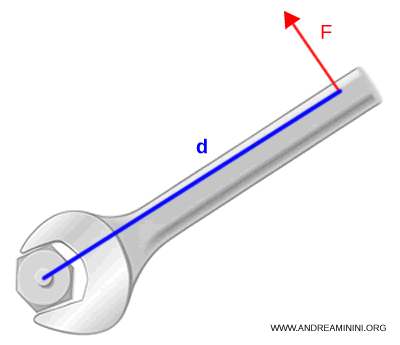
Si la force n’est pas appliquée perpendiculairement, le moment s’exprime par : $$ M = F \cdot d \cdot \sin \theta $$ où $\theta$ est l’angle formé entre la direction de la force et le bras de levier.

Ainsi, pour caractériser le moment d’une force, il ne suffit pas d’en connaître l’intensité : il faut aussi préciser son point d’application et son orientation par rapport à l’axe de rotation.

Par convention, on considère que le moment est :

• positif $(M > 0)$ lorsque la rotation se fait dans le sens trigonométrique (antihoraire),
• négatif $(M < 0)$ lorsque la rotation se fait dans le sens horaire.

Cette convention de signe peut néanmoins varier selon le domaine étudié.

Remarque. Lorsque plusieurs moments agissent simultanément, on attribue à chacun le signe correspondant à l’effet qu’il produirait s’il agissait seul. Le moment résultant est alors la somme algébrique de tous les moments élémentaires.

Exemple

Supposons que j’utilise une clé de 0,3 m pour desserrer une vis, en appliquant une force de 20 N perpendiculairement au bras de levier.

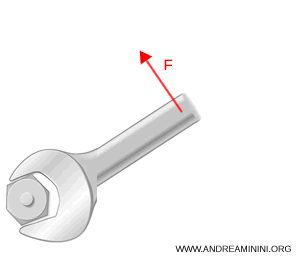
Le moment exercé sur la vis est alors de 6 N·m (newton-mètre) :

$$ M = 20 \times 0.3 = 6 \, \text{N·m} $$

Avec une clé deux fois plus longue (0,6 m), appliquant la même force de 20 N perpendiculairement,

$$ M = 20 \times 0.6 = 12 \, \text{N·m} $$

le moment est doublé.

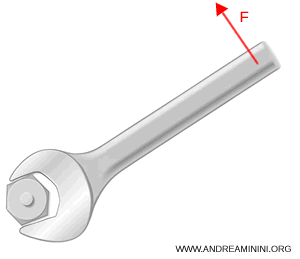
Cet exemple illustre clairement que plus le point d’application de la force est éloigné de l’axe, plus il est aisé de faire tourner la vis.

En d’autres termes : une clé plus longue permet d’obtenir le même effet avec moins d’effort, puisqu’elle accroît le moment sans qu’il soit nécessaire d’augmenter la force appliquée.

Remarque. Le même principe explique pourquoi les poignées de porte sont placées loin des gonds : pousser près des charnières exige bien davantage de force que d’actionner la poignée.

Par exemple, une force de 10 N appliquée à 1 mètre des gonds génère un moment de 10 N·m : $$ M = F \times d = 10 \ N \times 1 \ m = 10 \, \text{N·m} $$ En revanche, appliquée à seulement 0,2 m des gonds, il faudrait une force cinq fois plus grande pour obtenir le même moment ($ M = 10 \ N \cdot m $) : $$ F = \frac{M}{d} = \frac{10 \ N \cdot m}{0.2 \ m} = 50 \, \text{N} $$

La formule du moment d’une force

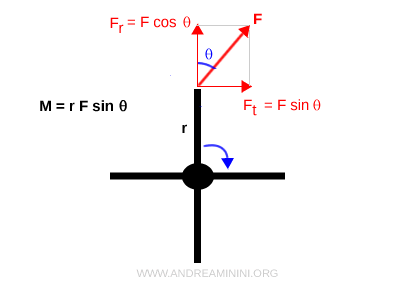
Lorsqu’une force $\vec{F}$ est appliquée en un point situé à une distance $ r $ de l’axe de rotation d’un corps rigide, elle peut engendrer un mouvement de rotation. Cet effet est mesuré par le moment $M$, défini par : $$ M = r F \sin \theta $$ où $\theta$ est l’angle entre le vecteur position et la direction de la force.

Si la force est appliquée radialement - c’est-à-dire le long du rayon reliant le point d’application à l’axe de rotation - le moment est nul : $ M = 0 $.

Dans ce cas, aucun mouvement de rotation n’apparaît.

En revanche, une force appliquée perpendiculairement au rayon produit un moment maximal, car l’intégralité de son intensité contribue alors à la rotation.

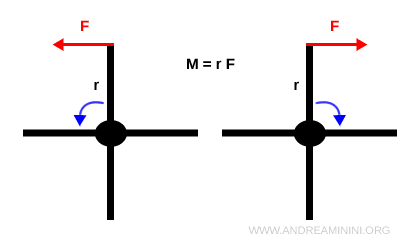
De manière générale, seule la composante tangentielle d’une force est efficace pour produire une rotation ; la composante radiale reste sans effet.

C’est pourquoi le moment d’une force se calcule en projetant cette force sur la direction tangentielle :

$$ M = r \, (F \sin \theta) $$

La composante radiale n’intervient donc pas.

Exercices

Exercice 1

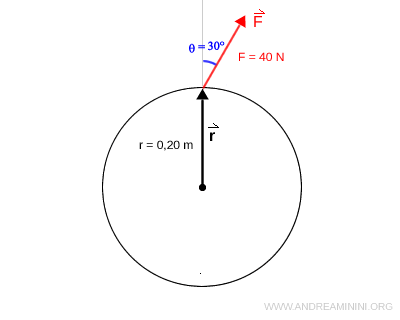
Déterminez le moment produit par une force $ F=40 \ N $ appliquée à une distance $ r = 0.20 \ m $ de l’axe de rotation, avec un angle de 30° par rapport au bras de levier.

La formule du moment est :

$$ M = r \cdot F \cdot \sin \theta $$

Ici, $ r $ représente la distance à l’axe de rotation, c’est-à-dire la longueur du bras de levier $ \vec{r} $. Dans ce cas, $ r = 0.20 \ m $.

$$ M = 0.20 \ m \cdot F \cdot \sin \theta $$

La force appliquée est $ F = 40 \ N $

$$ M = 0.20 \ m \cdot 40 \ N \cdot \sin \theta $$

L’angle entre le vecteur force $ \vec{F} $ et le bras de levier $ \vec{r} $ est $ \theta = 30° $.

$$ M = 0.20 \ m \cdot 40 \ N \cdot \sin 30° $$

Comme $ \sin 30° = \tfrac{1}{2} $,

$$ M = 0.20 \ m \cdot 40 \ N \cdot \tfrac{1}{2} $$

On obtient ainsi la composante tangentielle de la force : $ F_x = 40 \ N \cdot \tfrac{1}{2} = 20 \ N $

$$ M = 0.20 \ m \cdot 20 \ N $$

Le moment est donc égal à 4 newton-mètres.

$$ M = 4 \ Nm $$

Et ainsi de suite.