Les leviers en physique
Un levier est un solide rigide capable de tourner autour d’un point fixe, appelé point d’appui. Il fait partie des machines simples les plus fondamentales et reste, aujourd’hui encore, d’une efficacité remarquable. Le fonctionnement de tout levier repose toujours sur trois éléments essentiels:
- le point d’appui, autour duquel le levier pivote;
- la force appliquée \( F_M \), c’est-à-dire l’action exercée pour provoquer le mouvement;
- la force résistante \( F_R \), qui correspond à la force à vaincre, le plus souvent liée au poids d’un objet.
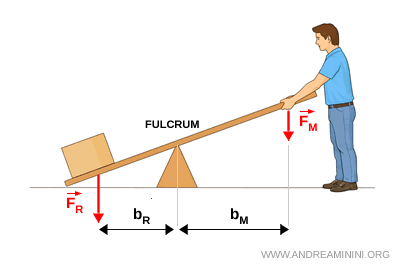
À chaque force est associé un bras de levier, défini comme la distance perpendiculaire entre le point d’appui et la ligne d’action de la force. On distingue ainsi:
- \( b_M \), le bras de la force appliquée;
- \( b_R \), le bras de la force résistante.
Les forces \( F_M \) et \( F_R \) sont équilibrées par la réaction exercée au point d’appui.
Pour que le levier soit en équilibre statique, la somme algébrique des moments des forces doit être nulle lorsque le point d’appui est choisi comme axe de rotation.
$$ b_R F_R = b_M F_M $$
Cette relation met en évidence un principe clé: on peut réduire l’intensité d’une force en augmentant son bras de levier, et inversement augmenter l’effort requis lorsque ce bras est raccourci.
Concrètement, pour soulever un objet lourd, il est avantageux d’appliquer la force \( F_M \) le plus loin possible du point d’appui. Le bras \( b_M \) augmente et l’effort nécessaire diminue.
D’un point de vue pratique, les leviers permettent d’équilibrer ou d’amplifier des forces afin de soulever, déplacer ou vaincre une résistance avec une efficacité accrue.
Un exemple concret
Considérons un levier en équilibre, pour lequel la relation suivante est vérifiée:
$$ b_R F_R = b_M F_M $$
Supposons que la force résistante soit:
$$ F_R = 100\ \text{N} $$
et que son bras de levier soit:
$$ b_R = 0.20\ \text{m} $$
Si la force appliquée agit à une distance d’un mètre du point d’appui, autrement dit si $ b_M = 1.00\ \text{m} $, la force appliquée nécessaire vaut:
$$ F_M = \frac{b_R}{b_M} F_R = \frac{0.20}{1.00} \cdot 100 = 20\ \text{N} $$
La force à exercer est donc nettement inférieure à la force résistante.
Remarque. Si la force appliquée était exercée à seulement dix centimètres du point d’appui, soit $ b_M = 0.10\ \text{m} $, la force nécessaire deviendrait beaucoup plus importante $$ F_M = \frac{0.20}{0.10} \cdot 100 = 200\ \text{N} $$ Dans ce cas, la force appliquée doit dépasser la force résistante.
On en déduit une règle simple: à force résistante identique, plus le bras de la force appliquée est grand, plus la force requise est faible, et inversement.
Leviers avantageux, désavantageux et neutres
Selon le rapport entre les longueurs des bras de levier, on distingue trois catégories de leviers.
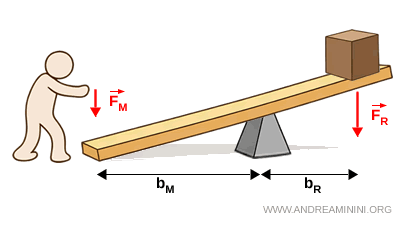
- Levier avantageux
Le levier est avantageux lorsque le bras de la force appliquée est plus long que celui de la force résistante $$
b_M > b_R $$ L’équilibre est alors obtenu avec une force appliquée plus faible $$ F_M < F_R $$ Ce type de levier permet de vaincre une résistance importante avec un effort réduit.
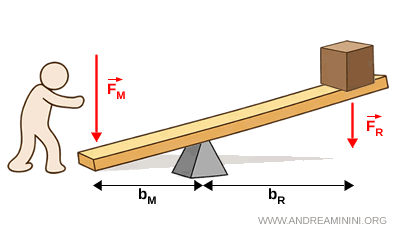
- Levier désavantageux
Le levier est dit désavantageux lorsque le bras de la force appliquée est plus court que celui de la force résistante $$ b_M < b_R
$$ L’équilibre exige alors une force appliquée plus grande $$ F_M > F_R
$$ Ce type de levier ne réduit pas l’effort, mais il est utile lorsqu’on recherche précision et rapidité de mouvement.
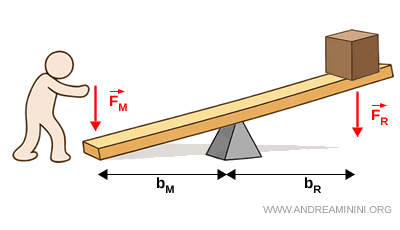
- Levier neutre
Le levier est neutre lorsque les deux bras ont la même longueur $$ b_M = b_R $$ La force appliquée est alors égale à la force résistante $$ F_M = F_R $$ Il n’y a ni gain ni perte mécanique en termes de force.
Types de leviers
Les leviers sont également classés en trois types selon la position relative du point d’appui, de la force appliquée et de la force résistante.
- Levier du premier genre
Le point d’appui se situe entre la force appliquée et la force résistante. Ce type de levier peut être avantageux, désavantageux ou neutre. Des exemples courants sont les ciseaux et les balançoires de jeux pour enfants.
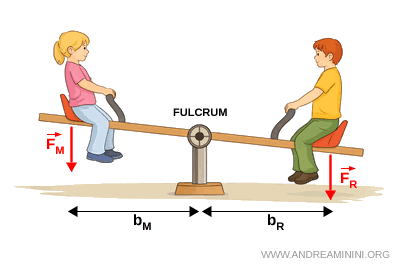
- Levier du deuxième genre
La force résistante est située entre le point d’appui et la force appliquée. Ce type de levier est toujours avantageux. On le rencontre notamment dans les brouettes, les casse-noix et les ouvre-bouteilles.
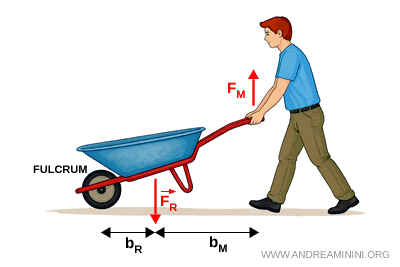
- Levier du troisième genre
- La force appliquée est située entre le point d’appui et la force résistante. Ce type de levier est toujours désavantageux, car le bras $ b_R $ est plus long que le bras $ b_M $. Il permet cependant d’effectuer des mouvements rapides et précis. Un exemple typique est celui des pinces.
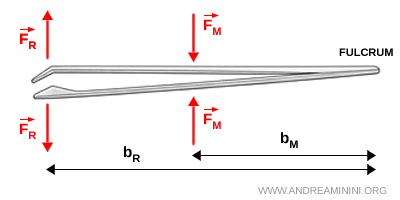
Ces trois catégories de leviers montrent que la position des forces joue souvent un rôle plus déterminant que leur intensité.
Grâce à une utilisation appropriée des bras de levier, une force modeste peut ainsi en vaincre une autre beaucoup plus importante.
Un exemple pratique
Un travailleur utilise un levier rigide pour soulever une caisse de masse 75 kg.
La caisse est placée à 0.40 m du point d'appui, tandis que la force motrice est exercée à l'extrémité opposée du levier, à une distance de 1.60 m du point d'appui.
Les données du problème sont:
- \( b_R = 0.40 \ \text{m} \)
- \( b_M = 1.60 \ \text{m} \)
- \( m = 75 \ \text{kg} \)
Quelle est la force résistante exercée par la caisse?
La force résistante correspond au poids de la caisse:
$$ F_R = P = mg $$
La masse vaut $ m = 75 \ \text{kg} $ et l'accélération de la pesanteur est \( g = 9.8 \ \text{N/kg} \).
$$ F_R = 75 \ (\text{kg}) \cdot 9.8 \ (\text{N/kg}) = 735 \ \text{N} $$
La force résistante appliquée au levier est donc:
$$ F_R = 735 \ \text{N} $$
Quelle force motrice faut-il appliquer pour maintenir l'équilibre du levier?
La condition d'équilibre statique d'un levier s'écrit:
$$ b_R F_R = b_M F_M $$
En isolant la force motrice \( F_M \), on obtient:
$$ F_M = \frac{b_R}{b_M} F_R = \frac{0.40}{1.60} \cdot 735 $$
$$ F_M = 0.25 \cdot 735 = 183.75 \ \text{N} \approx 184 \ \text{N} $$
La force motrice nécessaire pour assurer l'équilibre est donc:
$$ F_M \approx 184 \ \text{N} $$
Quel est le type de levier utilisé?
Un levier est mécaniquement avantageux lorsque \( b_M > b_R \).
Ici, $ b_M = 1.60 \ \text{m} $ et $ b_R = 0.40 \ \text{m} $. Le levier est donc mécaniquement avantageux.
L'avantage mécanique vaut:
$$ \frac{F_R}{F_M} = \frac{b_M}{b_R} = \frac{1.60}{0.40} = 4 $$
La force motrice est ainsi environ quatre fois plus faible que la force résistante.
Exercice 2
Un sac de masse $ m = 200 \ \text{kg} $ est placé à l'une des extrémités d'un levier du premier genre. À l'extrémité opposée, un travailleur applique une force motrice de $ F_M = 200 \ \text{N} $.
À quelle distance du sac doit être positionné le point d'appui pour que le levier soit en équilibre statique?
La condition d'équilibre d'un levier est:
$$ b_R F_R = b_M F_M $$
La force motrice est connue:
$$ F_M = 200 \ \text{N} $$
La force résistante est le poids du sac:
$$ F_R = mg = 200 \ (\text{kg}) \cdot 9.81 \ (\text{N/kg}) = 1962 \ \text{N} $$
En remplaçant dans l'équation d'équilibre:
$$ b_R \cdot 1962 = b_M \cdot 200 $$
On isole le bras résistant:
$$ b_R = \frac{b_M \cdot 200}{1962} $$
$$ b_R = b_M \cdot 0.102 $$
La longueur totale du levier étant $ L = b_R + b_M = 3.00 \ \text{m} $, on a:
$$ b_M = 3.00 \ \text{m} - b_R $$
En substituant:
$$ b_R = (3.00 \ \text{m} - b_R) \cdot 0.102 $$
$$ b_R = 0.306 \ \text{m} - 0.102 \, b_R $$
$$ b_R + 0.102 \, b_R = 0.306 \ \text{m} $$
$$ b_R \cdot 1.102 = 0.306 \ \text{m} $$
$$ b_R = \frac{0.306 \ \text{m}}{1.102} $$
$$ b_R \approx 0.28 \ \text{m} $$
En équilibre, le point d'appui doit donc se situer à environ $ 0.28 \ \text{m} $ du sac.
La longueur du bras moteur est alors:
$$ b_M = 3.00 - 0.28 = 2.72 \ \text{m} $$
Le levier est mécaniquement avantageux, puisque le bras moteur est nettement plus long que le bras résistant.
Exercice 3
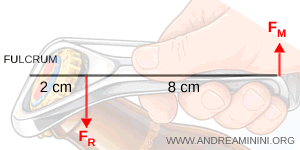
Un ouvre-bouteille de longueur totale 10 cm est utilisé pour retirer le bouchon métallique d'une bouteille.
La distance entre le point d'appui et le point de contact avec le bouchon est de 2 cm, et le bouchon exerce une force résistante de 100 N.
Quelle force motrice doit être appliquée à l'extrémité libre de l'ouvre-bouteille?

Pour simplifier l'analyse, on introduit un repère cartésien \( xy \), en faisant coïncider l'axe \( x \) avec l'axe longitudinal de l'ouvre-bouteille.
L'équilibre du levier impose l'égalité des moments des forces par rapport au point d'appui:
$$ b_R F_R = b_M F_M $$
Les données numériques sont $ b_R = 2 \ \text{cm} = 0.02 \ \text{m} $, $ b_M = (10 - 2) \ \text{cm} = 0.08 \ \text{m} $ et $ F_R = 100 \ \text{N} $.
$$ (0.02 \ \text{m}) \cdot (100 \ \text{N}) = (0.08 \ \text{m}) \cdot F_M $$
Après simplification:
$$ 0.02 \cdot (100 \ \text{N}) = 0.08 \cdot F_M $$
En résolvant pour la force motrice:
$$ F_M = \frac{0.02 \cdot (100 \ \text{N})}{0.08} = 25 \ \text{N} $$
Il faut donc appliquer à l'extrémité de l'ouvre-bouteille une force d'au moins 25 N pour retirer le bouchon.
Dans la pratique, une force légèrement supérieure est nécessaire afin de compenser les frottements, les déformations élastiques et les autres pertes mécaniques.
Et ainsi de suite.