Centre de masse

Le centre de masse est le point où l’on peut considérer que la masse totale d’un objet ou d’un système est concentrée. Cette idée, très simple en apparence, permet d’analyser son mouvement et les forces qui agissent sur lui de manière beaucoup plus directe.

Bien qu’il s’agisse d’une notion abstraite, elle joue un rôle essentiel en mécanique. En assimilant un objet étendu à une particule placée en son centre de masse, on peut étudier des situations complexes tout en conservant l’essentiel de leur comportement physique.

Le centre de masse se comporte comme si toutes les forces extérieures s’y appliquaient directement. Comprendre ce point revient donc à comprendre la translation globale de l’objet ou du système étudié.

Pour un corps rigide, on modélise la translation comme celle d’une particule située au centre de masse. Cette simplification rend les calculs plus rapides et évite de s’enliser dans les détails.

Comment déterminer le centre de masse?

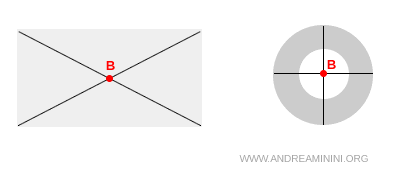
Sa position dépend entièrement de la manière dont la masse est distribuée à l’intérieur de l’objet. Dans les corps homogènes ou symétriques, il coïncide avec le centroïde, le point d’équilibre géométrique.

 

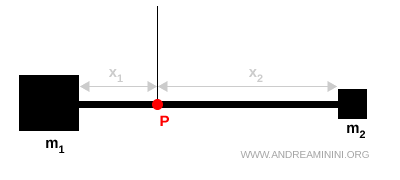
Voici un exemple concret. Une barre rigide porte deux masses, $m_1$ et $m_2$, placées à ses extrémités et suspendues en un point P. Elle reste horizontale lorsque les moments de force autour de P sont équilibrés.

$$ m_1 x_1 = m_2 x_2 $$

Lorsque cette condition est remplie, le point P correspond au centre de masse du système.

Remarque. Dans cet exemple, la masse propre de la barre est négligée. Si elle devait être prise en compte, son poids contribuerait lui aussi aux moments.

Pour les objets de forme irrégulière, il existe une méthode simple et efficace. On les suspend en deux points différents et on trace les verticales correspondantes.

Par exemple, en suspendant une raquette de tennis au point \( P_1 \) et en la laissant se stabiliser, on sait que le centre de masse se situe quelque part sur la verticale \( r_1 \).

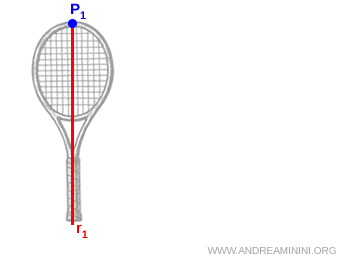
Remarque. À l’équilibre, le moment résultant est nul. La raquette reste alors immobile.

En répétant l’opération depuis un second point \( P_2 \), on obtient une deuxième verticale \( r_2 \).

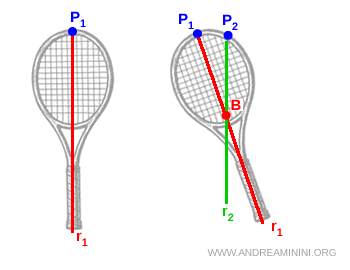
L’intersection de ces deux droites définit un point unique \( B \), qui est le centre de masse de la raquette.

Un exemple pratique

Imaginons maintenant une caisse de 10 kg posée sur un plan incliné.

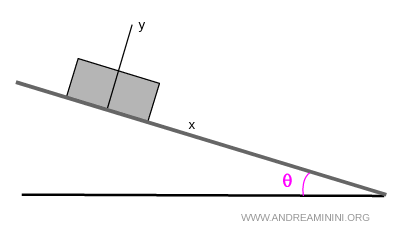
Trois forces principales agissent sur elle: le poids, la réaction normale et le frottement. Pour comprendre son comportement, il suffit de considérer que ces forces s’appliquent toutes en un point unique, le centroïde \( C \).

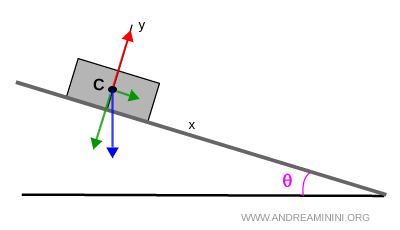
Cette représentation permet d’identifier rapidement les composantes des forces et de visualiser comment elles s’additionnent pour produire le mouvement.

Remarque. Cette simplification est valide si la masse est répartie uniformément. Dans le cas contraire, il faut utiliser le véritable centre de masse défini par la distribution réelle de la masse.

Exemple 2

Considérons deux masses fixées sur une barre horizontale: 2 kg à 0 m et 3 kg à 4 m.

On a donc $m_1 = 2 \ kg$ et $m_2 = 3 \ kg$ pour les positions $x_1 = 0 \ m$ et $x_2 = 4 \ m$.

Le centre de masse se calcule à l’aide de la formule générale:

$$ x_{cm} = \frac{ m_1 x_1 + m_2 x_2 }{ m_1 + m_2 } $$

$$ x_{cm} = \frac{2 \cdot 0 + 3 \cdot 4}{2 + 3} = \frac{12}{5} = 2.4 \, \text{m}
$$

On obtient ainsi un résultat cohérent avec l’intuition: le centre de masse se situe du côté de la masse la plus importante.

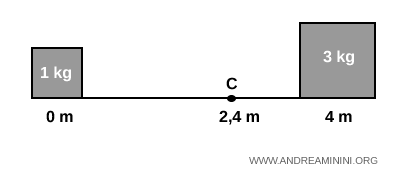
Une fois le centre de masse connu, on peut analyser le mouvement du système en le traitant comme une particule unique. Ce principe est largement utilisé dans les problèmes de dynamique.