Moment angulaire

De quoi dépend le moment angulaire ?

Il est déterminé par :

• la position $ \vec{r} $ du corps par rapport au point de référence $ O $
• sa quantité de mouvement linéaire $ \vec{p} = m \vec{v} $
• l’orientation du mouvement par rapport au vecteur position

Par exemple, dans un mouvement circulaire non uniforme, un corps décrit une trajectoire circulaire dont la vitesse tangentielle varie avec le temps.

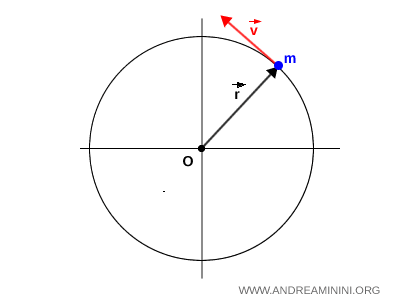
Dans ce cas, la distance $ r $ entre le corps et le centre de rotation $ O $ reste constante. Si la masse $ m $ du corps est également fixe, le moment angulaire est directement proportionnel à la vitesse tangentielle $ \vec{v} $.

Remarque. Un corps en mouvement rectiligne peut lui aussi posséder un moment angulaire, à condition que sa trajectoire ne passe pas par le point de référence $ O $. Dans ce cas, le vecteur position $\vec{r}$ par rapport à $ O $ évolue au cours du temps.

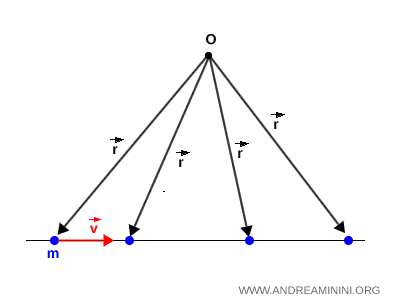
En revanche, si le mouvement rectiligne traverse exactement $ O $, le moment angulaire reste nul à tout instant.

La valeur du moment angulaire dépend de l’angle $ \theta $ entre $ \vec{r} $ et $ \vec{v} $ :

$$ L = mrv \cdot \sin \theta $$

Cette valeur peut varier entre deux extrêmes :

• Lorsque $ \theta = 90^\circ $, le moment angulaire atteint sa valeur maximale $ L = mrv $, car $ \vec{r} $ et $ \vec{v} $ sont perpendiculaires.
• Lorsque $ \theta = 0^\circ $ ou $ \theta = 180^\circ $, le moment angulaire s’annule $ L=0 $, car $ \vec{r} $ et $ \vec{v} $ sont parallèles.

De manière générale, le moment angulaire dépend de plusieurs facteurs, notamment de la masse du corps, de sa position perpendiculaire par rapport à l'axe de rotation, de sa vitesse tangentielle et du système de référence choisi pour décrire le mouvement.

Il est important de noter que le moment angulaire varie dès que la position du corps change par rapport au point $ O $. Cela signifie qu'il ne s'agit pas d'une propriété intrinsèque du corps, mais d'une grandeur liée au mouvement et au référentiel adopté.

Un exemple concret

Considérons un athlète qui se prépare au lancer de marteau.

Le marteau a une masse $m = 7{,}26\,\text{kg}$ et est attaché à un câble de longueur $r = 1{,}20\,\text{m}$.

Lorsque l’athlète effectue ses rotations, le marteau décrit un cercle horizontal autour du point de prise, qui joue le rôle de centre de rotation. Au cours de cette phase, il augmente progressivement la vitesse tangentielle du marteau.

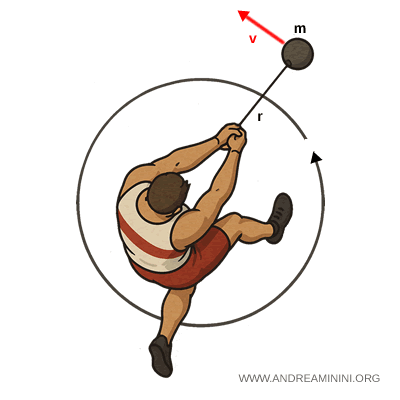
Au moment du lâcher, si la vitesse tangentielle est $v = 28{,}0\,\text{m/s}$, le moment angulaire par rapport au centre de rotation est donné par :

$$ L = m r v $$

En remplaçant les valeurs :

$$ L = (7{,}26\,\text{kg}) \cdot (1{,}20\,\text{m}) \cdot (28{,}0\,\text{m/s}) $$

$$ L \approx 243{,}94\,\text{kg·m}^2/\text{s} $$

Ainsi, au moment du lâcher, le marteau possède un moment angulaire de $ L \approx 243{,}94\,\text{kg·m}^2/\text{s} $.

Ce résultat dépend de trois facteurs essentiels :

• La masse du marteau : plus elle est grande, plus $L$ est élevé.
• Le rayon : plus le bras de levier est long, plus $L$ croît.
• La vitesse tangentielle : c’est le facteur décisif, celui que l’athlète contrôle directement pendant le lancer.

Si, par exemple, l’athlète lâchait le marteau à la moitié de cette vitesse, $v = 14{,}0\,\text{m/s}$, le moment angulaire serait réduit à :

$$ L = 7{,}26 \cdot 1{,}20 \cdot 14{,}0 = 121{,}968 \approx 121{,}97\,\text{kg·m}^2/\text{s} $$

Cela signifie qu’il faudrait exercer beaucoup moins de force pour freiner ou modifier ce mouvement de rotation autour du point d’appui.

Remarque. Dans le lancer de marteau, la masse $ m $ et le rayon $ r $ sont constants. Dans ces conditions, le moment angulaire est directement proportionnel à la vitesse tangentielle $ v $. Autrement dit : plus le marteau tourne vite, plus il est difficile à arrêter. Toutefois, une analyse plus précise doit aussi tenir compte des variations du rayon effectif dues aux déplacements de l’athlète et à l’extension des bras, qui modifient $ r $ et, par conséquent, le moment angulaire.

Loi de conservation du moment angulaire

Si aucun couple extérieur n’agit sur un système, son moment angulaire total reste constant.

Ce principe sous-tend une très large gamme de phénomènes physiques.

Il explique, par exemple, pourquoi un patineur accélère sa rotation en repliant les bras ou pourquoi les satellites et les planètes conservent des orbites stables.

En définitive, le moment angulaire dépend de la masse du corps, de la composante perpendiculaire de sa position par rapport à l’axe de rotation, de sa vitesse tangentielle et du système de référence adopté.

Le moment angulaire de la Terre

La dynamique de la Terre dans l'espace repose sur deux formes principales de moment angulaire. Chacune correspond à un mouvement bien précis et joue un rôle clé dans la stabilité de notre planète à long terme.

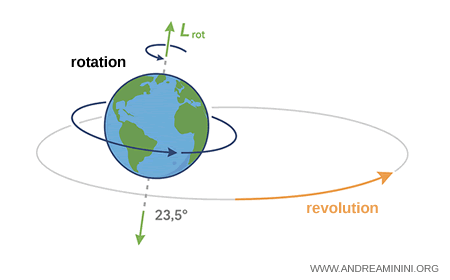
• Moment angulaire de rotation
  La Terre tourne sur elle-même en environ 24 heures. Ce mouvement génère un moment angulaire qui dépend de sa masse, de son rayon, de la façon dont cette masse est répartie et de la vitesse angulaire $ \omega $. Ce moment de rotation contribue à maintenir l'axe terrestre stable dans le temps, assurant ainsi la continuité du rythme jour-nuit.

  Note. Pour un corps rigide, le moment angulaire de rotation se calcule avec $$ L_{\text{rot}} = I  \omega $$ où $ I $ est le moment d'inertie et $ \omega $ la vitesse angulaire. Dans le cas d'une sphère légèrement aplatie comme la Terre, on adopte souvent l'approximation $$ I \approx \frac{2}{5} M R^2 $$ et $$ \omega = \frac{2\pi}{T_{\text{rot}}} $$ avec $ T_{\text{rot}} \approx 24,\text{h} $.

• Moment angulaire orbital
  La Terre tourne également autour du Soleil, un cycle d'environ 365 jours. Ce mouvement engendre un second moment angulaire, déterminé par la masse terrestre, la distance moyenne au Soleil et la vitesse orbitale. Il joue un rôle fondamental dans la stabilité de l'orbite sur de longues durées. Pour un corps en révolution, on utilise $$  L_{\text{orb}} = m v r $$  et, sous forme vectorielle, $$ \mathbf{L}_{\text{orb}} = \mathbf{r} \times \mathbf{p} $$. Ici, $ m $ est la masse de la Terre, $ v $ sa vitesse orbitale et $ r $ la distance moyenne Terre-Soleil.

  Note. Comme le mouvement orbital vérifie $ v = \omega_{\text{orb}} r $, on peut reformuler le moment angulaire orbital sous la forme $$ L_{\text{orb}} = m, r^2, \omega_{\text{orb}} $$ avec $ \omega_{\text{orb}} = \frac{2\pi}{T_{\text{orb}}} $ et $ T_{\text{orb}} \approx 365,\text{giorni} $.

Dans les deux situations, le principe de conservation du moment angulaire est central. C'est lui qui permet à la Terre de conserver une orbite stable et une orientation quasi constante de son axe au cours du temps.

Et ainsi de suite.