Moment d’un couple de forces
Le moment d’un couple de forces mesure la capacité de deux forces à faire tourner un système. On le calcule à partir de la relation $$ M = F \cdot d $$ où $ F $ est l’intensité de l’une des forces et $ d $ la distance entre leurs lignes d’action.
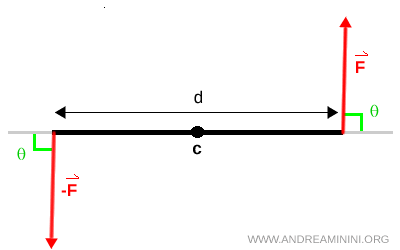
Lorsque les forces ne sont pas perpendiculaires à la ligne qui relie leurs points d’application, on utilise la formule plus générale $$ M = F \cdot d \cdot \sin\theta $$ où $ \theta $ représente l’angle entre la force et la ligne de liaison.
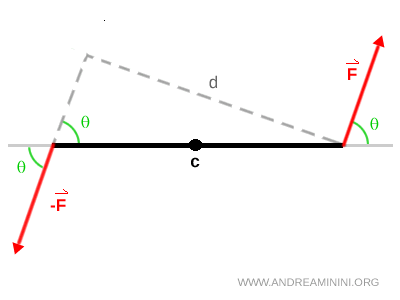
Un couple est constitué de deux forces parallèles, de même intensité et de sens opposés. Ce système ne produit pas de translation, mais uniquement un mouvement de rotation du solide auquel il est appliqué. C’est l’une des notions fondamentales pour comprendre le fonctionnement de leviers, de mécanismes et de dispositifs de commande, comme les vannes ou les volants.
La distance entre les lignes d’action est appelée le bras du couple. Même si les deux forces se compensent en valeur, elles restent capables de générer une rotation car elles s’appliquent sur des côtés opposés du solide. On obtient alors un moment net, sans déplacement du centre de masse.
Remarque. La convention de signe est la même que pour le moment d’une force. Le moment est positif ( $ M > 0 $ ) si la rotation est antihoraire et négatif ( $ M < 0 $ ) si elle est horaire. Si $ M = 0 $ aucune rotation ne se produit.
Exemple 1. Action sur une vanne hydraulique
Imaginons une vanne hydraulique manoeuvrée à deux mains. La main gauche exerce une force vers le bas et la main droite une force vers le haut, chacune d’intensité $ F = 8 \ N $.
Les deux forces sont appliquées à $ 10 \ cm $ du centre de rotation, perpendiculairement au bras de levier.
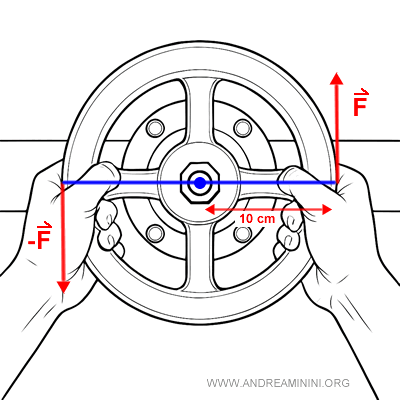
Le couple résultant est donc capable de faire tourner la vanne. On calcule le moment associé au couple.
$$ M = F \cdot d $$
La distance totale entre les forces est de $ 10 \ cm + 10 \ cm = 20 \ cm $.
$$ M = F \cdot ( 20 \ cm ) $$
En mètres.
$$ M = F \cdot ( 0.2 \ m ) $$
En considérant l’action d’une seule force.
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) $$
$$ M = 1.6 \ Nm $$
Le couple ainsi appliqué produit un moment de 1.6 Nm.
Exemple 2. Cas d’un angle d’application
Reprenons la même situation, mais cette fois les forces sont appliquées avec un angle de 110° par rapport au bras de levier.
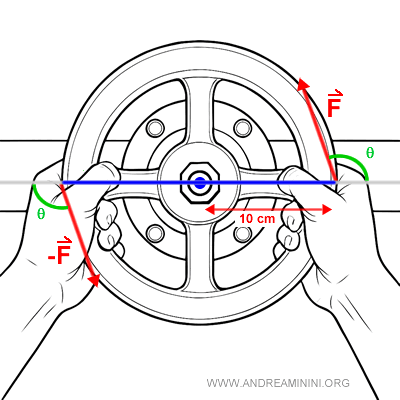
Les intensités et les distances restent inchangées. Chaque main applique $ 8 \ N $ à $ 10 \ cm $ du centre. Le calcul devient alors.
$$ M = F \cdot d \cdot \sin\theta $$
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot \sin 110° $$
Grâce à l’identité $ \sin \theta = \sin (180° - \theta ) $.
$$ \sin 110° = \sin 70° $$
On obtient.
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot \sin 70° $$
$$ M = ( 8 \ N ) \cdot ( 0.2 \ m ) \cdot 0.94 $$
$$ M \approx 1.50 \ Nm $$
Le moment est légèrement plus faible dans ce cas, car les forces ne sont plus perpendiculaires au bras d’action. Cette méthode de calcul s’étend à toutes les configurations géométriques où l’angle doit être pris en compte.