Pression
La pression (p) est une grandeur physique qui décrit l’intensité avec laquelle une force s’exerce sur une surface. Elle est définie comme le rapport entre la composante de la force perpendiculaire à la surface, $ F_{\perp} $, et l’aire $ A $ sur laquelle cette force est appliquée. $$ p = \frac{F_{\perp}}{A} $$
Pour qu’il y ait pression, la force doit agir perpendiculairement à la surface. Si la force est inclinée, seule sa composante normale contribue à la pression.
Lorsque la force est entièrement perpendiculaire à la surface, l’expression se simplifie et devient :
$$ p = \frac{F}{A} $$
Cette relation permet de comprendre immédiatement un point clé. La pression augmente lorsque la force appliquée augmente, et elle diminue lorsque la force est répartie sur une surface plus grande.
Il est ainsi possible de doubler la pression de deux manières équivalentes : soit en doublant la force, soit en divisant l’aire par deux. Dans les deux cas, le résultat est le même.
$$ 2p = \frac{2F}{A} = \frac{F}{\frac{A}{2}} $$
On en déduit qu’à force identique, une surface de contact plus petite entraîne une pression plus élevée.
Un exemple simple de la vie quotidienne illustre bien cette idée. Lorsque l’on appuie sur un ballon avec le doigt, la pression reste modérée, car la force se répartit sur une surface de contact relativement large. Le ballon se déforme, mais ne se rompt pas. En revanche, si l’on exerce la même force avec une épingle, la pression devient très élevée, puisque la force est concentrée sur une aire extrêmement réduite, et le ballon éclate.

Autrement dit, l’effet d’une force appliquée à une surface ne dépend pas uniquement de sa valeur, mais aussi de la surface sur laquelle elle est répartie. C’est ce principe qui explique pourquoi un ballon résiste à la pression d’un doigt, alors qu’il éclate très facilement lorsqu’on le touche avec une épingle.
La pression est une notion fondamentale pour comprendre la manière dont les forces se transmettent dans les solides et dans les fluides. Elle intervient dans de nombreux phénomènes physiques du quotidien comme dans un grand nombre d’applications techniques.
L’unité de mesure de la pression
La pression est une grandeur scalaire, car elle est entièrement décrite par une valeur numérique et par une unité de mesure.
Dans le Système international d’unités (SI), l’unité de pression est le pascal (Pa).
$$ 1 \ \text{Pa} = 1 \ \frac{\text{N}}{\text{m}^2} $$
Concrètement, une pression de 1 pascal correspond à l’action d’une force de 1 newton répartie uniformément sur une surface de 1 mètre carré.
Cette unité porte le nom du physicien français Blaise Pascal (1623-1662), dont les travaux ont été déterminants pour la compréhension de la pression et pour le développement de la mécanique des fluides.
Remarque. Du point de vue de l’analyse dimensionnelle, la pression est le rapport entre une force et une aire, c’est-à-dire une longueur (L) élevée au carré : \[ p = \frac{[F]}{[L^2]} \] La force \( F \) a pour dimensions \([M \cdot L \cdot T^{-2}] \), correspondant à une masse multipliée par une accélération, tandis que l’aire a pour dimensions \([L^2] \). En remplaçant dans l’expression, on obtient : \[ [p] = \frac{[M \cdot L \cdot T^{-2}]}{[L^2]} = [M \cdot L^{-1} \cdot T^{-2}] \] Cette expression correspond à la dimension physique du pascal et met en évidence la signification physique de la pression.
La pression se mesure à l’aide d’instruments appelés manomètres ou appareils de mesure de la pression. Il en existe différents types, adaptés à la nature du fluide étudié et à la plage de pressions à mesurer, aussi bien pour les gaz que pour les liquides, et pour des situations de basse comme de haute pression.
Exemple de calcul
On considère ici un calcul simple de pression exercée sur la surface d’un ballon lorsqu’une force de \( 2.6 \ \text{N} \) est appliquée. Deux situations, très différentes du point de vue physique, sont comparées :
- a) le contact avec un doigt, dont l’aire de contact est \( 1.1 \cdot 10^{-4} \ \text{m}^2 \)
- b) le contact avec une épingle, dont la pointe possède une aire de \( 2.1 \cdot 10^{-7} \ \text{m}^2 \)
On sait également que le ballon éclate lorsque la pression atteint la valeur critique \( 4.1 \cdot 10^{5} \ \text{Pa} \). L’objectif est donc de déterminer la force minimale nécessaire pour provoquer la rupture dans chacun des deux cas.
a] Pression exercée par le doigt
Une force \( F = 2.6 \ \text{N} \) est appliquée sur une aire \( A = 1.1 \cdot 10^{-4} \ \text{m}^2 \), correspondant à la surface de contact du doigt.
La pression exercée par le doigt se calcule directement à partir de la définition de la pression :
\[ p = \frac{F}{A} = \frac{2.6 \ \text{N}}{1.1 \cdot 10^{-4} \ \text{m}^2} \]
En rappelant que le pascal est défini par $ Pa = \frac{\text{N}}{\text{m}^2} $, le calcul conduit à :
\[ p \approx 2.36 \cdot 10^{4} \ \text{Pa} \]
La pression obtenue est relativement faible, car la force appliquée est répartie sur une surface de contact assez grande.
b] Pression exercée par l’épingle
Dans ce second cas, la même force \( F = 2.6 \ \text{N} \) est appliquée sur une aire beaucoup plus petite, \( A = 2.1 \cdot 10^{-7} \ \text{m}^2 \), correspondant à la pointe de l’épingle.
La pression exercée par l’épingle est alors donnée par :
\[ p = \frac{F}{A} = \frac{2.6 \ \text{N}}{2.1 \cdot 10^{-7} \ \text{m}^2} \]
En effectuant le calcul, on obtient :
\[ p \approx 1.24 \cdot 10^{7} \ \text{Pa} \]
La pression est ici plusieurs centaines de fois plus élevée, car la même force est concentrée sur une région extrêmement réduite.
c] Force minimale nécessaire pour rompre le ballon avec une épingle
La pression de rupture du ballon étant \( p = 4.1 \cdot 10^{5} \ \text{Pa} \), la force minimale nécessaire s’obtient en isolant la force dans la relation de définition de la pression :
\[ F = pA \]
En remplaçant par les valeurs numériques, avec l’aire de la pointe de l’épingle \( A = 2.1 \cdot 10^{-7} \ \text{m}^2 \), on obtient :
\[ F = (4.1 \cdot 10^{5} \ \text{Pa}) \cdot (2.1 \cdot 10^{-7} \ \text{m}^2) \]
En rappelant que $ Pa = \frac{\text{N}}{\text{m}^2} $ :
\[ F = (4.1 \cdot 10^{5} \ \frac{\text{N}}{\text{m}^2}) \cdot (2.1 \cdot 10^{-7} \ \text{m}^2) \]
\[ F = (4.1 \cdot 10^{5} \ \text{N}) \cdot (2.1 \cdot 10^{-7}) \]
\[ F = 8.61 \cdot 10^{-2} \ \text{N} \]
La force minimale requise est donc :
\( F_{\min} \approx 0.086 \ \text{N} \)
Une force très faible suffit ainsi à provoquer la rupture lorsqu’elle est appliquée sur une surface extrêmement petite.
d] Force minimale nécessaire pour rompre le ballon avec un doigt
Le raisonnement est identique. À partir de la relation \( p = \frac{F}{A} \), la force s’exprime sous la forme :
\[ F = pA \]
La pression de rupture est toujours \( p = 4.1 \cdot 10^{5} \ \text{Pa} \), mais l’aire de contact du doigt vaut maintenant \( A = 1.1 \cdot 10^{-4} \ \text{m}^2 \).
\[ F = (4.1 \cdot 10^{5} \ \text{Pa}) \cdot (1.1 \cdot 10^{-4} \ \text{m}^2) \]
En utilisant l’expression du pascal :
\[ F = (4.1 \cdot 10^{5} \ \frac{\text{N}}{\text{m}^2}) \cdot (1.1 \cdot 10^{-4} \ \text{m}^2) \]
\[ F = (4.1 \cdot 10^{5} \ \text{N}) \cdot (1.1 \cdot 10^{-4}) \]
En combinant les puissances de dix \( 10^{5} \cdot 10^{-4} = 10^{1} \) et les coefficients numériques \( 4.1 \cdot 1.1 = 4.51 \), on obtient :
\[ F = 4.51 \cdot 10^{1} \ \text{N} \]
La force minimale nécessaire est donc :
\[ F_{\min} \approx 45 \ \text{N} \]
Ce résultat montre clairement que, pour une même pression critique, la force requise dépend fortement de l’aire sur laquelle elle est appliquée. Plus la surface de contact est petite, plus la pression générée est élevée à force égale.
Pression dans les fluides
La pression dans un fluide correspond à la force qu'un fluide exerce, par unité de surface, sur les parois du récipient qui le contient, sur les corps immergés et sur les zones voisines du fluide lui-même.
Cette pression s'exerce toujours selon la direction normale, c'est-à-dire perpendiculairement à la surface considérée. Cela vaut aussi bien pour la paroi d'un récipient que pour la surface d'un objet plongé dans le fluide ou pour une surface idéale, purement imaginaire, située à l'intérieur du fluide.
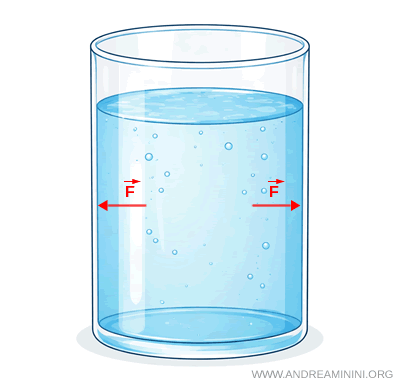
Lorsqu'un fluide est en équilibre, autrement dit lorsqu'il est au repos, la pression présente une propriété essentielle: en tout point du fluide, elle a la même valeur dans toutes les directions.
Pour mieux comprendre ce point, imaginons un point quelconque à l'intérieur d'un fluide au repos et une petite surface imaginaire passant par ce point. Sur chacune des faces de cette surface agissent des forces de pression perpendiculaires aux faces elles-mêmes. Ces forces ont la même intensité mais des sens opposés, ce qui fait qu'elles se compensent exactement.

Si l'on change l'orientation de la surface imaginaire, la direction de la force exercée par le fluide change également. En revanche, la valeur de la pression reste la même. Cela montre que la pression ne dépend pas de l'orientation de la surface et qu'elle est identique dans toutes les directions de l'espace.
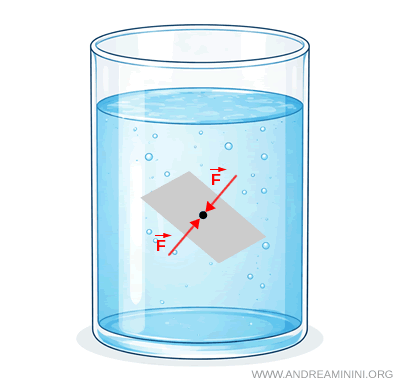
Remarque. La pression n'étant associée à aucune direction privilégiée, elle n'est pas une grandeur vectorielle. La pression est une grandeur scalaire.
Autrement dit, en chaque point d'un fluide en équilibre s'exercent des forces de pression égales et opposées dans toutes les directions.
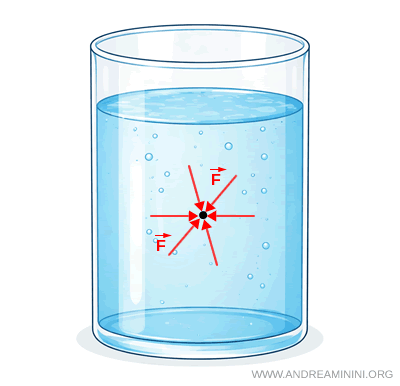
Si cette condition n'était pas respectée, les forces ne se compenseraient plus. Une force résultante apparaîtrait et le fluide se mettrait alors en mouvement.
C'est pourquoi l'isotropie de la pression est une condition indispensable pour qu'un fluide puisse rester en équilibre mécanique.
Et ainsi de suite.