Correspondance biunivoque entre vecteurs et points du plan

Tout point $ P $ du plan, défini par ses coordonnées $ (x, y) $, peut être associé de manière unique au vecteur $ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} $. Ce vecteur, appelé vecteur de position, a pour origine le point $ O $ et pour extrémité le point $ P $. La réciproque est également vraie.
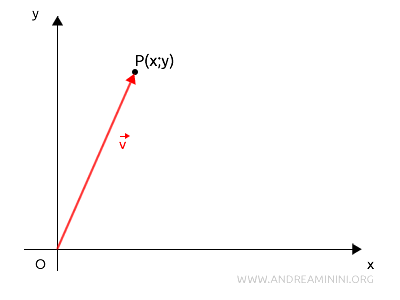
correspondance entre vecteur et point dans le plan

Autrement dit, il existe une correspondance parfaitement biunivoque entre les points du plan et les vecteurs de l’espace vectoriel $ \mathbb{R}^2 $.

Cela signifie que les points du plan et les vecteurs de $ \mathbb{R}^2 $ offrent deux formulations équivalentes d’un même concept : un point peut être représenté par un vecteur, et un vecteur détermine un point unique.

Cette correspondance dépend du choix d’un origine $ O $, qui sert de référence pour définir les vecteurs de position.

La relation entre points du plan et vecteurs de $ \mathbb{R}^2 $ est biunivoque pour les raisons suivantes :

Chaque point du plan correspond à un unique vecteur de position
Tout point $ P(x, y) $ se représente de manière univoque par le vecteur $ \vec{OP} = \begin{pmatrix} x \\ y \end{pmatrix} $.
Chaque vecteur correspond à un point unique
Tout vecteur $ \begin{pmatrix} x \\ y \end{pmatrix} $ détermine un seul point $ P(x, y) $ du plan.

Exemple

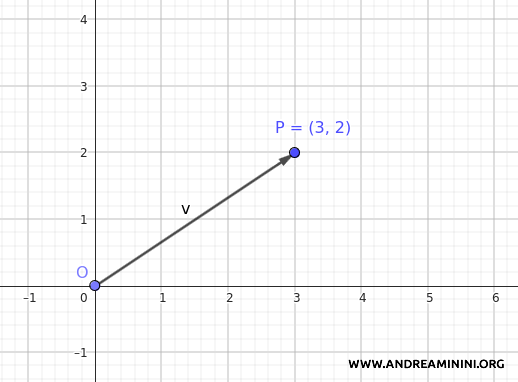
Par exemple, si un point du plan a pour coordonnées $ P(3, 2) $, son vecteur de position associé est :

$$ \vec{OP} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $$

Réciproquement, le vecteur $ \vec{v} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} $ correspond exactement au point $ P(3, 2) $ du plan.

exemple pratique de correspondance entre vecteur et point

Et ainsi de suite.