Addition de deux vecteurs

Lorsque l’on travaille avec deux vecteurs, par exemple v et w, on peut calculer leur somme v+w de plusieurs façons. La plus répandue est la méthode du parallélogramme. Une autre consiste à additionner directement les coordonnées des deux vecteurs. Formellement : $$ \vec{v} + \vec{w} = \begin{pmatrix} v_1 \\ v_2 \\ \vdots \\ v_n \end{pmatrix} + \begin{pmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{pmatrix} = \begin{pmatrix} v_1 + w_1 \\ v_2 + w_2 \\ \vdots \\ v_n + w_n \end{pmatrix} $$

Quel que soit le procédé utilisé, le résultat est toujours le même : la somme de v et w donne un nouveau vecteur.

Ce vecteur est appelé le vecteur somme.

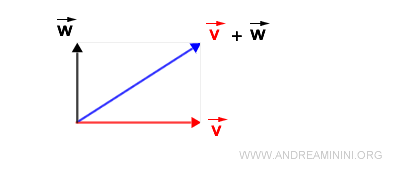
Méthode du parallélogramme

Lorsqu’on représente les vecteurs dans le plan, la méthode du parallélogramme offre une interprétation géométrique particulièrement intuitive de leur somme.

Considérons deux vecteurs v et w, issus d’un même point O mais orientés différemment.

• Le vecteur v s’étend de O jusqu’au point A et définit sa norme.
• Le vecteur w s’étend de O jusqu’au point B.

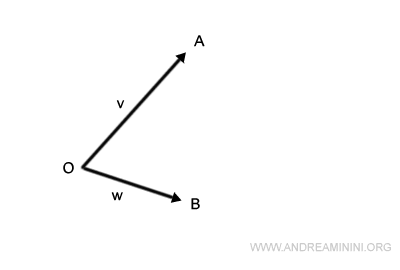
Comment déterminer leur somme ?

On commence par translater le segment OA de façon que son origine coïncide avec le point B.

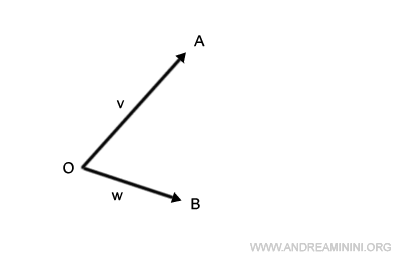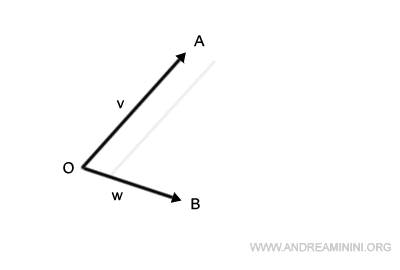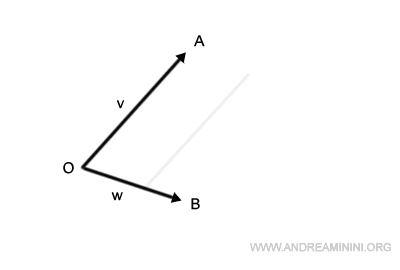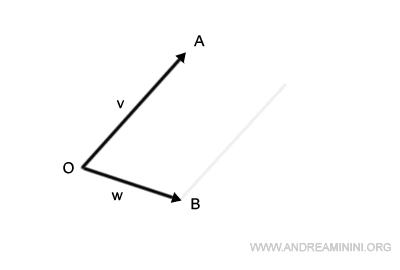
De la même manière, on déplace le segment OB pour qu’il parte du point A.

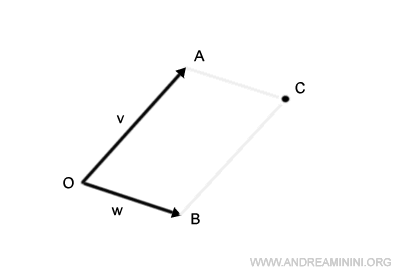
Leurs prolongements se coupent en un point C.

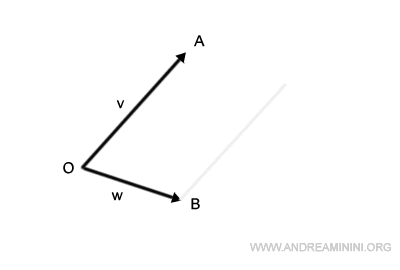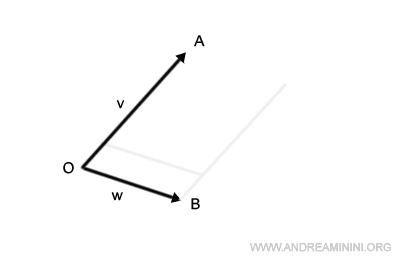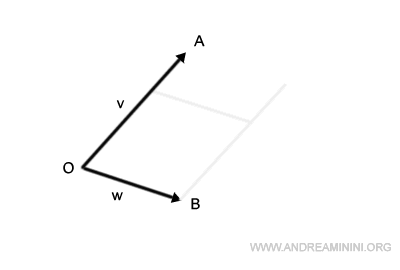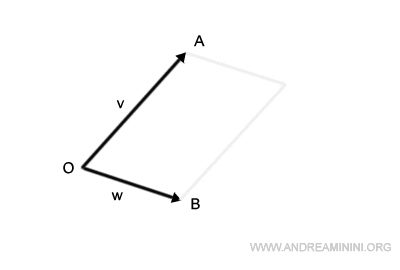
On obtient ainsi le parallélogramme OACB.

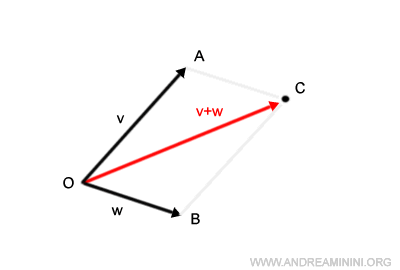
Le segment reliant O à C représente la somme des vecteurs v+w.

Si les deux vecteurs sont colinéaires, leurs longueurs se placent sur une même droite. Le parallélogramme devient alors dégénéré et ne permet plus de visualiser la somme. Dans ce cas, on utilise le plus souvent la méthode du point médian.

Calcul vectoriel : un exemple

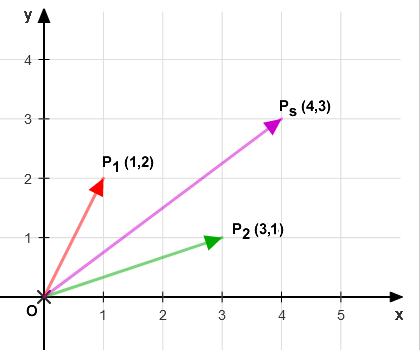
Dans l’espace vectoriel V=R², considérons deux vecteurs précis :

$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ $$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$$

Ces vecteurs se représentent dans le plan cartésien (x,y) par les segments dirigés OP₁ et OP₂, allant de l’origine vers les points P₁ et P₂.

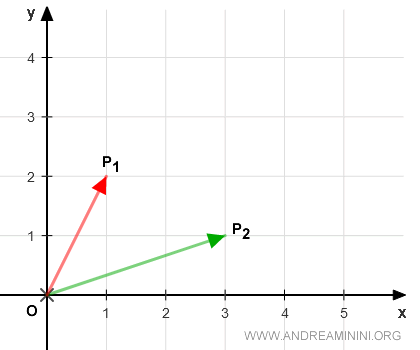
Il faut bien comprendre que tout point du plan correspond à un vecteur d’origine O. Réciproquement, tout vecteur d’origine O est associé à un point unique du plan (x,y). En d’autres termes, points et vecteurs sont deux façons équivalentes de décrire la même réalité géométrique.

Pour additionner OP₁ et OP₂, on applique la méthode du parallélogramme.

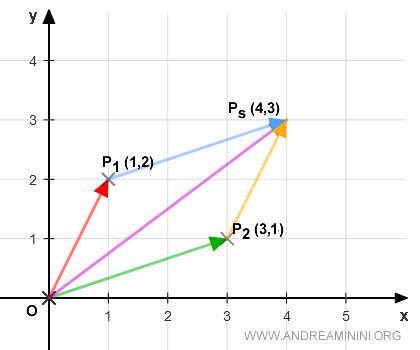
Le vecteur résultant OP₁+OP₂ relie l’origine au point P_s(4,3).

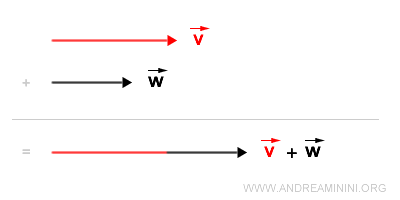
Méthode tête-à-queue

Il existe un autre procédé très intuitif pour additionner des vecteurs : la méthode tête-à-queue. Plutôt que de recourir à un calcul, il suffit de translater un vecteur de manière à placer sa base sur la pointe de l’autre.

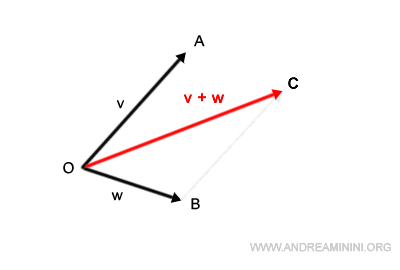
On obtient ainsi directement le vecteur résultant v+w.

Exemple pratique :

Supposons que l’on veuille additionner v et w :

On déplace la base de v jusqu’à la pointe de w.

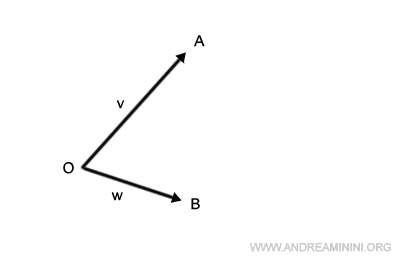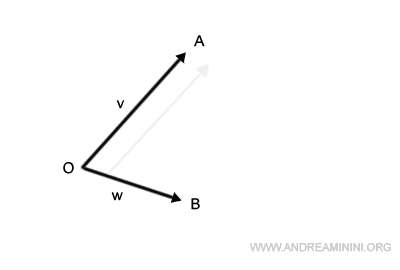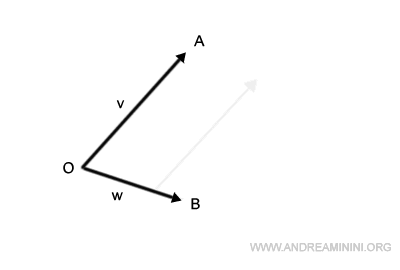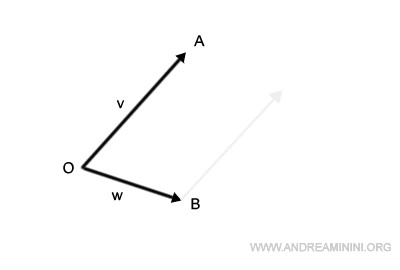
Puis on trace le segment qui relie l’origine O à l’extrémité du vecteur v ainsi déplacé. On obtient alors le vecteur somme v+w.

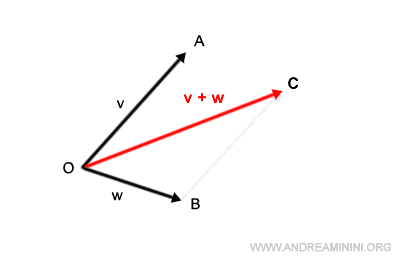
On constate que cette méthode conduit au même résultat que celle du parallélogramme.

De plus, la méthode tête-à-queue est plus directe et se prête bien à l’addition successive de plusieurs vecteurs.

Autre exemple :

Voyons comment additionner trois vecteurs : v, w et z.

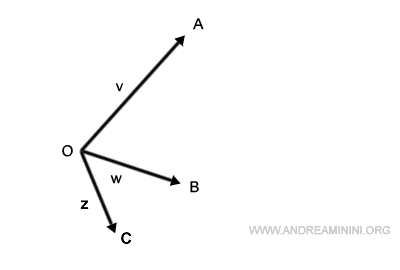
On commence par placer la base de w sur la pointe de v.

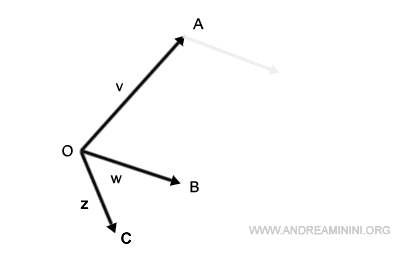
Puis on positionne la base de z à l’extrémité du nouveau vecteur w.

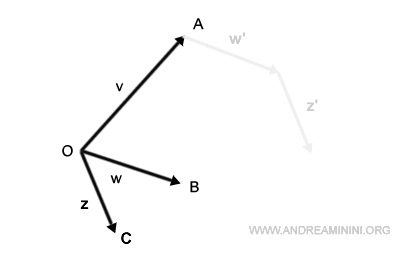
Enfin, en reliant l’origine au point final, on obtient le vecteur résultant v+w+z.

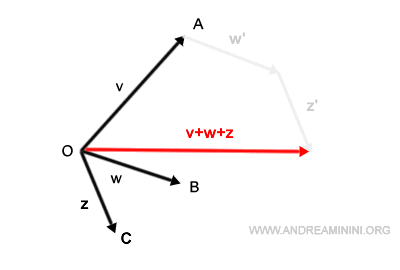
Cette méthode est très pratique pour additionner plusieurs vecteurs géométriquement. Et point essentiel : l’ordre d’addition n’a aucune influence sur le résultat. La somme reste toujours la même.

Par exemple, qu’on additionne d’abord v et w puis z, ou dans un autre ordre, le vecteur résultant v+w+z est identique. La grande force de cette méthode est que la somme est indépendante de l’ordre d’addition.

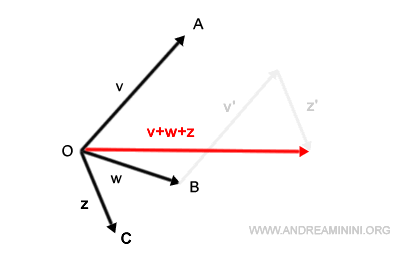
Addition algébrique de vecteurs

Pour déterminer le vecteur résultant, il suffit d’additionner directement les coordonnées (x, y) des deux vecteurs : $$ \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} x_1+x_2 \\ y_1+y_2 \end{pmatrix} $$

Cette méthode purement algébrique s’avère particulièrement efficace dès que l’on travaille avec des vecteurs de dimension supérieure à deux.

Exemple

Reprenons les vecteurs introduits dans l’exemple précédent :

$$ P_1 = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$ $$ P_2 = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$$

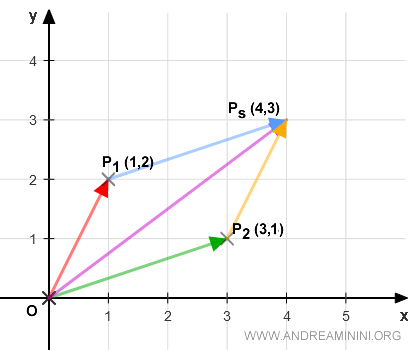
Calculons maintenant la somme algébrique des vecteurs OP₁ et OP₂.

On additionne simplement les coordonnées correspondantes :

$$ OP_S = OP_1 + OP_2 = \begin{pmatrix} 1 \\ 2 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \end{pmatrix} $$

On obtient ainsi le vecteur somme.

Représentons ce vecteur dans le plan cartésien : on constate que la somme conduit naturellement au vecteur OP_s.

Le point P_s correspond exactement au vecteur somme déjà obtenu par la méthode du parallélogramme, ce qui confirme la cohérence entre les deux approches.

Exemple 2

Considérons maintenant deux vecteurs dans un espace tridimensionnel (x, y, z) :

$$ P_1= \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$ $$ P_2 = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \\ 4 \end{pmatrix}$$

Le vecteur somme s’obtient en additionnant chaque composante :

$$ P_1 + P_2 = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} + \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} x_1 + x_2 \\ y_1 + y_2 \\ z_1 + z_2 \end{pmatrix} = \begin{pmatrix} 1 + 3 \\ 2 + 1 \\ 3 + 4 \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 7 \end{pmatrix} $$

Ce procédé est parfaitement général et s’applique à des vecteurs de toute dimension.

Exemple 3

Passons maintenant à un espace de dimension quatre (x₁, x₂, x₃, x₄) :

$$ v = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $$ $$ w = \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix}$$

L’addition composante par composante donne :

$$ v + w = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3 \\ 2+1 \\ 3+4 \\ 4+(-2) \end{pmatrix} = \begin{pmatrix} 4 \\ 3 \\ 7 \\ 2 \end{pmatrix} $$

Le même raisonnement permet d’additionner n’importe quel nombre de vecteurs, quelle que soit la dimension de l’espace.

Exemple 4

Considérons trois vecteurs dans un espace à quatre dimensions :

$$ v_1 = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} $$ $$ v_2 = \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix}$$ $$ v_3 = \begin{pmatrix} -1 \\ 1 \\ 1 \\ 3 \end{pmatrix} $$

Le vecteur somme se calcule en additionnant toutes les composantes :

$$ v_1 + v_2 + v_3 = \begin{pmatrix} 1 \\ 2 \\ 3 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ 1 \\ 4 \\ -2 \end{pmatrix} + \begin{pmatrix} -1 \\ 1 \\ 1 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3+(-1) \\ 2+1+1 \\ 3+4+1 \\ 4+(-2)+3 \end{pmatrix} = \begin{pmatrix} 3 \\ 4 \\ 8 \\ 5 \end{pmatrix} $$

La méthode est systématique et s’applique sans restriction.

Méthode du point médian pour l’addition de vecteurs

Lorsqu’il s’agit d’additionner deux vecteurs colinéaires, la méthode du point médian se révèle très utile. Elle consiste à repérer le milieu M des extrémités des deux vecteurs, puis à doubler le segment OM.

Cette approche est particulièrement pertinente lorsque les vecteurs sont alignés, même si leurs normes sont différentes ou opposées.

À retenir : si les vecteurs sont opposés, la méthode du parallélogramme devient inutilisable car elle produit un parallélogramme dégénéré. Le recours au point médian est alors le plus adapté. Par ailleurs, si les vecteurs sont colinéaires et de même norme, la somme s’obtient immédiatement en additionnant leurs longueurs, sans passer par le point médian.

Démonstration conceptuelle

Dans tout parallélogramme, les diagonales se coupent en leur milieu.

Puisque le segment OC représente la norme du vecteur somme v+w, il suffit de tracer la diagonale AB et d’en déterminer le milieu M.

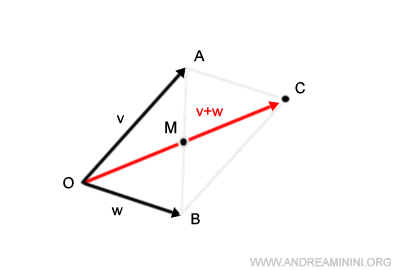
Le point M possède deux propriétés fondamentales :

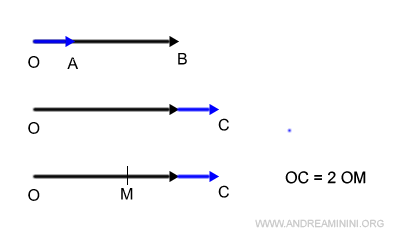
1. Il est équidistant de O et de C : $$ OM = MC $$
2. Le segment OM correspond à la moitié de la norme du vecteur somme : $$ OC = 2 \cdot OM $$

Ces propriétés permettent de calculer avec précision la somme de deux vecteurs colinéaires.

Concrètement, on détermine le milieu des points A et B, ce qui définit le segment OM.

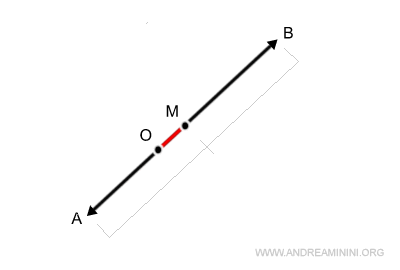
Comme OM représente la moitié de la norme du vecteur somme, il suffit de le doubler pour obtenir 2 OM, c’est-à-dire la norme complète du vecteur somme.

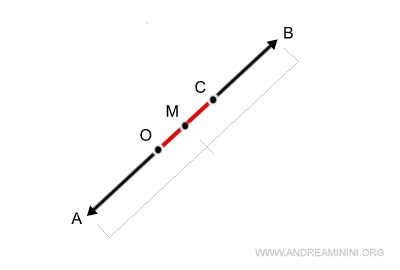
Voici le vecteur somme :

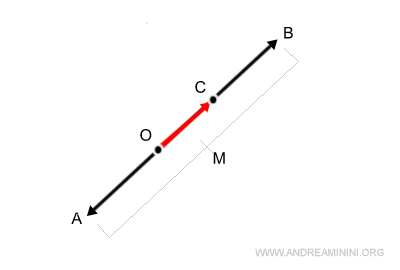
Remarque. Bien que la méthode du point médian puisse s’appliquer à des vecteurs colinéaires de même norme, elle est alors superflue : une simple addition des longueurs suffit. Le calcul du milieu et son doublement n’apportent aucune information supplémentaire dans ce cas.

La portée de l’inégalité triangulaire

Un principe fondamental de l’algèbre vectorielle est l’inégalité triangulaire. Elle affirme que la norme (ou longueur) de la somme de deux vecteurs n’excède jamais la somme de leurs normes respectives : $$ | \vec{v} + \vec{w} | \le |\vec{v}|+|\vec{w}| $$

 

Pourquoi parle-t-on d’« inégalité triangulaire » ?

Le nom provient d’une propriété élémentaire des triangles : dans tout triangle, la somme des longueurs de deux côtés est toujours supérieure à celle du troisième.

Il existe un cas particulier où l’inégalité devient une égalité : lorsque les vecteurs sont parallèles et orientés dans le même sens. Dans ce cas : $$ | \vec{v} + \vec{w} | = |\vec{v}|+|\vec{w}| $$

Le vecteur résultant conserve alors la même direction et le même sens que les vecteurs initiaux.

Et ainsi de suite.