Vecteurs unitaires
Qu’est-ce qu’un vecteur unitaire ?
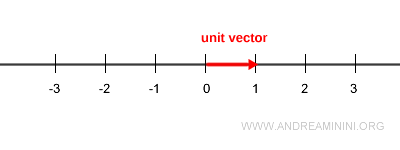
Un vecteur unitaire est un vecteur dont la norme (ou module) vaut exactement 1 et qui indique une direction précise dans l’espace.
Le long d’une même droite, on peut construire une infinité de vecteurs de longueurs différentes, orientés dans un sens ou dans l’autre.
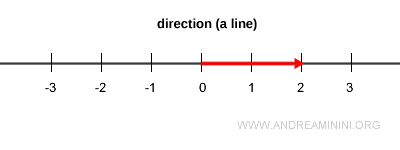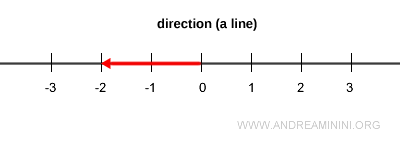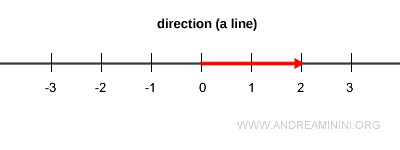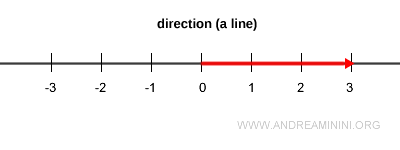
Mais dans chaque direction, un seul vecteur possède une longueur égale à 1 : c’est le vecteur unitaire.
Pourquoi l’appelle-t-on vecteur unitaire ?
Parce que son module est égal à un. Il sert à fixer une direction et un sens le long d’une droite.
À quoi servent les vecteurs unitaires ?
Tout vecteur de même direction peut s’obtenir en multipliant le vecteur unitaire par un nombre réel \( k \).
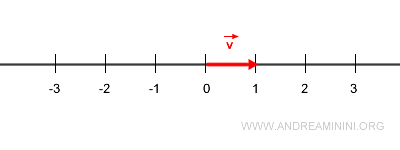
Exemple
Soit \( \vec{v} \) un vecteur unitaire.
Supposons que \( \vec{w} \) soit un vecteur de norme 3.
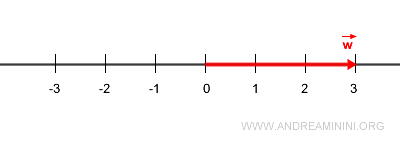
On peut alors écrire :
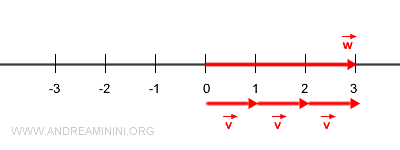
$$ \vec{w} = 3 \cdot \vec{v} $$
Le vecteur obtenu a la même direction que \( \vec{v} \), mais une longueur triple.
Exemple 2
Soit encore \( \vec{v} \) un vecteur unitaire.
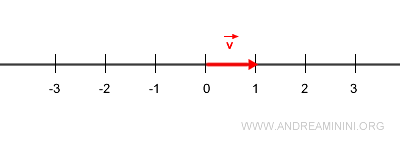
Considérons maintenant un vecteur \( \vec{u} \) de norme 2, orienté en sens inverse.
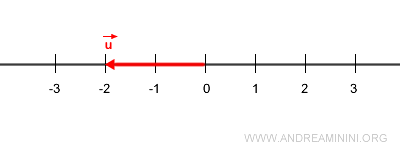
Remarque. La norme de \( \vec{u} \) est 2. On ne peut pas dire que sa norme est -2 : la norme est toujours positive. Le signe négatif n’indique que le sens par rapport au vecteur unitaire.
On a alors :
$$ \vec{u} = -2 \cdot \vec{v} $$
Le facteur négatif inverse la direction du vecteur :
$$ \vec{u} = 2 \cdot (-\vec{v}) $$
Dans ce cas, \( -\vec{v} \) est le vecteur opposé de \( \vec{v} \).
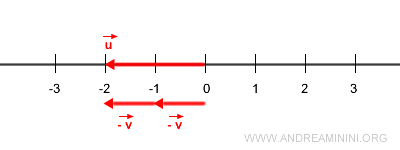
En résumé, une fois connu le vecteur unitaire, on peut engendrer tous les vecteurs situés sur la même droite par simple multiplication scalaire.
Vecteurs unitaires des axes de coordonnées
Tout vecteur de l’espace cartésien tridimensionnel s’écrit comme une combinaison linéaire des vecteurs unitaires dirigés suivant les axes \( x \), \( y \) et \( z \) : $$ \vec{w} = \alpha_1 \cdot \vec{u_x} + \alpha_2 \cdot \vec{u_y} + \alpha_3 \cdot \vec{u_z} $$
Ces vecteurs unitaires se notent en général \( \vec{u_x} \), \( \vec{u_y} \), \( \vec{u_z} \), ou encore avec les notations classiques \( \hat{i} \), \( \hat{j} \), \( \hat{k} \).
Les coefficients \( \alpha_1 \), \( \alpha_2 \) et \( \alpha_3 \) sont des scalaires, c’est-à-dire des nombres réels représentant la projection du vecteur sur chaque axe.
Exemple
En dimension 2, il suffit de prendre \( \vec{u_x} \) et \( \vec{u_y} \).
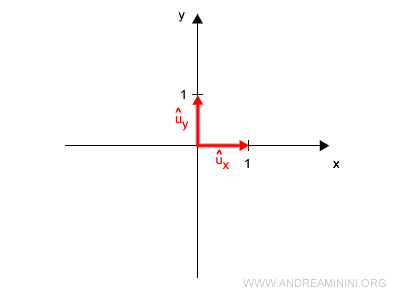
Remarque. Pour plus de clarté, nous utilisons les vecteurs unitaires de la base canonique : $$ \vec{u_x} = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad \vec{u_y} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$ Bien entendu, tout couple de vecteurs linéairement indépendants peut aussi former une base du plan.
La combinaison linéaire de ces vecteurs permet d’exprimer n’importe quel vecteur du plan.
Par exemple, pour construire le vecteur \( \vec{w} = (2,1)^T \) :
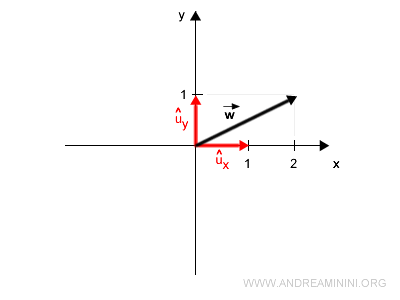
Remarque. L’exposant \( T \) indique la transposée, c’est-à-dire que le vecteur ligne est écrit sous forme de vecteur colonne : $$ \vec{w} = \begin{pmatrix} 2 , 1 \end{pmatrix}^T = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$
On peut alors écrire :
$$ \vec{w} = \alpha_1 \cdot \vec{u_x} + \alpha_2 \cdot \vec{u_y} $$
avec \( \alpha_1 = 2 \) et \( \alpha_2 = 1 \) :
$$ \vec{w} = 2 \cdot \vec{u_x} + 1 \cdot \vec{u_y} $$
En remplaçant les vecteurs unitaires par leur écriture matricielle :
$$ \vec{w} = 2 \cdot \begin{pmatrix} 1 \\ 0 \end{pmatrix} + 1 \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$
Ce qui donne :
$$ \vec{w} = \begin{pmatrix} 2 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 1 \end{pmatrix} $$
Et finalement, en additionnant composante par composante :
$$ \vec{w} = \begin{pmatrix} 2+0 \\ 0+1 \end{pmatrix} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} $$
Ainsi, tout vecteur de l’espace cartésien peut s’exprimer comme une combinaison linéaire des vecteurs unitaires de la base.
Et ainsi de suite.