Vecteur opposé

Le vecteur opposé d’un vecteur $ \vec{v} $ est le vecteur $ -\vec{v} $ qui possède la même direction et la même norme (longueur), mais dont le sens est inverse de celui de \( \vec{v} \).

On obtient le vecteur opposé en multipliant \( \vec{v} \) par le scalaire -1, au moyen de la multiplication scalaire.

Premier exemple

Considérons un vecteur de norme 3.

La droite support du vecteur fixe sa direction, tandis que sa longueur est égale à 3.

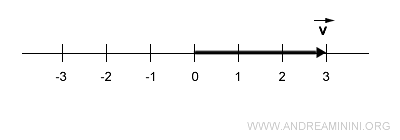
Le vecteur opposé est situé sur la même droite (même direction), de même longueur (3), mais orienté en sens contraire.

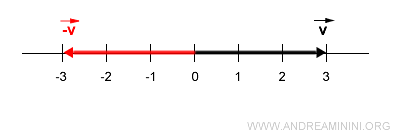
Exemple 2

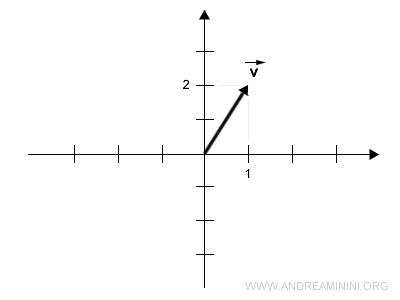
Considérons maintenant un vecteur du plan :

$$ \vec{v} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

Dans un repère cartésien, ce vecteur joint l’origine \( O \) au point de coordonnées \( (1,2) \).

Pour calculer son opposé, il suffit de multiplier \( \vec{v} \) par -1 :

$$ - \vec{v} = -1 \cdot \vec{v} $$

$$ - \vec{v} = -1 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} $$

$$ - \vec{v} = \begin{pmatrix} -1 \cdot 1 \\ -1 \cdot 2 \end{pmatrix} $$

$$ - \vec{v} = \begin{pmatrix} -1 \\ -2 \end{pmatrix} $$

Le vecteur opposé joint donc l’origine au point de coordonnées \( (-1,-2) \).

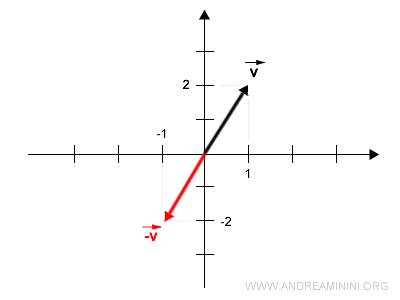
Propriétés et observations

Quelques faits essentiels à propos des vecteurs opposés :

• La somme d’un vecteur et de son opposé est toujours le vecteur nul
  Soit \( \vec{v} \) un vecteur d’un espace vectoriel \( V \). Son opposé \( -\vec{v} \) est l’unique vecteur qui, ajouté à \( \vec{v} \), donne le vecteur nul : $$ \vec{v} + (-\vec{v}) = \vec{0} $$ Cette propriété découle directement de la définition de l’opposé et des axiomes d’addition vectorielle (associativité et commutativité).

  Exemple. Dans \( \mathbb{R}^2 \), soit $$ \vec{v} = \begin{pmatrix} 3 \\ -2 \end{pmatrix} $$ Son opposé est : $$ -\vec{v} = \begin{pmatrix} -3 \\ 2 \end{pmatrix} $$ En additionnant les deux : $$ \vec{v} + (-\vec{v}) = \begin{pmatrix} 3 \\ -2 \end{pmatrix} + \begin{pmatrix} -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 3-3 \\ -2+2 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} $$ On obtient bien le vecteur nul : \( \vec{0} = \begin{pmatrix} 0 \\ 0 \end{pmatrix} \).

Et ainsi de suite.