Représentation vectorielle d’une droite
Un vecteur géométrique définit une direction commune à toutes les droites du plan qui lui sont parallèles.
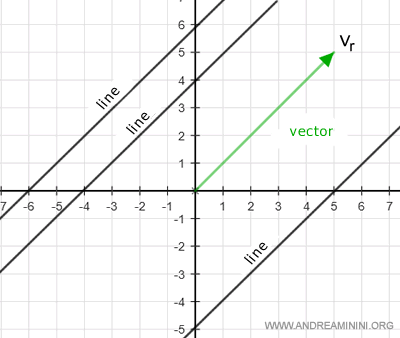
Ainsi, toute droite du plan peut être caractérisée par :
- un vecteur géométrique non nul \( v_r \), appelé vecteur directeur, qui en fixe la direction : $$ v_r = \begin{pmatrix} l \\ m \end{pmatrix} $$
Les valeurs \( l \) et \( m \) sont appelées paramètres directeurs de la droite.
- un point \( P_0 \) du plan appartenant à la droite : $$ P_0 = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$
Exemple
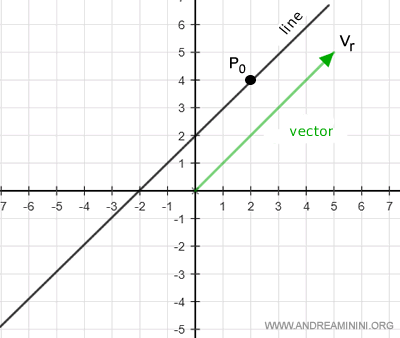
Un point quelconque du plan appartient à la droite s’il existe un scalaire \( \alpha \in \mathbb{R} \) tel que :
$$ OP = OP_0 + \alpha v_r $$
Exemple
Soit le point \( P_1 \) de coordonnées (-5, -3).
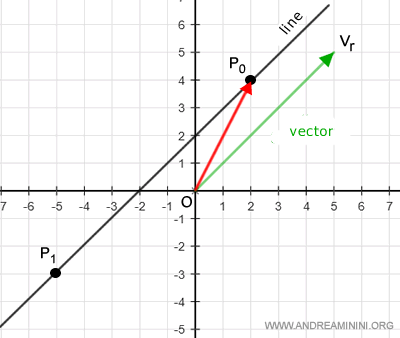
Le point \( P_1 \) appartient à la droite si :
$$ OP_1 = OP_0 + \alpha v_r $$
$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \alpha \begin{pmatrix} 5 \\ 5 \end{pmatrix} $$
En résolvant le système :
$$ \begin{cases} -5 = 2 + 5 \alpha \\ -3 = 4 + 5 \alpha \end{cases} \;\;\Rightarrow\;\; \begin{cases} \alpha = - \tfrac{7}{5} \\ \alpha = - \tfrac{7}{5} \end{cases} $$
Le système est cohérent et donne \( \alpha = -\tfrac{7}{5} \).
Vérification :
$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} + \begin{pmatrix} 5 \cdot ( - \tfrac{7}{5} ) \\ 5 \cdot ( - \tfrac{7}{5} ) \end{pmatrix} $$
$$ \begin{pmatrix} -5 \\ -3 \end{pmatrix} = \begin{pmatrix} 2 - 7 \\ 4 - 7 \end{pmatrix} = \begin{pmatrix} -5 \\ -3 \end{pmatrix} $$
Ainsi, le point \( P_1 \) appartient bien à la droite.
L’ensemble des points de la droite est décrit par l’équation vectorielle : $$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} + \alpha \cdot \begin{pmatrix} l \\ m \end{pmatrix} $$ En la développant, on obtient les équations paramétriques de la droite : $$ \begin{cases} x = x_0 + \alpha l \\ y = y_0 + \alpha m \end{cases} $$
Il existe une infinité de représentations vectorielles et paramétriques, puisque le vecteur directeur peut être multiplié par tout scalaire non nul.
Équations cartésiennes
Le vecteur \( P_0 P_1 \) est parallèle au vecteur directeur \( v_r \).
D’après la théorie, deux vecteurs sont parallèles s’ils sont proportionnels, ce qui revient à écrire :
$$ det \begin{pmatrix} x - x_0 & l \\ y - y_0 & m \end{pmatrix} = 0 $$
En développant le déterminant, on obtient :
$$ m ( x - x_0 ) - l ( y - y_0 ) = 0 $$
C’est l’équation cartésienne de la droite.
Comme pour les équations vectorielles et paramétriques, il existe une infinité d’équations cartésiennes équivalentes.