Opérateur de parité

L’opérateur de parité est l’opérateur mathématique qui décrit la réflexion spatiale, c’est-à-dire la transformation qui inverse les coordonnées spatiales d’un système par rapport à l’origine.

Autrement dit, appliquer la parité revient à remplacer une configuration physique par son image miroir, obtenue en inversant l’orientation de l’espace.

Par exemple, si un point de l’espace possède les coordonnées

$$ x = (x, y, z) $$

alors l’action de l’opérateur de parité $ P $ s’écrit

$$ P(x) = (-x, -y, -z) $$

Cette transformation est appelée inversion spatiale.

Appliquer l’opérateur de parité à un système physique revient donc à l’observer comme s’il était réfléchi par rapport à l’origine, et non par rapport à un plan particulier.

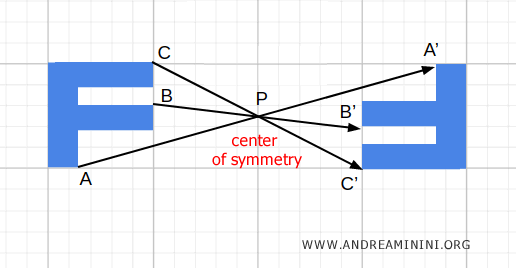
D’un point de vue géométrique, il s’agit d’une symétrie centrale. Cette transformation globale inverse simultanément la gauche et la droite, l’avant et l’arrière, ainsi que le haut et le bas.

À quoi sert la parité ?

L’opérateur de parité joue un rôle central en physique, car certaines interactions fondamentales respectent cette symétrie, tandis que d’autres la violent.

• Si un processus physique reste inchangé sous l’action de la parité, on dit que la parité est conservée.
• Si le processus est modifié, on dit que la parité est violée.

L’étude de la parité constitue ainsi un outil essentiel pour comprendre et classer les systèmes physiques et les particules élémentaires.

Remarque. Dans les interactions électromagnétiques et fortes, la parité est conservée. En revanche, dans les interactions faibles, elle est violée. Dans ce cadre, la nature distingue la gauche de la droite. C’est pourquoi il n’existe que des neutrinos gauchers et des antineutrinos droitiers. La violation de la parité révèle l’une des asymétries les plus profondes de la nature.

Propriétés fondamentales

L’opérateur de parité possède plusieurs propriétés fondamentales.

Lorsqu’il est appliqué deux fois de suite, il ramène le système à sa configuration initiale.

$$ P^2 = I $$

où $ I $ désigne l’opérateur identité.

Exemple. Considérons un point de l’espace de coordonnées : \[ \vec r = (2,-1,3) \] L’opérateur de parité inverse toutes les coordonnées : \[ P(\vec r) = (-2,1,-3) \] Cela correspond à une réflexion du point par rapport à l’origine. Si l’on applique à nouveau l’opérateur de parité, on obtient : \[ P(P(\vec r)) = P(-2,1,-3) = (2,-1,3) \] On retrouve ainsi le point initial, ce qui exprime la relation \( P^2 = I \). \[ P^2(\vec r) = \vec r \]

D’un point de vue physique, effectuer deux inversions spatiales successives revient à n’en effectuer aucune. Le système retrouve donc sa configuration initiale.

Pour cette raison, l’opérateur de parité $ P $ ne peut admettre que deux valeurs propres :

• +1, correspondant à un état de parité paire.
• -1, correspondant à un état de parité impaire.

Vecteurs polaires et vecteurs axiaux

L’opérateur de parité permet également de distinguer les vecteurs polaires des vecteurs axiaux.

• Vecteurs polaires
  Un vecteur polaire, comme la position, la vitesse ou la force, change de signe sous une inversion spatiale : $$ P(\vec{v}) = -\vec{v} $$
• Vecteurs axiaux (pseudovecteur)
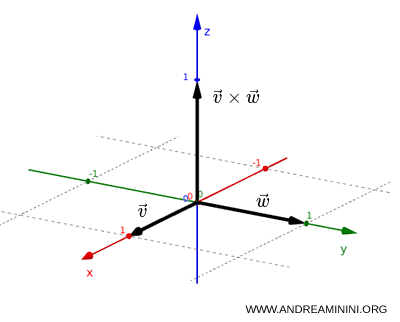
  Un vecteur axial, également appelé pseudovecteur, comme le moment cinétique ou le champ magnétique, ne change pas de signe sous une inversion spatiale : $$ P(\vec v \times \vec w) = (-\vec v) \times (-\vec w) = \vec v \times \vec w = \vec L $$

  Démonstration. Soit \( \vec L = \vec v \times \vec w \), où \( \vec v \) et \( \vec w \) sont des vecteurs polaires. Sous l’action de l’opérateur de parité \( P \), on a $$ P(\vec v) = -\vec v, \quad P(\vec w) = -\vec w $$ et par conséquent $$ P(\vec L) = \vec L $$ Exemple. Considérons deux vecteurs dans le plan : $$ \vec v = (1,0), \qquad \vec w = (0,1) $$ Leur produit vectoriel est un vecteur perpendiculaire au plan, dirigé selon l’axe z : $$ \vec v \times \vec w = (0,0,1) $$ Ce vecteur est un vecteur axial. En appliquant l’inversion spatiale, on obtient : $$ (x,y) \rightarrow (-x,-y) $$ et donc : $$ P(\vec v) = (-1,0), \quad P(\vec w) = (0,-1) $$ En recalculant le produit vectoriel : $$ P(\vec v) \times P(\vec w) = (-1,0) \times (0,-1) = (0,0,1) $$ Le résultat reste inchangé : $$ P(\vec v \times \vec w) = \vec v \times \vec w $$ La direction du vecteur est conservée. Physiquement, l’inversion spatiale inverse les directions, mais pas le sens de rotation.
  

Scalaires et pseudo-scalaires

L’opérateur de parité permet également de distinguer les grandeurs scalaires des pseudo-scalaires.

• Scalaire
  Une grandeur est dite scalaire lorsqu’elle ne change pas de signe sous une inversion spatiale.

  Exemple. La température en un point vaut \( T = 20^\circ \text{C} \). Si l’on applique une inversion spatiale, la température reste inchangée : $$ P(T) = T $$ La température ne possède ni direction ni orientation spatiale. Elle conserve donc la même valeur et le même signe dans la configuration réfléchie. Il s’agit d’une grandeur scalaire.

• Pseudo-scalaire
  Une grandeur est dite pseudo-scalaire si elle change de signe sous une inversion spatiale.

  Exemple. Considérons trois vecteurs : \[ \vec a = (1,0,0) \\ \vec b = (0,1,0) \\ \vec c = (0,0,1) \] Calculons le produit mixte : \[ S = \vec a \cdot (\vec b \times \vec c) \] Comme \( \vec b \times \vec c = (1,0,0) \), on obtient : \[ S = \vec a \cdot (\vec b \times \vec c) = 1 \] Appliquons maintenant la parité : \[ P(\vec a) = (-1,0,0), \quad P(\vec b) = (0,-1,0), \quad P(\vec c) = (0,0,-1) \] Calculons alors : \[ P(S) = P(\vec a) \cdot (P(\vec b) \times P(\vec c)) \] \[ P(S) = (-1,0,0) \cdot \big( (0,-1,0) \times (0,0,-1) \big) \] Comme \( (0,-1,0) \times (0,0,-1) = (1,0,0) \), on obtient : \[ P(S) = (-1,0,0) \cdot (1,0,0) = -1 \] Le résultat final change de signe. Il s’agit donc d’un exemple caractéristique de grandeur pseudo-scalaire.

Valeurs propres de parité des scalaires, pseudoscalaires, vecteurs et pseudovecteurs

L'opérateur de parité \( P \) permet de comprendre comment les grandeurs physiques réagissent lorsque l'on inverse les coordonnées de l'espace. Cette opération simple, mais conceptuellement fondamentale, joue un rôle central dans l'analyse des symétries en physique. À chaque grandeur physique est associée une valeur propre de parité bien définie, qui ne peut prendre que deux valeurs, +1 ou -1.

Les scalaires sont insensibles à l'inversion spatiale. Leur valeur reste inchangée, ce qui explique pourquoi on leur associe la valeur propre +1. Les pseudoscalaires, au contraire, changent de signe sous une transformation de parité et se caractérisent donc par la valeur propre -1.

Grandeur	Transformation de parité	Valeur propre
Scalaire	\( P(s)=s \)	\( +1 \)
Pseudoscalaires	\( P(p)=-p \)	\( -1 \)
Vecteur (ou vecteur polaire)	\( P(\vec v)=-\vec v \)	\( -1 \)
Pseudovecteur (ou vecteur axial)	\( P(\vec a)=\vec a \)	\( +1 \)

La même logique s'applique aux vecteurs ordinaires, aussi appelés vecteurs polaires, comme le déplacement ou la vitesse. Lorsqu'on effectue une transformation de parité, leur orientation spatiale s'inverse. Cette inversion de signe conduit naturellement à leur associer la valeur propre -1.

À l'inverse, les pseudovecteurs, ou vecteurs axiaux, tels que le moment angulaire, présentent un comportement différent. Malgré l'inversion des coordonnées spatiales, ils restent inchangés. Cette invariance justifie l'attribution de la valeur propre +1.

En résumé, les scalaires et les pseudovecteurs sont invariants face à l'inversion spatiale, c'est-à-dire face à une transformation de parité, tandis que les pseudoscalaires et les vecteurs polaires changent de signe. Cette distinction simple constitue un outil essentiel pour analyser les symétries et les lois fondamentales de la physique.

La parité des particules

La parité est un nombre quantique fondamental qui permet de caractériser les particules, au même titre que le spin, la charge électrique, l'isospin, l'étrangeté et d'autres grandeurs clés de la physique des particules. 

Elle décrit la façon dont l'état quantique d'une particule se comporte lorsqu'on effectue une inversion spatiale, autrement dit lorsque toutes les coordonnées de l'espace sont remplacées par leurs opposées.

Cette notion joue un rôle central pour comprendre et distinguer les grandes familles de particules élémentaires.

• Dans le cas des fermions (particules de spin demi-entier), la parité d'une particule est opposée à celle de son antiparticule.
• Pour les bosons (particules de spin entier), en revanche, la particule et son antiparticule possèdent la même parité.

Lorsqu'il s'agit de particules composites, la parité totale s'obtient en multipliant les parités de chacun de leurs constituants. La parité est donc un nombre quantique de nature multiplicative. Cela la distingue d'autres nombres quantiques, comme la charge électrique ou l'étrangeté, qui se combinent de manière additive.

Hadrons

L'interaction forte conservant la parité, les hadrons, c'est-à-dire les baryons et les mésons, sont des états propres de l'opérateur de parité. Ils peuvent ainsi être classés selon la valeur propre associée :

$$ p = \pm 1 $$

Baryons

Par convention, on attribue aux quarks une parité intrinsèque positive :

$$ p(\text{quark}) = +1 $$

Il en découle qu'un baryon constitué de trois quarks possède la parité :

$$ p = (+1)^3 = +1 $$

C'est la raison pour laquelle les baryons, dans leur état fondamental, présentent une parité positive.

Mésons

Les mésons sont formés d'un quark et d'un antiquark. Comme l'antiquark possède une parité intrinsèque opposée à celle du quark, la parité d'un méson dans son état fondamental est égale à -1 :

$$ p = (+1) \cdot (-1) = -1 $$

Dans le cas des mésons excités, une contribution supplémentaire intervient, liée au moment angulaire orbital $ l $. La parité est alors donnée par :

$$ p = (-1)^{l+1} $$

Ici, $ l $ représente le moment angulaire orbital associé au mouvement relatif entre le quark et l'antiquark.

Photon

Le photon est une particule vectorielle de spin 1, associée au potentiel vectoriel électromagnétique. Sa parité intrinsèque est égale à -1 :

$$ p = -1 $$

Pour le photon, la parité intrinsèque n'est pas directement observable comme pour les particules massives. Elle est définie à partir du comportement du champ électromagnétique lorsqu'on effectue une inversion spatiale.

Et ainsi de suite.