Relativité restreinte

La relativité restreinte est une théorie formulée par Albert Einstein en 1905. Elle généralise la mécanique classique aux situations où les objets se déplacent à des vitesses proches de celle de la lumière dans le vide.

En termes simples, la relativité restreinte bouleverse notre perception habituelle de l’espace et du temps, que la mécanique classique considérait comme des grandeurs absolues et indépendantes.

Elle propose un cadre unifié et cohérent de l’espace-temps, dans lequel l’espace et le temps deviennent relatifs et dépendent de l’état de mouvement de l’observateur.

Les deux postulats fondamentaux

La théorie repose sur deux principes vérifiés expérimentalement :

• Principe de relativité
  Les lois de la physique sont les mêmes dans tous les référentiels inertiels, c’est-à-dire ceux qui ne subissent aucune accélération. Aucun référentiel n’est privilégié : les équations de la physique doivent garder la même forme pour tout observateur en mouvement rectiligne uniforme.
• Invariance de la vitesse de la lumière
  La vitesse de la lumière dans le vide est identique pour tous les observateurs, indépendamment du mouvement de la source ou de celui de l’observateur. Elle constitue une constante universelle : $$ c \approx 3 \times 10^8 \,\text{m/s} $$

Ensemble, ces postulats révolutionnent notre manière de comprendre l’espace et le temps, que la mécanique classique considérait comme fixes et absolus.

Ils conduisent notamment à des phénomènes tels que la dilatation du temps, la contraction des longueurs, la relativité de la simultanéité et l’équivalence entre masse et énergie.

Note. En 1915, Einstein a étendu la relativité aux référentiels accélérés et à la gravité, donnant naissance à la Relativité Générale, où l’espace-temps est courbé par la masse-énergie. La relativité restreinte (1905) ne doit donc pas être confondue avec la relativité générale (1915). Ce sont deux théories d’Einstein, mais elles couvrent des domaines différents.

Dilatation du temps

La dilatation du temps est le phénomène par lequel la durée mesurée par un observateur externe est plus longue que celle mesurée dans le système où l’événement a lieu (le référentiel propre).

C’est l’une des conséquences les plus surprenantes de la relativité restreinte : le temps ne s’écoule pas de la même manière pour tous les observateurs.

Une horloge en mouvement retarde par rapport à une horloge au repos.

$$ \Delta t = \gamma \cdot \Delta t_0 \quad \text{avec} \quad \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

Où :

• $\Delta t_0$ est le temps propre, mesuré dans le référentiel où l’horloge est immobile.
  Il est inhérent au phénomène et se mesure dans le cadre de l’événement observé.
• $\Delta t$ est le temps dilaté, observé par un référentiel où l’horloge est en mouvement : pour cet observateur, l’horloge avance plus lentement que celles de son propre système.
• $\gamma$ est le facteur de Lorentz, toujours supérieur à 1 pour $v>0$.

Plus la vitesse relative s’approche de celle de la lumière, plus la dilatation du temps devient marquée : dans le référentiel en mouvement, le temps s’écoule de plus en plus lentement par rapport à celui de l’observateur au repos.

Par exemple, si $t$ représente le temps mesuré sur Terre, alors dans un vaisseau voyageant à une vitesse proche de $c$, le temps $t'$ à bord s’écoule beaucoup plus lentement que sur Terre.

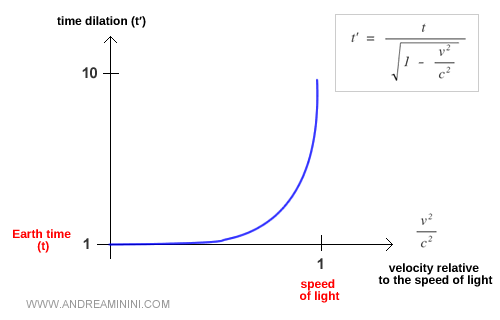
Cet effet est à l’origine du célèbre paradoxe des jumeaux.

Deux jumeaux partent du même référentiel (la Terre). L’un reste sur Terre, tandis que l’autre part dans l’espace à bord d’un vaisseau se déplaçant à une vitesse relativiste, proche de celle de la lumière. À son retour, les deux n’ont plus le même âge :

• Le jumeau resté sur Terre a davantage vieilli.
• Le jumeau voyageur est plus jeune.

L’explication réside dans la dilatation du temps : pendant le voyage, le temps à bord du vaisseau s’est écoulé plus lentement que sur Terre.

La dilatation du temps n’est pas une simple prédiction théorique : elle a été confirmée sans ambiguïté par de nombreuses expériences, notamment en physique des particules à haute énergie.

Exemple : une particule instable (comme un muon) se déplace à vitesse relativiste. Si sa durée de vie moyenne au repos est $ \Delta t_0 = 2.2 \,\mu s $, alors, pour un observateur terrestre la voyant voyager à $v = 0.99 \cdot c$, presque à la vitesse de la lumière, la durée de vie observée sera $ \Delta t = 15.6 \,\mu s $. $$ \gamma \approx \frac{1}{\sqrt{1 - 0.99^2}} \approx 7.1 $$ $$ \Delta t = 7.1 \cdot 2.2 \approx 15.6 \,\mu s $$ Le muon survit donc bien plus longtemps que prévu, car dans son propre référentiel le temps s’écoule plus lentement.

Contraction des longueurs

La contraction des longueurs est le phénomène selon lequel un objet en mouvement paraît plus court dans la direction de son déplacement que dans son état de repos.

Autrement dit, un objet en mouvement est observé plus court dans la direction de son déplacement qu’immobile.

$$ L = \frac{L_0}{\gamma} $$

Où :

• $L_0$ est la longueur propre dans le référentiel où l’objet est immobile.
• $L$ est la longueur contractée, mesurée par un observateur pour qui l’objet est en mouvement.

Exemple : un vaisseau spatial de 100 m au repos voyage à $v = 0.8 \cdot c$ par rapport à la Terre, soit 80 % de la vitesse de la lumière. Dans ce cas, le facteur de Lorentz est 1,667. $$ \gamma = \frac{1}{\sqrt{1 - 0.8^2}} = \frac{1}{\sqrt{0.36}} = \frac{1}{0.6} \approx 1.667 $$ Observé depuis la Terre, le vaisseau mesure environ 60 m. $$ L = \frac{100}{1.667} \approx 60 \,\text{m} $$ Ainsi, il paraît plus court pour l’observateur terrestre.

Relativité de la simultanéité

Deux événements simultanés dans un référentiel peuvent ne pas l’être dans un autre, en mouvement par rapport au premier.

La simultanéité n’est donc pas absolue : elle dépend du référentiel de l’observateur.

Cet effet découle des transformations de Lorentz, qui montrent que l’espace et le temps sont indissociables.

Exemple : un observateur dans un train en mouvement voit deux éclairs frapper simultanément les extrémités d’un wagon. En revanche, un observateur au sol ne les perçoit pas comme simultanés, car la lumière parcourt des distances différentes du fait du mouvement du train.

Équivalence masse-énergie

La masse et l’énergie sont deux manifestations d’une même réalité physique.

Cette équivalence est la célèbre loi d’Einstein :

$$ E = mc^2 $$

Où :

• $E$ est l’énergie contenue dans la masse au repos $m$.
• $c$ est la vitesse de la lumière dans le vide.

Cette relation est à la base de la production d’énergie nucléaire comme des armes atomiques.

Exemple : un gramme de masse (0,001 kg) correspond à : $$ E = 0.001 \cdot (3 \times 10^8)^2 = 9 \times 10^{13} \,\text{J} $$ Une quantité d’énergie colossale, équivalente à l’explosion de plusieurs dizaines de tonnes de TNT.

Et ainsi de suite.