Transformations de Lorentz

Les transformations de Lorentz décrivent la manière dont les coordonnées spatio-temporelles d’un événement se modifient lorsqu’on passe d’un référentiel inertiel à un autre, animé d’une vitesse constante en ligne droite par rapport au premier.

Ces transformations sont au cœur de la relativité restreinte d’Einstein, car elles garantissent que les lois de la physique - et en particulier la vitesse de la lumière dans le vide - restent identiques dans tout référentiel inertiel.

Elles s’appliquent exclusivement aux référentiels inertiels dans le cadre de la théorie de la relativité.

Qu’est-ce qu’un référentiel inertiel ?

Un référentiel inertiel est un système de référence dans lequel la première loi de Newton s’applique : un corps libre, soumis à aucune force extérieure, poursuit indéfiniment son mouvement rectiligne uniforme.

Que dit la relativité restreinte ?

La relativité restreinte énonce que :

aucun référentiel inertiel n’est privilégié par rapport à un autre
les lois de la physique doivent conserver la même forme dans tous les référentiels inertiels, qu’ils soient immobiles ou en mouvement rectiligne uniforme
la vitesse de la lumière dans le vide est une constante universelle, identique pour tous les observateurs

Autrement dit, la lumière n’a pas besoin d’un « milieu » immobile (l’éther) pour se propager, et il n’existe pas de point fixe absolu permettant de mesurer un mouvement universel.

Les équations de transformation de Lorentz
Effets relativistes
Géométrie de l’espace-temps

Les équations de transformation de Lorentz

Considérons deux observateurs (ou référentiels) :

$S$ : le référentiel considéré comme « au repos »
$S'$ : le référentiel se déplaçant à vitesse constante $v$ le long de l’axe $x$

Pour simplifier, limitons-nous à un mouvement le long de l’axe $x$, de sorte que les autres coordonnées spatiales $y$ et $z$ demeurent inchangées.

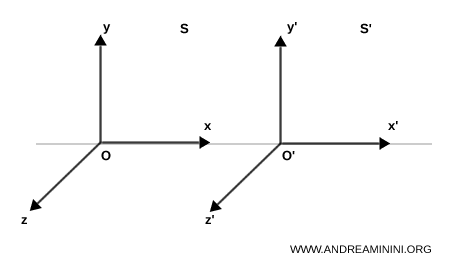
example

Un événement qui se produit dans le référentiel $S$ avec les coordonnées $(x, y, z, t)$ aura, dans le référentiel $S'$, les coordonnées $(x', y', z', t')$ selon les transformations de Lorentz :

$$
\begin{cases}
x' &= \gamma (x - vt) \\
y' &= y \\
z' &= z \\
t' &= \gamma \left(t - \frac{v}{c^2} x\right)
\end{cases}
$$

Le facteur de Lorentz $ \gamma $ est défini par :

$$ \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

On constate que lorsque $v$ est très inférieur à $c$ ( $v \ll c$ ), le facteur $\gamma \approx 1$ et les équations se réduisent alors aux transformations galiléennes classiques.

Que proposait Galilée ? Galilée a introduit les règles classiques du mouvement que nous appelons aujourd’hui les « transformations galiléennes ». Elles ne sont valables que lorsque les vitesses en jeu sont très faibles devant celle de la lumière ($v \ll c$). Selon ces transformations, si un référentiel $S'$ se déplace à vitesse constante $v$ le long de l’axe $x$ par rapport à un référentiel $S$, alors les coordonnées d’un événement se transforment ainsi : $$ \begin{cases} x' &= x - vt \\ y' &= y \\ z' &= z \\ t' &= t \end{cases} $$ Dans cette conception, l’espace varie en fonction du mouvement relatif - la coordonnée $x'$ traduit le déplacement du système - tandis que le temps reste identique pour tous : $t' = t$ est absolu, indépendant du référentiel choisi. En résumé, Galilée considérait que le temps s’écoulait de manière uniforme pour tous les observateurs et que les vitesses s’additionnaient simplement. Cette description fonctionne parfaitement à basse vitesse, mais dès que l’on s’approche de la vitesse de la lumière, ces règles ne suffisent plus et la relativité restreinte devient indispensable.

Effets relativistes

Les transformations de Lorentz ont des conséquences mesurables, confirmées par l’expérience. Voici les principales.

Relativité de la simultanéité
Deux événements qui se produisent au même instant (simultanés) mais en des lieux différents dans le référentiel inertiel $S$ ne sont, en général, plus simultanés dans le référentiel $S'$.
Les événements ne sont simultanés dans $S$ et $S'$ que s’ils se produisent exactement au même point de l’espace. La simultanéité n’est donc pas une notion absolue, mais dépend du référentiel.
Exemple. Deux éclairs frappent en même temps les extrémités d’un train en mouvement pour un observateur immobile au sol (référentiel $S$). Un passager assis au centre du train ne les perçoit pas comme simultanés.

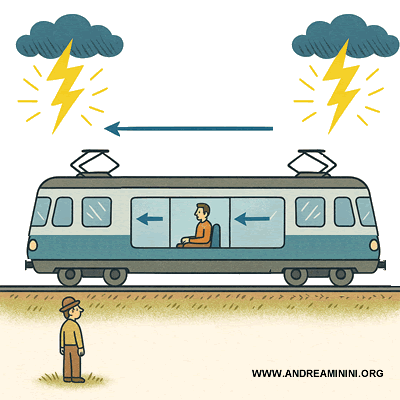
Dans le référentiel du train ($S'$), le passager est en mouvement : la lumière issue de l’avant se rapproche de lui, tandis que celle venant de l’arrière doit le rattraper. Les deux signaux lumineux n’arrivent donc pas en même temps. Ce décalage n’est pas une illusion d’optique, mais la manifestation concrète du fait que la simultanéité définie dans $S$ (observateur au sol) ne coïncide pas avec celle de $S'$ (le passager).

Démonstration
Considérons deux référentiels inertiels, $S$ et $S'$, $S'$ se déplaçant à vitesse constante $v$ le long de l’axe $x$ par rapport à $S$. La transformation de Lorentz pour le temps s’écrit : $$ t' = \gamma \left( t - \frac{v}{c^2}x \right), $$ avec $$ \gamma = \frac{1}{\sqrt{1 - v^2/c^2}}. $$ Supposons que, dans $S$, deux événements $A$ et $B$ aient lieu en des positions différentes $x_A \neq x_B$ mais au même instant : $$ t_A = t_B. $$ Comme ils sont simultanés : $$ t_A - t_B = 0. $$ En appliquant la transformation de Lorentz : $$ t'_A = \gamma \left( t_A - \frac{v}{c^2}x_A \right), \quad t'_B = \gamma \left( t_B - \frac{v}{c^2}x_B \right). $$ En soustrayant : $$ t'_A - t'_B = \gamma \frac{v}{c^2}(x_B - x_A). $$ On voit ainsi que la différence temporelle $t'_A - t'_B$ dans $S'$ est proportionnelle à la distance spatiale $x_B - x_A$ dans $S$. Des événements simultanés dans $S$ mais situés en des lieux distincts cessent de l’être dans $S'$. La simultanéité est préservée dans les deux référentiels uniquement si les événements se produisent au même endroit ($x_A = x_B$).
Contraction des longueurs
Un objet possède une longueur propre $L'$ dans le système $S'$, où il est immobile. Si $S'$ se déplace par rapport à un autre système inertiel $S$, alors, pour un observateur situé dans $S$, la longueur de l’objet apparaît contractée dans la direction du mouvement : $$ L = \frac{L'}{\gamma} $$ Cette contraction ne concerne que la dimension parallèle au déplacement, tandis que toutes les dimensions perpendiculaires restent inchangées.
Exemple. Une tige de 2 mètres, immobile dans $S'$, n’est perçue que comme mesurant 1,2 mètre par un observateur situé dans $S$ lorsque $S'$ se déplace à la vitesse $0,8c$. $$ \gamma = \frac{1}{\sqrt{1 - 0.8^2}} = \frac{1}{0.6} = 1.666... $$ $$
L = \frac{2}{1.666...} \approx 1.2 \text{ mètres} $$ Il en va de même pour un missile filant dans l’espace à une vitesse proche de celle de la lumière : sa longueur se contracte dans la direction du mouvement par un observateur, tandis que ses dimensions transversales demeurent inchangées.

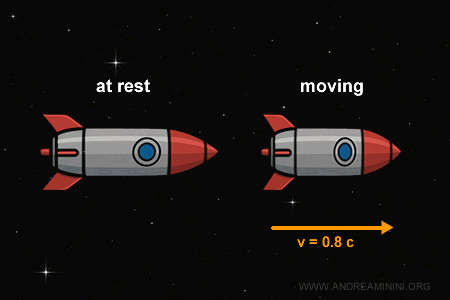
Par exemple, lorsqu'un missile se déplace vers la droite le long de l'axe $x$, son altitude reste inchangée ($y = y'$), mais sa longueur mesurée depuis le référentiel extérieur paraît plus courte ($x' < x$). Ce raccourcissement apparent correspond au phénomène de contraction des longueurs décrit par la relativité restreinte.

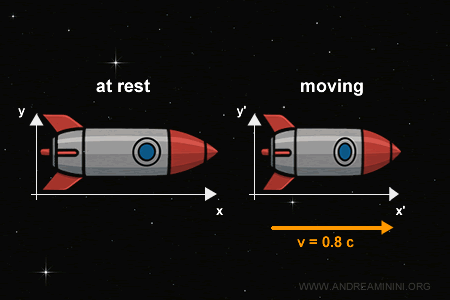
Démonstration de la contraction des longueurs

Considérons une tige rigide de longueur propre $L'$, disposée le long de l’axe $x'$ dans son référentiel de repos $S'$.

Dans ce système, les extrémités ont pour coordonnées :

$$ x'_A = 0, \qquad x'_B = L' $$

La distance entre ces deux points, mesurée à tout instant $t'$, est simplement

$$ L' = x'_B - x'_A $$

Observons maintenant cette même tige depuis un autre référentiel inertiel $S$, dans lequel elle se déplace à la vitesse $v$ le long de l’axe $x$.

Pour évaluer sa longueur dans $S$, il faut relever simultanément les positions de ses deux extrémités au même instant $t$, selon les horloges du système $S$.

Les transformations de Lorentz établissent la relation entre les coordonnées dans les deux référentiels :

$$ x' = \gamma (x - vt), \qquad t' = \gamma \left(t - \frac{v}{c^2}x\right) $$

où le facteur de Lorentz est défini par

$$ \gamma = \frac{1}{\sqrt{1 - v^2/c^2}} $$

Pour l’extrémité $A$, placée en $x'_A = 0$ :

$$ x'_A = 0 = \gamma (x_A - vt) $$

$$ x_A - vt = 0 $$

$$ x_A = vt $$

Pour l’extrémité $B$, située en $x'_B = L'$ :

$$ x'_B = L' = \gamma (x_B - vt) $$

$$ \frac{L'}{\gamma} = x_B - vt $$

$$ x_B = vt + \frac{L'}{\gamma} $$

Comme, dans $S$, les deux extrémités doivent être relevées au même instant $t$, la longueur mesurée s’écrit alors

$$ L = x_B - x_A = \left(vt + \frac{L'}{\gamma}\right) - (vt) = \frac{L'}{\gamma} $$

Ainsi, dans $S$, la tige apparaît plus courte que sa longueur propre $L'$, réduite d’un facteur $\gamma$.

$$ L = \frac{L'}{\gamma} $$

En d’autres termes, un objet en mouvement se présente comme raccourci dans la direction de son déplacement :

$$ L = \frac{L'}{\gamma} $$

Il ressort clairement que cette contraction n’a rien d’une déformation physique de l’objet : c’est une conséquence inévitable de la structure espace-temps décrite par les transformations de Lorentz, qui relient les différents référentiels inertiels.

Remarque. Il faut garder à l’esprit que cette contraction n’affecte que la direction du mouvement. Les dimensions perpendiculaires à la vitesse -telles que $y$ ou $z$, par exemple- restent inchangées, car les transformations de Lorentz ne modifient pas les coordonnées spatiales transversales.
Dilatation du temps
Un intervalle de temps propre $T′$ est la durée mesurée dans le système $S′$, c’est-à-dire là où l’horloge reste immobile, fixée à son support. Si le système $S′$ est en mouvement par rapport à un autre système $S$, alors, pour un observateur situé dans $S$, le temps s’écoule plus lentement dans $S′$ : $$ T = \gamma T' $$
Exemple. Une horloge indique $1$ seconde ($T'=1s$) dans son propre référentiel $ S' $ (un vaisseau spatial) se déplaçant à 90 % de la vitesse de la lumière ($v=0.9c$). Pour un observateur situé dans un référentiel inertiel plus lent $ S $, l’horloge embarquée dans $ S' $ semble battre plus lentement. $$ \gamma = \frac{1}{\sqrt{1-(0.9)^2}} \approx 2.29 $$ $$ T = \gamma T' \approx 2.29 \ s $$ Autrement dit, l’observateur extérieur a l’impression que les aiguilles de l’horloge du vaisseau avancent au ralenti, comme en « slow motion ».

Démonstration de la dilatation temporelle

Considérons une horloge placée dans un système $ S' $, par exemple un vaisseau en mouvement ou même une particule élémentaire.

L’intervalle de temps $ T' $ séparant deux « tic » successifs de l’horloge (par exemple, une seconde) est appelé « temps propre ». Dans ce cadre, les deux événements ne sont rien d’autre que ces deux battements successifs.

$$ T' = t'_B - t'_A $$

Pour un observateur voyageant avec le système $ S' $, l’horloge est fixe sur la paroi. Les deux tics se produisent donc au même endroit (l’origine), séparés par un intervalle temporel de durée $T'$.
- Premier tic : $t'_A=0$ à la position $ x'_A=0$
- Deuxième tic : $t'_B=T'$ à la position $ x'_B=0$
Imaginons maintenant un observateur situé dans un autre système inertiel $S$, par exemple sur Terre, qui voit passer $ S' $ (le vaisseau) à grande vitesse $v$. Comment perçoit-il les battements de l’horloge de $ S' $? Pour répondre, on applique la transformation de Lorentz du temps :

$$ t = \gamma \left(t' + \frac{v}{c^2}x'\right), \qquad \gamma = \frac{1}{\sqrt{1-v^2/c^2}}. $$

Calculons les instants des deux tics tels qu’ils apparaissent depuis le système $S$ :
- Premier tic : $t_A = \gamma (0 + \frac{v}{c^2}\cdot 0) = 0$
- Deuxième tic : $t_B = \gamma (T' + \frac{v}{c^2}\cdot 0) = \gamma T'$
L’intervalle de temps entre ces deux battements, vu dans $S$, est donc :

$$ T = t_B - t_A = \gamma T' $$

Comme $\gamma \geq 1$, il est toujours supérieur ou égal à un, d’où $T \geq T'$. Autrement dit : dans le système $ S $ (celui de la Terre), où l’horloge se déplace avec le vaisseau, l’intervalle entre deux battements est allongé, $T=\gamma T'$.

Cela illustre le principe fondamental : l’écoulement du temps se dilate dès qu’un système est en mouvement.
Addition relativiste des vitesses
En relativité restreinte, les vitesses ne s’additionnent pas de manière linéaire comme en mécanique classique. Si un objet possède une vitesse $u'$ par rapport à un référentiel $S'$, et que ce référentiel se déplace lui-même à la vitesse $v$ par rapport à un autre référentiel $S$, alors la vitesse de l’objet mesurée dans $S$ n’est pas simplement $u = u' + v$. En réalité, elle est donnée par la loi relativiste : $$ u = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$ Le dénominateur garantit que le résultat ne peut jamais excéder $c$, même dans le cas de vitesses extrêmement élevées. Ainsi, si dans $S'$ un objet se déplace déjà à la vitesse de la lumière ($u' = c$), sa vitesse restera toujours $u = c$ dans tout autre référentiel inertiel. Cette formule illustre l’invariance de la vitesse de la lumière et montre clairement que la règle galiléenne $u = u' + v$ n’est valable que pour des vitesses très faibles devant celle de la lumière $ v \ll c$.
Exemple. Une balle se déplaçant à $u' = 0.9c$ dans un train roulant à $v = 0.5c$ n’a pas, par rapport au sol, une vitesse de $1.4c$, mais bien : $$ u = \frac{0.9c + 0.5c}{1 + \frac{0.9 \cdot 0.5}{1}} = \frac{1.4c}{1 + 0.45} = \frac{1.4c}{1.45} \approx 0.9655c $$

Démonstration

En mécanique classique, la composition des vitesses suit la règle galiléenne : si un objet se déplace à la vitesse $ u' $ dans un système $ S' $, et que ce système lui-même se déplace à la vitesse $ v $ par rapport à $ S $, alors la vitesse de l’objet dans $ S $ est tout simplement
$$ u = u' + v $$
Cependant, cette loi est incompatible avec la relativité restreinte, car elle violerait l’invariance de la vitesse de la lumière. Par exemple, si un objet dans $ S' $ se déplaçait à la vitesse $ c $, la somme classique donnerait :
$$ u = c + v > c $$
Ce résultat contredit le postulat d’Einstein, selon lequel la vitesse de la lumière est une constante universelle $ c $, identique dans tous les référentiels inertiels. Les transformations de Lorentz, en revanche, fournissent la formule correcte d’addition des vitesses.

Considérons une particule qui se déplace le long de l’axe $ x $ avec une vitesse $ u' $ dans le référentiel $ S' $. Son déplacement peut s’écrire :
$$ u' = \frac{\Delta x'}{\Delta t'} $$
Du point de vue du système $ S $, les transformations de Lorentz appliquées aux intervalles d’espace et de temps donnent :
$$ \Delta x = \gamma (\Delta x' + v \Delta t'), $$ $$ \Delta t = \gamma \left( \Delta t' + \frac{v}{c^2}\Delta x' \right) $$
La vitesse observée dans $ S $ est alors :
$$ u = \frac{\Delta x}{\Delta t} = \frac{ \gamma (\Delta x' + v \Delta t')}{ \gamma ( \Delta t' + \tfrac{v}{c^2}\Delta x' )} = \frac{\Delta x' + v \Delta t'}{\Delta t' + \tfrac{v}{c^2}\Delta x'} $$
En divisant numérateur et dénominateur par $ \Delta t' $ et en remarquant que $ u'=\Delta x'/\Delta t' $, on obtient :

$$ u = \frac{ \frac{ \Delta x' + v \Delta t' }{ \Delta t' } }{ \frac{ \Delta t' + \tfrac{v}{c^2}\Delta x' }{ \Delta t' } } = \frac{\dfrac{\Delta x'}{\Delta t'}+v}{1+\dfrac{v}{c^2}\dfrac{\Delta x'}{\Delta t'}} = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$

Cette loi relativiste d’addition des vitesses érige la vitesse de la lumière en limite absolue, que nul mouvement ne saurait franchir.

$$ u = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} $$

En effet, si $ u' = c $, alors $ u = c $, quel que soit le valeur de $ v $. De même, lorsque les deux vitesses sont inférieures à $ c $, leur composition demeure toujours en deçà de $ c $.

$$ u = \frac{c + v}{1 + \tfrac{cv}{c^2}} = \frac{c + v}{1 + \tfrac{v}{c}} = \frac{c + v}{1 + \tfrac{v}{c}} \cdot \frac{c}{c} = \frac{c(c + v)}{c + v} = c$$

On en déduit que la vitesse de la lumière constitue une constante universelle, insurpassable par la combinaison de vitesses relatives.

Remarque. Dans la limite classique $ v \ll c $ et $ u' \ll c $, le dénominateur tend vers l’unité $ 1 + \tfrac{u'v}{c^2} \approx 1 $, et la formule relativiste se ramène à la règle galiléenne $ u \simeq u' + v $. $$ u = \frac{u' + v}{1 + \tfrac{u'v}{c^2}} = \frac{u' + v}{1 + 0 } = u'+v $$ Cela démontre que la formule de Lorentz s’accorde parfaitement avec la mécanique classique dans le régime non relativiste.

Géométrie de l’espace-temps

La relativité restreinte ne considère pas l’espace et le temps comme deux réalités distinctes et indépendantes, mais comme les dimensions d’une même structure géométrique que l’on appelle espace-temps.

Chaque événement - c’est-à-dire un fait qui survient en un lieu donné à un instant précis - se décrit par quatre coordonnées : les trois coordonnées spatiales $ (x,y,z) $ et la coordonnée temporelle multipliée par la vitesse de la lumière ( ct ). Ensemble, elles forment un quadrivecteur $(x, y, z, ct)$.

Les transformations de Lorentz préservent une grandeur fondamentale, l’intervalle d’espace-temps :

\[ s^2 = c^2 t^2 - x^2 - y^2 - z^2 \]

Dans l’espace-temps, cet intervalle joue le même rôle que la distance euclidienne dans l’espace ordinaire. De même que la distance reste invariante face aux rotations tridimensionnelles, l’intervalle d’espace-temps demeure inchangé sous les transformations de Lorentz.

En d’autres termes, ces transformations ont définitivement remis en cause la vision classique de l’espace et du temps en abolissant toute notion d’absolu.

Elles constituent le socle mathématique et conceptuel de la relativité restreinte et sont indispensables pour comprendre les phénomènes à très grande vitesse, comme la physique des particules, l’électrodynamique relativiste ou encore la cosmologie.

Et bien plus encore.