Particule Oméga (Ω)
Le baryon Oméga (Ω) appartient à la famille des baryons et est constitué de trois quarks. Dans ce cas particulier, il s’agit exclusivement de quarks étranges ($sss$).
L’existence de cette particule fut prédite en 1961 par le physicien américain Murray Gell-Mann et, indépendamment, par le physicien israélien Yuval Ne'eman.
Sa mise en évidence expérimentale, en 1964 au Laboratoire national de Brookhaven (États-Unis), représenta une étape décisive pour le modèle des quarks de Gell-Mann, en apportant la confirmation directe du décuplet baryonique.
Elle fournit également une preuve irréfutable de l’existence du quark étrange et consacra la validité du schéma de symétrie SU(3) dans la classification des particules.
Propriétés
L’$\Omega^-$ (Oméga moins) se caractérise par les propriétés suivantes :
- Composition en quarks : trois quarks étranges ($sss$)
- Charge électrique : $-1$, chaque quark étrange apportant $-1/3$
- Spin : $3/2$, ce qui le situe dans le décuplet baryonique
- Masse : environ 1672 MeV/c²
- Étrangeté : $S = -3$, ce qui en fait un hyperon exceptionnellement « étrange »
- Découverte : 1964, au synchrotron de Brookhaven, en parfaite concordance avec les prédictions du modèle des quarks et de la symétrie SU(3).
Désintégration
L’$\Omega^-$ est instable et se désintègre exclusivement par interaction faible. Dans ce processus, l’un de ses quarks étranges ($s$) se transforme en quark up ($u$) avec émission d’un boson $W^-$.
Le boson $W^-$ possède une durée de vie extrêmement brève, de l’ordre de $10^{-25}\,\text{s}$. Dans le cas de l’$\Omega^-$, le $W^-$ issu de la transition $s \to u$ ne peut apparaître comme particule réelle, l’énergie disponible étant insuffisante pour produire un $W$ physique (on-shell).
Il se manifeste donc sous forme de boson virtuel, qui se désintègre aussitôt en une paire quark-antiquark plus légère, par exemple : $ W^-_{\text{virt}} \to \bar u + d $
Le système ainsi formé se réorganise : les deux quarks $s$ restants s’associent au nouveau quark $u$ pour former un baryon $\Lambda^0 (uds)$, tandis que le $\bar u$ s’unit à l’un des quarks $s$ pour donner naissance à un méson $K^- (\bar u s)$ :
$$\Omega^- \;\to\; \Lambda^0 + K^-$$
La figure ci-dessous illustre le diagramme de Feynman correspondant :
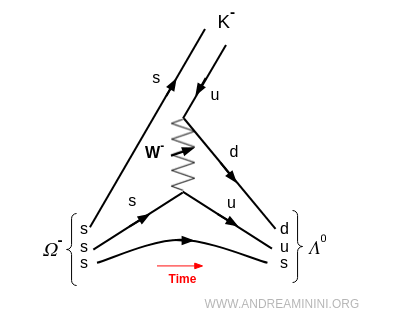
La durée de vie de l’$\Omega^-$ est d’environ $8.2 \times 10^{-11}$ s, plus courte que celle de la $\Lambda^0$, mais néanmoins immensément plus longue que les désintégrations fortes, qui se produisent sur des échelles de temps de l’ordre de $\sim 10^{-23}$ s.
D’autres canaux caractéristiques de la désintégration faible du baryon Oméga incluent :
- $\Omega^- \;\to\; \Xi^0 + \pi^-$
- $\Omega^- \;\to\; \Xi^- + \pi^0$
Ces canaux confirment une fois de plus que l’$\Omega^-$ se désintègre uniquement par interaction faible.