Diagrammes de Young dans la symétrie SU(3)

Les diagrammes de Young sont un outil graphique central pour représenter de manière claire et structurée les représentations du groupe SU(3) et pour comprendre comment ces représentations se combinent par produit tensoriel.

En physique des particules, la symétrie SU(3) décrit la symétrie de saveur associée aux quarks up, down et strange ( u, d, s ).

Grâce à leur dimension visuelle et à leur efficacité conceptuelle, les diagrammes de Young sont largement utilisés pour organiser les mésons, les baryons et, plus généralement, les multiplets de particules en fonction de leurs propriétés de symétrie.

Qu’est-ce qu’un diagramme de Young

Les diagrammes de Young constituent un outil central pour comprendre et organiser les symétries en théorie des groupes et en physique des particules. Ils sont formés de cases disposées en lignes alignées à gauche, selon une règle simple mais essentielle : la longueur des lignes ne doit jamais augmenter lorsqu’on passe de la ligne supérieure aux lignes inférieures.

Dans le cadre du groupe SU(3), la représentation fondamentale est associée au diagramme le plus simple possible, composé d’une seule case. Sa dimension est $ 3 $ et, du point de vue physique, elle correspond au triplet de quarks \(  \{ u,d,s \} \).

On rencontre fréquemment des diagrammes constitués d’une seule case (1), de deux cases sur une même ligne (2), de deux cases empilées en colonne (1,1), ou encore de deux cases sur la ligne supérieure avec une troisième placée juste en dessous (2,1). Ces exemples illustrent différentes manières d’organiser les cases, à condition de respecter strictement les règles de construction.

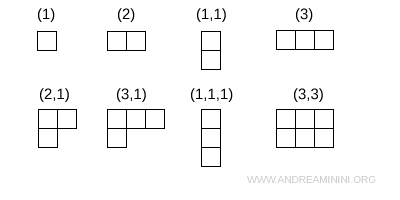
Chaque diagramme de Young encode un type précis de symétrie pour les indices d’une représentation tensorielle. Il fournit ainsi un cadre clair et systématique pour identifier les représentations irréductibles associées.

Règles fondamentales pour SU(3)

Lorsqu’on travaille avec les diagrammes de Young dans le contexte du groupe SU(3), certaines règles fondamentales doivent toujours être respectées.

1. Chaque case représente un indice tensoriel qui se transforme selon la représentation fondamentale \( 3 = \{ u,d,s \} \).
2. Les cases disposées sur une même ligne correspondent à une symétrisation des indices associés.
3. Les cases disposées dans une même colonne correspondent à une antisymétrisation des indices associés.
4. Le diagramme doit être composé de lignes dont la longueur ne croît pas lorsqu’on descend de la première ligne vers les suivantes.
5. Dans SU(3), un diagramme de Young ne peut jamais comporter plus de trois lignes. En effet, l’antisymétrisation complète de quatre indices est identiquement nulle. Cette contrainte joue un rôle clé, car elle limite automatiquement l’ensemble des représentations admissibles du groupe.
6. Produit tensoriel
   Lors d’un produit tensoriel, par exemple $ 6 \otimes 3 $, les cases associées au second facteur sont ajoutées une à une au diagramme de Young du premier facteur. Cette méthode permet de générer progressivement tous les diagrammes compatibles avec les règles de Young. Toute configuration qui viole l’une de ces règles doit être écartée. Si, à une étape donnée, une case ne peut être placée dans aucune position autorisée, on dit que le canal correspondant se ferme.
   • Antisymétrie en colonne
     Dans un produit tensoriel, les cases appartenant à une colonne antisymétrique
     1] ne peuvent pas être toutes placées sur une même ligne
     2] ne peuvent être toutes placées dans une même colonne que si elles prolongent une colonne déjà présente dans le diagramme initial 
   • Vérification finale de la dimension
     La somme des dimensions de toutes les représentations associées aux diagrammes admissibles doit coïncider avec la dimension totale du produit tensoriel. Par exemple, dans $ 6 \otimes 3 $, on compte $ 6 \times 3 = 18 $ états. La somme des représentations obtenues doit donc également être égale à 18, comme dans le cas $ 15 \oplus 3 $.  Si certains canaux se ferment et qu’une partie de la dimension totale n’est pas encore explicitement représentée, la contribution manquante est obtenue par simple soustraction et s’identifie à la représentation compatible.

Pourquoi utiliser les diagrammes de Young ? Les diagrammes de Young permettent de visualiser immédiatement les propriétés de symétrie d'une représentation. Ils offrent un moyen direct d'identifier les représentations autorisées et les combinaisons de quarks admissibles, sans recourir à des calculs algébriques longs et peu intuitifs. L'algèbre abstraite de SU(3) se trouve ainsi traduite en un langage géométrique discret, simple à lire et à interpréter. Les diagrammes de Young ne disent pas quelles particules existent, mais quelles structures de symétrie sont possibles. Le groupe SU(3) fixe le cadre théorique, et les diagrammes de Young en donnent une lecture immédiate.

Combinaisons possibles de multiplets

Pour calculer la dimension des multiplets associés à un diagramme de Young dans la symétrie SU(3), on utilise la formule suivante :

\[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \]

où

• \( N \) désigne la dimension de la représentation fondamentale du groupe. Par exemple, pour SU(2) on a N = 2, pour SU(3) N = 3, pour SU(4) N = 4, et ainsi de suite.
• \( r \) est l'indice de ligne d'une case dans le diagramme de Young, compté de haut en bas à partir de 0.
• \( c \) est l'indice de colonne d'une case dans le diagramme de Young, compté de gauche à droite à partir de 0.
• \( h \) est la longueur du crochet de la case, définie par \[ h = (\text{nombre de cases à droite}) + (\text{nombre de cases en dessous}) + 1 \], le terme \( +1 \) correspondant à la case elle-même.

Le produit est pris sur l'ensemble des cases constituant le diagramme de Young.

Remarque. Le facteur $ (c - r) $ dépend uniquement de la position de la case dans le diagramme, tandis que la longueur du crochet \( h \) dépend exclusivement de la forme du diagramme. Cette formule est valable pour tout diagramme de Young associé au groupe SU(N).

Un exemple concret

Combinaison de deux quarks : \( 3 \otimes 3 \)

Considérons le produit tensoriel de deux représentations fondamentales \( 3 = \{ u,d,s \} \).

$$ 3 \otimes 3 $$

La représentation $ 3 $ est représentée par une seule case portant les indices \(  \{ u,d,s \} \).

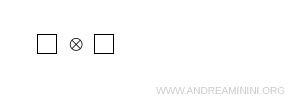
Pour évaluer ce produit tensoriel à l'aide des diagrammes de Young, on ajoute une seconde case à la première dans toutes les positions autorisées par les règles précédentes. Cette construction conduit à deux configurations distinctes.

1. Deux cases sur une même ligne
   Les cases sont placées sur la même ligne, ce qui correspond à une combinaison symétrique. Cette configuration est associée à la représentation \( 6 \).
   
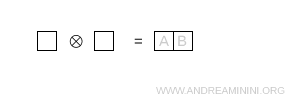   Remarque. La dimension est obtenue en calculant le produit des contributions de chaque case à l'aide de \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \], avec N = 3 pour SU(3).
   

   • Case A. $ r=0 $, $ c=0 $. Une case à droite, aucune en dessous, donc $ h=2 $. $$ \frac{3 + 0 - 0}{2} = \frac{3}{2} $$
   • Case B. $ r=0 $, $ c=1 $. Aucune case à droite ni en dessous, donc $ h=1 $. $$ \frac{3 + 1 - 0}{1} = 4 $$

   Le produit donne $$ dim = \frac{3}{2} \cdot 4 = 6 $$ Cette configuration correspond à une représentation symétrique de dimension $ 6 $.
2. Deux cases en colonne
   Les cases sont disposées verticalement, ce qui correspond à une combinaison antisymétrique. Cette configuration est associée à la représentation \( \bar{3} \).
   
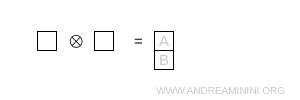   Remarque. En appliquant la même formule avec N = 3 :
   

   • Case A. $ r=0 $, $ c=0 $. Une case en dessous, aucune à droite, donc $ h=2 $. $$ \frac{3 + 0 - 0}{2} = \frac{3}{2} $$
   • Case B. $ r=1 $, $ c=0 $. Aucune case à droite ni en dessous, donc $ h=1 $. $$ \frac{3 + 0 - 1}{1} = 2 $$

   On obtient $$ dim = \frac{3}{2} \cdot 2 = 3 $$ La disposition verticale traduit l'antisymétrie, ce qui correspond à la représentation \( \bar{3} \).

Le résultat final est donc

\[ 3 \otimes 3 = 6 \oplus \bar{3} \]

D'un point de vue physique, cette décomposition signifie que le produit tensoriel de deux triplets de quarks se scinde en six paires de quarks symétriques et trois paires de quarks antisymétriques.

Remarque. Ce résultat correspond parfaitement à l'intuition physique. Une paire de quarks est symétrique si l'échange des deux quarks laisse l'état invariant, et antisymétrique si cet échange introduit un signe global négatif. Pour les trois saveurs de quarks ( \( u,d,s \) ), on obtient six paires symétriques : \[ uu \rightarrow uu \] \[ dd \rightarrow dd \] \[ ss \rightarrow ss \] \[ ud+du \rightarrow ud+du \] \[ us+su \rightarrow us+su \] \[ ds+sd \rightarrow ds+sd \] et trois paires antisymétriques : \[ ud-du \rightarrow - (ud - du) \] \[ us-su \rightarrow - (us - su) \] \[ ds-sd \rightarrow - (ds - sd) \]

Combinaison de trois quarks : \( 3 \otimes 3 \otimes 3 \)

Ce cas joue un rôle central pour comprendre la structure des baryons dans le cadre de la symétrie de saveur SU(3).

$$ 3 \otimes 3 \otimes 3 $$

On part du résultat obtenu pour $ 3 \otimes 3 $, représenté par deux cases disposées horizontalement ou verticalement, puis on ajoute une troisième case. En appliquant de manière systématique les règles des diagrammes de Young, on obtient un ensemble fini de configurations autorisées, chacune correspondant à une représentation bien définie de SU(3).

1. Trois cases sur une même ligne
   Cette configuration est totalement symétrique. Elle conduit à la représentation décuplet \( 10 \).
   
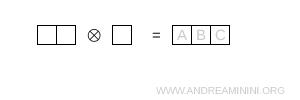   Remarque. La dimension est obtenue en multipliant les contributions associées à chaque case à l'aide de la formule \[ \dim = \prod_{\text{boxes}} \ \frac{N + c - r}{h} \], avec N = 3.
   

   • Case A. $ r=0 $, $ c=0 $. Deux cases à droite, aucune en dessous, donc $ h=3 $. $$ \frac{3 + 0 - 0}{3} = 1 $$
   • Case B. $ r=0 $, $ c=1 $. Une case à droite, aucune en dessous, donc $ h=2 $. $$ \frac{3 + 1 - 0}{2} = 2 $$
   • Case C. $ r=0 $, $ c=2 $. Aucune case à droite ni en dessous, donc $ h=1 $. $$ \frac{3 + 2 - 0}{1} = 5 $$

   Le produit des facteurs donne $$ dim = 1 \cdot 2 \cdot 5 = 10 $$ La disposition horizontale du diagramme traduit une symétrie totale, caractéristique du décuplet.
2. Deux cases sur la première ligne et une sur la seconde
   Cette configuration correspond à une symétrie mixte et conduit à la représentation octet \( 8 \).
   
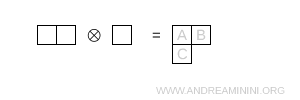   Remarque. La dimension se calcule à nouveau à l'aide de la même formule, avec N = 3.
   

   • Case A. $ r=0 $, $ c=0 $. Une case à droite et une en dessous, donc $ h=3 $. $$ \frac{3 + 0 - 0}{3} = 1 $$
   • Case B. $ r=0 $, $ c=1 $. Aucune case à droite ni en dessous, donc $ h=1 $. $$ \frac{3 + 1 - 0}{1} = 4 $$
   • Case C. $ r=1 $, $ c=0 $. Aucune case à droite ni en dessous, donc $ h=1 $. $$ \frac{3 + 0 - 1}{1} = 2 $$

   On obtient ainsi $$ dim = 1 \cdot 4 \cdot 2 = 8 $$ Ce diagramme décrit donc une représentation octet.
3. Trois cases en colonne
   Cette configuration est totalement antisymétrique et correspond à la représentation singulet \( 1 \).
   
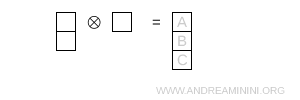   Remarque. En appliquant la formule avec N = 3 :
   

   • Case A. $ r=0 $, $ c=0 $. Deux cases en dessous, aucune à droite, donc $ h=3 $. $$ \frac{3 + 0 - 0}{3} = 1 $$
   • Case B. $ r=1 $, $ c=0 $. Une case en dessous, aucune à droite, donc $ h=2 $. $$ \frac{3 + 0 - 1}{2} = 1 $$
   • Case C. $ r=2 $, $ c=0 $. Aucune case à droite ni en dessous, donc $ h=1 $. $$ \frac{3 + 0 - 2}{1} = 1 $$

   Le produit des facteurs donne $$ dim = 1 \cdot 1 \cdot 1 = 1 $$ Il s'agit d'une représentation unidimensionnelle, identique à sa conjuguée, ce qui justifie la notation $ 1 $.
4. Deux cases sur la première ligne et une sur la seconde
   Cette configuration, bien que visuellement distincte, possède exactement la même forme que le diagramme précédent à symétrie mixte et correspond elle aussi à une représentation octet \( 8 \).
   

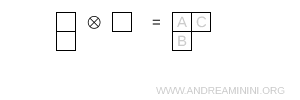
   Remarque. La forme du diagramme étant identique, la représentation associée est la même, à savoir l'octet.

La décomposition finale du produit tensoriel s'écrit donc :

\[ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 \]

Ces multiplets correspondent exactement à ceux observés expérimentalement dans le spectre des baryons.

Remarque. Chaque diagramme de Young possède une interprétation physique directe. Le décuplet (10) décrit des baryons dont la fonction d'onde de saveur est totalement symétrique, comme les états \( \Delta \). Les octets (8) correspondent à des baryons de symétrie de saveur mixte, incluant les nucléons ainsi que les baryons \( \Sigma \) et \( \Xi \). Le singulet (1) représente un état de saveur totalement antisymétrique.

Combinaison de quarks : \( 3 \otimes \bar{3} \)

Dans cet exemple, on s’intéresse au produit tensoriel

$$ 3 \otimes \bar{3} $$

La représentation fondamentale \( 3 \) est figurée par une seule case, tandis que la représentation conjuguée \( \bar{3} \) est représentée par deux cases empilées verticalement. Cette représentation graphique reflète le fait que \( \bar{3} \) peut être interprétée comme une combinaison antisymétrique de deux indices fondamentaux du groupe SU(3).

Le calcul repose sur l’utilisation des diagrammes de Young. La démarche consiste à ajouter la case associée à la représentation \( 3 \) au diagramme de Young correspondant à \( \bar{3} \). En appliquant les règles propres à SU(3), on constate que seules deux configurations distinctes sont autorisées.

• Deux cases sur une ligne et une en dessous
  Ce diagramme de Young est de forme (2,1) et correspond à une représentation de dimension 8.
  

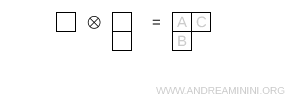
  Note. Cette configuration a déjà été rencontrée dans les exemples précédents. Elle correspond à la représentation octet \( 8 \) de SU(3).

• Trois cases disposées en colonne
  Ce diagramme de Young est de forme (1,1,1) et correspond à une représentation de dimension 1.
  
  
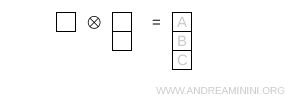
  Note. Cette configuration représente la représentation singulet \( 1 \) de SU(3).

La décomposition du produit tensoriel s’écrit donc :

$$ 3 \otimes \bar{3} = 8 \oplus 1 $$

Les diagrammes de Young offrent ainsi une lecture particulièrement claire de ce résultat. Ils permettent de comprendre immédiatement quels multiplets de saveur apparaissent dans la décomposition et pourquoi aucune autre représentation n’est autorisée dans le cadre de la symétrie SU(3).

Combinaison \( 6 \otimes \bar 3 \)

Intéressons-nous maintenant au calcul du produit tensoriel

$$ 6 \otimes \bar 3 $$

La représentation $ 6 $ est décrite par un diagramme de Young formé de deux cases disposées sur une même ligne, ce qui traduit la symétrisation des indices. La représentation conjuguée $ \bar 3 $ est, au contraire, représentée par deux cases empilées en colonne, mettant en évidence son caractère antisymétrique.

Le calcul s'effectue à l'aide des diagrammes de Young. Dans ce cas précis, une seule configuration non triviale respecte l'ensemble des règles de construction. Elle est donc la seule configuration admissible.

• Trois cases sur la première ligne et une sur la seconde
  Le diagramme de Young obtenu est de type (3,1). Il correspond à une représentation irréductible de dimension $ 15 $.
  
  
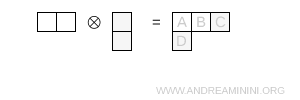
  Note. La dimension est calculée à l'aide de la formule standard de la longueur du crochet \[ \dim = \prod_{\text{cases}} \ \frac{N + c - r}{h} \], en prenant $ N=3 $ tout au long du calcul.
  

  • Case A. L'indice de ligne est $ r=0 $ et l'indice de colonne est $ c=0 $. Deux cases se trouvent à droite et une en dessous. La longueur du crochet vaut donc $ h=2+1+1=4 $ (droite+bas+1).  $$ \frac{N + c - r}{h} = \frac{3 + 0 - 0}{4} = \frac{3}{4} $$
  • Case B. L'indice de ligne est $ r=0 $ et l'indice de colonne est $ c=1 $. Il y a une case à droite et aucune en dessous, d'où $ h=1+0+1=2 $ (droite+bas+1).  $$ \frac{N + c - r}{h} = \frac{3 + 1 - 0}{2} = 2 $$
  • Case C. L'indice de ligne est $ r=0 $ et l'indice de colonne est $ c=2 $. Aucune case ne se trouve ni à droite ni en dessous, ce qui donne $ h=0+0+1=1 $ (droite+bas+1).  $$ \frac{N + c - r}{h} = \frac{3 + 2 - 0}{1} = 5 $$
  • Case D. L'indice de ligne est $ r=1 $ et l'indice de colonne est $ c=0 $. Il n'y a ni case à droite ni case en dessous. On obtient donc $ h=0+0+1=1 $ (droite+bas+1).  $$ \frac{N + c - r}{h} = \frac{3 + 0 - 1}{1} = 2 $$

  En multipliant l'ensemble des facteurs, on obtient la dimension totale $$ \dim = \frac{3}{4} \cdot 2 \cdot 5 \cdot 2 = 15 $$ Cette représentation est dite à symétrie mixte.
• Aucune autre configuration admissible
  Les deux cases associées à la colonne antisymétrique ne peuvent pas être placées simultanément sur une même ligne, car cela imposerait une symétrisation incompatible avec l'antisymétrie. Elles ne peuvent pas non plus être placées toutes les deux dans une même colonne, puisque le diagramme initial ne comporte aucune colonne pouvant être prolongée. Si l'on ajoute une seule case sur la ligne inférieure, la seconde case ne peut être placée nulle part et le canal de composition correspondant se ferme.
  
  
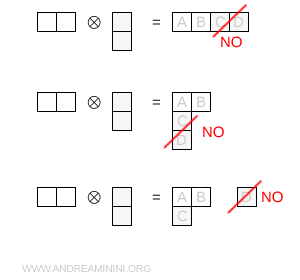
  Solution. Dans ce cas, la représentation compatible restante est déterminée par un simple raisonnement sur les dimensions. La dimension totale du produit tensoriel \( 6 \otimes \bar 3 \) est \( 6 \times 3 = 18 \). Comme une représentation de dimension 15 a déjà été identifiée, il reste $$ 18 - 15 = 3 $$ La représentation manquante dans la décomposition est donc \( 3 \), qui est bien une représentation irréductible admissible de SU(3).

La décomposition finale du produit tensoriel s'écrit ainsi

$$ 6 \otimes \bar 3 = 15 \oplus 3 $$

Ce résultat illustre clairement l'efficacité des diagrammes de Young. Ils offrent un cadre visuel et systématique pour analyser la structure des représentations de SU(3) et comprendre pourquoi certains multiplets apparaissent naturellement, tandis que d'autres sont exclus par les règles de symétrie.

Et ainsi de suite.