Symétries discrètes en physique des particules : C, P et T

En physique des particules, les symétries C, P et T sont des symétries discrètes qui décrivent comment les lois fondamentales de la nature se comportent lorsqu'on leur applique certaines transformations idéalisées.

Contrairement aux transformations continues, comme les rotations ou les translations, il s'agit d'opérations bien définies qui modifient en profondeur la description du système physique étudié.

Les principales symétries discrètes analysées en physique des particules sont :

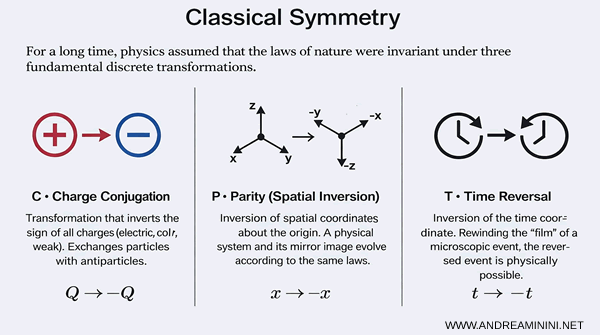
• Symétrie C (conjugaison de charge)
  Elle remplace chaque particule par son antiparticule correspondante, en inversant le signe de toutes les charges. Elle permet d'étudier le comportement des lois physiques lorsque la matière est échangée avec l'antimatière.
• Symétrie P (parité)
  Elle correspond à une inversion spatiale des coordonnées, comparable à une réflexion dans un miroir qui échange la gauche et la droite. Elle sert à vérifier si un processus physique reste invariant sous une inversion de l'espace.
• Symétrie T (inversion du temps)
  Elle consiste à inverser le sens du temps et à analyser un processus comme s'il se déroulait à rebours. Elle permet d'examiner si les lois de la physique décrivent de la même manière l'évolution vers le passé et vers le futur.

 

Pendant longtemps, ces symétries ont été considérées comme universellement valides. Cette idée s'inscrivait dans une vision classique d'une nature fondamentalement symétrique.

À partir des années 1950, plusieurs expériences ont toutefois montré que certaines de ces symétries sont violées, en particulier dans le cadre de l'interaction faible. Cette découverte a profondément modifié notre compréhension des lois fondamentales et constitue encore aujourd'hui un axe majeur de recherche en physique des particules.

Les violations des symétries C, P et CP révèlent que la nature n'est pas parfaitement symétrique, tandis que la conservation de CPT demeure l'un des principes les plus solides et les mieux établis de la physique théorique moderne.

Dans ce cadre, l'étude des symétries discrètes joue un rôle central, à la fois comme socle conceptuel du Modèle standard et comme outil pour explorer des théories au-delà de celui-ci.

Symétrie C (conjugaison de charge)

La symétrie C, ou conjugaison de charge, consiste à remplacer chaque particule par son antiparticule correspondante.

Cette transformation agit directement sur l'identité des particules élémentaires, en inversant l'ensemble des nombres quantiques additifs associés aux charges.

Ainsi, une particule de charge négative, comme l'électron, est transformée en une particule de même masse et de même spin, mais de charge opposée, le positron.

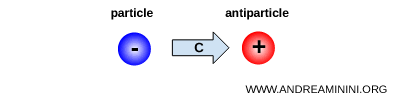
D'un point de vue physique, la transformation C inverse le signe de toutes les charges, non seulement la charge électrique, mais aussi celles associées aux autres interactions fondamentales, comme la charge faible et la charge de couleur.

Par exemple, un quark up de charge électrique \( +\tfrac{2}{3} \) et d'une couleur donnée est transformé, sous l'action de la symétrie C, en un antiquark up de charge électrique \( -\tfrac{2}{3} \) et de l'anticouleur correspondante. De la même manière, un neutrino est transformé en son antineutrino, avec des nombres quantiques faibles de signe opposé.

Quelles interactions fondamentales conservent la symétrie C ?

Les interactions électromagnétique, forte et gravitationnelle respectent la symétrie C.

Autrement dit, remplacer systématiquement toutes les particules par leurs antiparticules correspondantes ne modifie pas la forme mathématique des équations qui décrivent ces interactions.

L'interaction faible, en revanche, viole la symétrie C de manière maximale.

Un exemple particulièrement parlant est fourni par les neutrinos. Un neutrino gaucher, après application de la transformation C, devient un antineutrino gaucher. Or, dans le Modèle standard, les antineutrinos gauchers ne participent pas aux interactions faibles. Ce fait met en évidence, de manière directe, la non-conservation de la symétrie C.

Cette violation joue également un rôle important en cosmologie car, combinée à la violation de CP, elle contribue à expliquer l'asymétrie observée entre la matière et l'antimatière dans l'Univers.

Symétrie P (parité)

La transformation de parité (P) inverse le signe des coordonnées spatiales. En trois dimensions, elle correspond à une inversion centrale par rapport à l'origine.

\[ (x,y,z) \rightarrow (-x,-y,-z) \]

Autrement dit, chaque axe cartésien voit son orientation inversée.

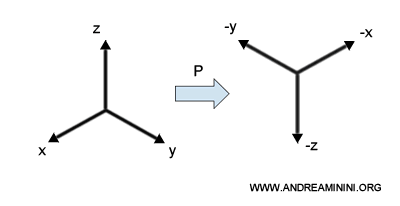
D'un point de vue physique, la parité revient à observer un phénomène à travers un miroir idéal qui inverse toutes les directions de l'espace.

Lorsque la symétrie P est conservée, le processus physique et son image spéculaire obéissent aux mêmes lois et sont physiquement indiscernables.

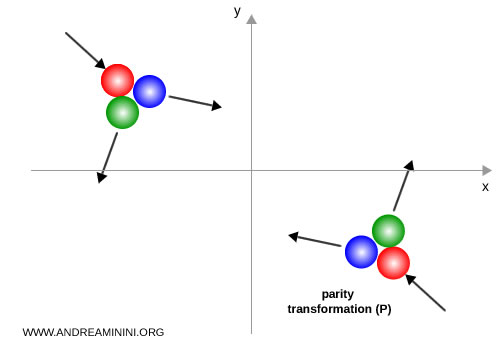
Par exemple, lors d'une collision classique entre des billes de billard, la dynamique du processus reste inchangée même après inversion de toutes les coordonnées spatiales. La mécanique classique est en effet invariante sous la transformation de parité.

La plupart des interactions fondamentales conservent la symétrie de parité P, notamment les interactions forte, électromagnétique et gravitationnelle.

Dans ces cas, les processus physiques se déroulent donc de la même manière lorsque la gauche et la droite sont interverties.

Toutes les interactions ne possèdent toutefois pas cette propriété. L'interaction faible viole la symétrie de parité P. Cette violation montre que la nature distingue de manière intrinsèque les configurations gauches et droites, introduisant une asymétrie fondamentale dans les lois physiques.

En 1957, l'expérience menée par Chien Shiung Wu sur la désintégration bêta du cobalt 60 a fourni une preuve expérimentale décisive de la violation de la symétrie de parité par l'interaction faible.

Les noyaux de cobalt 60, refroidis et alignés à l'aide d'un champ magnétique, émettaient des électrons de manière préférentielle dans une direction opposée au spin nucléaire, rompant ainsi la symétrie miroir.

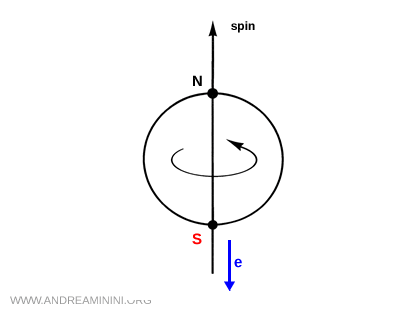
Étant donné que le spin est un pseudovecteur et ne change pas de signe sous une inversion spatiale, on s'attendrait, après application de la transformation de parité P, à une émission des électrons dans la même direction que le spin. Ce comportement n'est pas observé dans la nature, ce qui constitue une preuve expérimentale claire de la violation de la symétrie de parité.

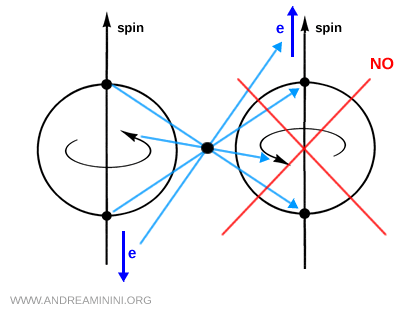
La conclusion est sans ambiguïté : à l'échelle fondamentale, la nature distingue la gauche de la droite.

L'interaction faible est chirale. Seules les composantes gauches des particules et les composantes droites des antiparticules participent aux interactions faibles chargées.

Remarque. En mécanique quantique, les états peuvent être classés selon leur comportement sous la transformation de parité. Un état est dit pair si sa fonction d'onde reste inchangée, et impair si elle change de signe. Cette distinction est particulièrement utile pour l'étude des états liés et des processus de désintégration.

Symétrie T (inversion temporelle)

La symétrie T décrit l'invariance des lois physiques lorsqu'on inverse le sens du temps. De manière intuitive, une transformation T correspond à un renversement de la flèche du temps.

\[ t \rightarrow -t \]

Lorsqu'une théorie est invariante sous T, un processus physique observé « à l'envers » obéit aux mêmes lois dynamiques que celles qui gouvernent son évolution vers l'avant.

Un exemple simple et parlant est celui des collisions entre billes de billard. Une bille rouge percute simultanément deux autres billes, l'une bleue et l'autre verte, qui s'éloignent ensuite dans des directions différentes. Si l'on observe la scène en sens inverse, les deux billes convergent vers la bille rouge, entrent en collision avec elle et la font repartir en arrière. Du point de vue des lois de la mécanique classique, les deux descriptions sont parfaitement admissibles, sans distinction fondamentale entre passé et futur.

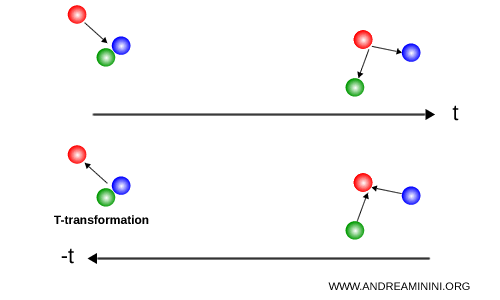
À l'échelle macroscopique, cette symétrie semble toutefois brisée par la deuxième loi de la thermodynamique, qui introduit une direction privilégiée du temps associée à l'augmentation irréversible de l'entropie.

Cette asymétrie temporelle n'est cependant pas considérée comme fondamentale. Elle est interprétée comme un phénomène émergent d'origine statistique, lié au comportement collectif de systèmes comportant un très grand nombre de degrés de liberté.

À l'échelle microscopique, en revanche, la plupart des lois dynamiques fondamentales restent invariantes sous l'inversion temporelle.

Il existe néanmoins une exception de tout premier plan. Étant donné que le théorème CPT doit être satisfait de manière exacte, l'observation expérimentale d'une violation de la symétrie CP implique nécessairement l'existence d'une violation de la symétrie T dans les interactions faibles. Bien que cette violation soit fondamentale, sa mise en évidence directe demeure particulièrement difficile sur le plan expérimental.

Symétrie CP

La symétrie CP est définie comme l'application successive de la conjugaison de charge (C) et de la parité (P).

Lors d'une transformation CP, une particule est d'abord remplacée par son antiparticule par l'opération C, puis les coordonnées spatiales de l'état obtenu sont inversées par l'opération de parité P.

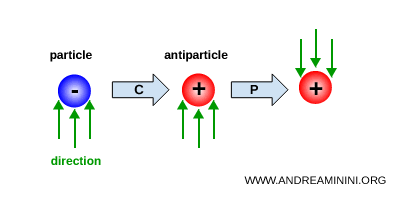
Après la découverte de la violation de la parité, on a d'abord envisagé que la symétrie CP puisse être conservée et représenter une symétrie plus profonde des lois de la nature.

En effet, lorsque les transformations C et P sont appliquées conjointement au cas des neutrinos, on obtient un antineutrino droitier, en accord avec les observations expérimentales.

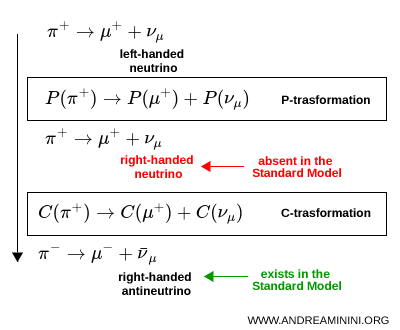
Cette hypothèse a toutefois été réfutée en 1964, lorsque l'étude des désintégrations des kaons neutres a mis en évidence une violation de la symétrie CP dans les interactions faibles.

On a notamment observé que les kaons et les antikaons ne se comportent pas de façon strictement identique, même après application de la transformation CP.

Remarque. Cette découverte a eu des conséquences majeures en physique théorique. La violation de CP constitue en effet l'une des conditions nécessaires pour expliquer l'asymétrie observée entre matière et antimatière dans l'Univers. En son absence, matière et antimatière auraient été produites en quantités égales au cours des premiers instants de l'évolution cosmique et se seraient ensuite annihilées mutuellement.

Symétrie CPT et théorème CPT

La symétrie CPT résulte de la combinaison des trois transformations discrètes précédentes : la conjugaison de charge, la parité et l'inversion temporelle.

Le théorème CPT énonce que toute théorie quantique des champs locale, invariante sous les transformations de Lorentz et gouvernée par un Hamiltonien hermitien, doit être invariante sous la transformation CPT combinée.

Autrement dit, l'inversion simultanée de la charge, de l'espace et du temps laisse inchangées les lois fondamentales de la physique. Même lorsque les symétries C, P ou CP sont violées individuellement, la symétrie CPT demeure une invariance exacte.

Par exemple, si $ \Psi $ désigne un état physique, alors $ \Psi_{CPT} $ est également un état physique et obéit aux mêmes lois fondamentales.

$$ \Psi \ \text{(État physique)} \xrightarrow{C} C(\Psi) \xrightarrow{P} PC(\Psi) \xrightarrow{T} \Psi_{CPT} $$

Il en résulte qu'un univers constitué d'antimatière, souvent qualifié d'univers miroir, réfléchi spatialement et évoluant à rebours dans le temps, serait régi par exactement les mêmes lois physiques que notre propre univers.

Le théorème CPT implique également l'existence d'une violation de la symétrie T.

Pour préserver l'invariance CPT, toute violation de la symétrie CP doit nécessairement s'accompagner d'une violation correspondante de la symétrie T, c'est-à-dire de l'invariance sous inversion temporelle.

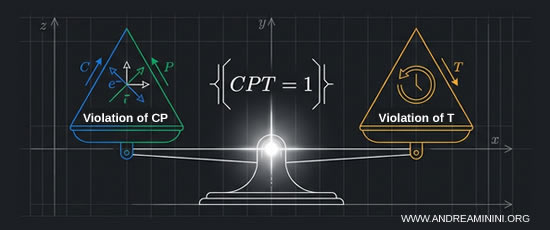
Les lois microscopiques de la physique ne sont donc pas parfaitement symétriques vis-à-vis du temps.

Remarque. Puisqu'il est établi expérimentalement que les symétries C et P sont violées, le théorème CPT impose l'existence d'une violation de la symétrie T afin que la transformation CPT combinée reste une symétrie exacte des lois fondamentales. Ainsi, toute violation de la symétrie CP entraîne nécessairement une violation de la symétrie T. Il est important de souligner que cette forme d'irréversibilité temporelle est conceptuellement distincte de la flèche thermodynamique du temps, dont l'origine est statistique et macroscopique.

À ce jour, la symétrie CPT est la seule combinaison de ces transformations dont la conservation stricte a été confirmée par l'ensemble des observations expérimentales. Aucune indication expérimentale d'une violation de la symétrie CPT n'a été mise en évidence.

Toute violation éventuelle de la symétrie CPT impliquerait une rupture de l'invariance de Lorentz et conduirait à une remise en question profonde de nos théories physiques fondamentales.

Et ainsi de suite.