Particules Sigma

Les particules Sigma, notées par la lettre grecque $ \Sigma $, sont des baryons constitués de trois quarks. Elles appartiennent à la famille des particules soumises à l’interaction forte et se distinguent par la présence d’un quark étrange (s), à l’origine du nombre quantique appelé étrangeté.

Chaque particule Sigma est formée de trois quarks selon les combinaisons suivantes :

$ \Sigma^+ = uus $
$ \Sigma^0 = uds $
$ \Sigma^- = dds $

Dans tous les cas, un quark étrange est présent, accompagné de deux quarks de type up (u) et down (d).

Charge électrique

La charge électrique d’une particule correspond à la somme algébrique des charges de ses quarks constitutifs. On utilise les valeurs suivantes :

$ q(u) = +\frac{2}{3} $
$ q(d) = -\frac{1}{3} $
$ q(s) = -\frac{1}{3} $

On obtient ainsi les charges électriques des particules Sigma :

$ q(\Sigma^+) = +1 $
$ q(\Sigma^0) = 0 $
$ q(\Sigma^-) = -1 $

Par exemple, la particule $ \Sigma^+ $ est composée de deux quarks up et d’un quark étrange (uus). Sa charge électrique est : $$ q(\Sigma^+) = q(u) + q(u) + q(s) = \frac{2}{3} + \frac{2}{3} - \frac{1}{3} = \frac{3}{3} = +1 $$ La particule $ \Sigma^0 $ est formée d’un quark up, d’un quark down et d’un quark étrange (uds). Sa charge est : $$ q(\Sigma^0) = q(u) + q(d) + q(s) = \frac{2}{3} - \frac{1}{3} - \frac{1}{3} = 0 $$ Enfin, la particule $ \Sigma^- $ contient deux quarks down et un quark étrange (dds), ce qui donne : $$ q(\Sigma^-) = q(d) + q(d) + q(s) = -\frac{1}{3} - \frac{1}{3} - \frac{1}{3} = -1 $$

Isospin des particules Sigma

Les particules Sigma possèdent un isospin total égal à 1.

Cela s’explique par le fait que l’isospin concerne uniquement les quarks up et down, tandis que le quark étrange n’y participe pas.

Les quarks u et d peuvent se combiner de manière symétrique, ce qui conduit à un isospin total :

$$ I = 1 $$

Explication. Les quarks $ u $ et $ d $ forment un doublet d’isospin, tandis que le quark étrange est un singulet vis-à-vis de cette symétrie. Chacun des quarks u et d possède un isospin $ \tfrac12 $, avec pour troisième composante : $$ I_3(u) = +\frac{1}{2} $$ $$ I_3(d) = -\frac{1}{2} $$ La structure du groupe SU(2) implique que la combinaison de deux états d’isospin $ \tfrac12 $ ne peut conduire qu’à deux valeurs possibles du total : \[ \frac{1}{2} \otimes \frac{1}{2} = 1 \oplus 0 \] On obtient ainsi un état symétrique d’isospin $ I = 1 $ et un état antisymétrique d’isospin $ I = 0 $.

L’état symétrique d’isospin $ I = 1 $ forme un triplet associé aux particules Sigma : \[ \begin{aligned} |1,+1\rangle &= uu \\ |1,0\rangle &= \frac{1}{\sqrt{2}}(ud + du) \\ |1,-1\rangle &= dd \end{aligned} \] L’état antisymétrique d’isospin $ I = 0 $ correspond à la particule Lambda : \[ |0,0\rangle = \frac{1}{\sqrt{2}}(ud - du) \]

Il est important de souligner que les particules Sigma et Lambda possèdent exactement la même composition en quarks (uds), mais diffèrent par la manière dont ces quarks s’organisent dans l’espace de l’isospin.

Pourquoi attribue-t-on I = 1 aux particules Sigma (Σ) et I = 0 à la Lambda (Λ) ?

Les observations expérimentales montrent que les particules Sigma existent sous trois états de charge distincts ($ \Sigma^+, \Sigma^0, \Sigma^- $). Or, le nombre d’états d’un multiplet d’isospin est donné par la relation :

$$ 2I + 1 = 3 \Rightarrow I = 1 $$

Les Sigma forment donc un triplet. Cela signifie que la partie isospin de leur fonction d’onde est symétrique, c’est-à-dire inchangée lorsqu’on échange les quarks u et d :

$$ uu $$ $$ dd $$ $$ \frac{1}{\sqrt{2}}(ud + du) $$

La particule Lambda, en revanche, ne possède qu’un seul état observable ($ \Lambda^0 $), ce qui implique :

$$ 2I + 1 = 1 \Rightarrow I = 0 $$

Elle correspond donc à un singulet, dont la fonction d’onde d’isospin est antisymétrique et change de signe lors de l’échange des quarks u et d :

$$ \frac{1}{\sqrt{2}}(ud - du) $$

En résumé, la différence entre les particules Sigma et Lambda ne tient pas à leur composition en quarks, mais à la structure de leur état d’isospin.

Lorsque l’isospin total vaut $ I = 1 $, le nombre d’états possibles est :

\[ 2I + 1 = 2 \cdot 1 + 1 = 3 \]

Ces états correspondent aux valeurs suivantes de la troisième composante de l’isospin :

$$ I_3 = \{ +1,\ 0,\ -1 \} $$

Dans le cas des particules Sigma, cela correspond à :

$ \Sigma^+ $
$ \Sigma^0 $
$ \Sigma^- $

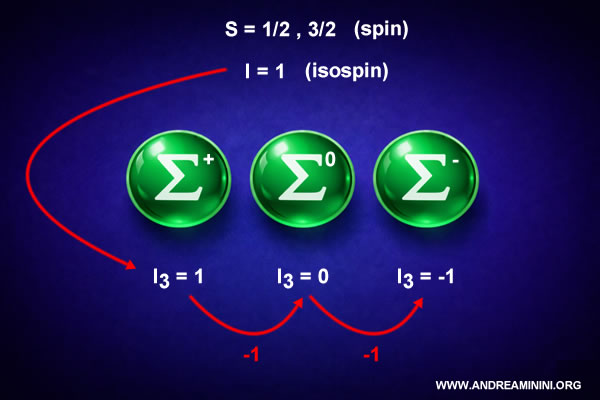
sigma isospin

Spin des particules Sigma

Il existe deux familles distinctes de particules Sigma, qui se distinguent par la valeur de leur spin total.

Sigma (Σ)
Les particules Sigma ordinaires possèdent un spin $ \frac{1}{2} $ et appartiennent à l’octet baryonique. Les spins des quarks ne sont alors pas tous alignés, par exemple dans une configuration du type ↑↑↓, ce qui conduit à un spin total de $ \tfrac{1}{2} $ : $$ \tfrac{1}{2} + \tfrac{1}{2} - \tfrac{1}{2} = \tfrac{1}{2} $$
Sigma étoile (Σ*)
Les particules Sigma* possèdent un spin $ \frac{3}{2} $ et appartiennent au décuplet baryonique. Dans ce cas, les trois spins des quarks sont alignés (↑↑↑), ce qui conduit à un spin total de $ \tfrac{3}{2} $ : $$ \tfrac{1}{2} + \tfrac{1}{2} + \tfrac{1}{2} = \tfrac{3}{2} $$ Ces états correspondent à des baryons excités, caractérisés par un alignement complet des spins.

La différence entre ces deux familles provient donc de l’orientation relative des spins des quarks.

Cela explique pourquoi des particules ayant la même composition en quarks peuvent présenter des masses différentes et des valeurs de spin distinctes.

Et ainsi de suite.