Antiparticules
Chaque particule élémentaire possède une antiparticule associée, de même masse et de même spin, mais portant des charges additives opposées (électrique, baryonique, leptonique, etc.).
Une antiparticule n’est pas simplement l’image en miroir d’une particule : c’est une entité distincte, dotée d’un rôle physique bien précis dans les interactions.
Voici quelques exemples :
| Particule | Antiparticule |
|---|---|
| Électron $e^-$ | Positron $e^+$ |
| Proton $p $ | Antiproton $\overline{p} $ |
| Neutron $n $ | Antineutron $\overline{n} $ |
| Quark $u $ | Antiquark $\overline{u} $ |
Par exemple, l’antiparticule de l’électron (de charge négative) est le positron, qui possède la même masse et le même spin, mais une charge positive.
De la même façon, le proton (charge positive) a pour antiparticule l’antiproton, porteur d’une charge négative, et ainsi de suite.
Remarque. Par convention, les antiparticules sont généralement notées par une barre placée au-dessus du symbole de la particule. Ainsi, l’antiparticule du proton $p$ se note $ \overline{p} $. Mais il existe des exceptions : le positron (ou antielectron) s’écrit presque toujours $ e^+ $ au lieu de $ \overline{e} $, et l’antimuon $ \mu^+ $ plutôt que $ \overline{\mu} $.
Il convient de préciser que l’« opposition » des charges ne se limite pas au seul cas de la charge électrique. Une antiparticule peut aussi se distinguer par d’autres nombres quantiques additifs, comme le nombre baryonique, le nombre leptonique ou encore d’autres nombres quantiques.
Par exemple, le neutron n’ayant pas de charge électrique, son antiparticule - l’antineutron - ne se différencie pas par la charge mais par d’autres nombres quantiques.
Certaines particules sont identiques à leur propre antiparticule. On les appelle des particules autoconjuguées.
Une particule est dite autoconjuguée lorsqu’il est impossible de la distinguer de son antiparticule, autrement dit lorsque sa charge électrique et toutes ses autres charges additives sont nulles.
Exemples de particules autoconjuguées :
| Particule | Autoconjuguée ? | Remarques |
|---|---|---|
| Photon $ \gamma $ | Oui | Sans charge |
| Boson $Z^0 $ | Oui | Neutre |
| Méson $\pi^0 $ | Oui | Pion neutre |
| Gluons | Oui / Non | Selon la configuration |
Dans le cas des neutrinos, on ignore encore s’ils sont des neutrinos de Dirac (avec antiparticules distinctes) ou des neutrinos de Majorana (autoconjugués). Cette question demeure ouverte en physique des particules.
Différence entre antiparticules et antimatière
La matière constituée exclusivement d’antiparticules est appelée antimatière.
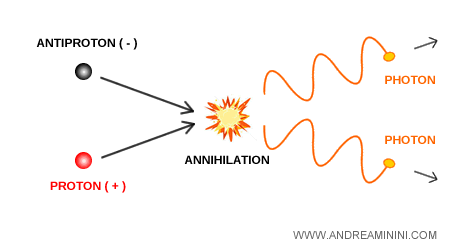
L’antimatière possède une propriété remarquable : lorsqu’elle rencontre la matière, les deux s’annihilent en libérant de l’énergie sous forme de photons gamma.
$$ e^- + e^+ \rightarrow \gamma + \gamma $$
Cependant, la simple existence d’un positron isolé ne suffit pas à constituer de l’antimatière. Il faut pour cela un système organisé, comme un antiatome ou une molécule stable d’antimatière.
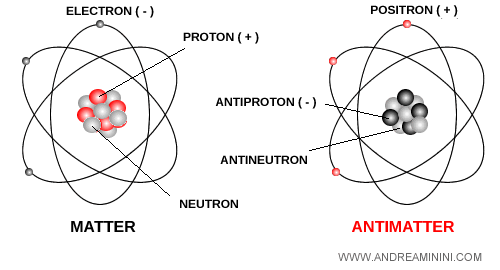
En d’autres termes, l’antimatière se compose d’antiparticules assemblées, mais toute antiparticule isolée ne constitue pas de l’antimatière.
Exemple. Un atome d’antihydrogène est formé d’un antiproton $ \overline{p} $ au sein du noyau et d’un positron $ e^+ $ (l’équivalent d’antimatière de l’électron) en orbite autour. Contrairement à l’hydrogène, les charges du proton et de l’électron y sont inversées. Comme ces antiparticules forment une structure stable et électriquement neutre, l’antihydrogène est bien considéré comme de l’antimatière. En revanche, un positron isolé ou un antineutrino se déplaçant dans l’espace ne sont que des antiparticules, et non de l’antimatière.
Ainsi, même si elles sont étroitement liées, l’antimatière et les antiparticules ne se confondent pas.
L’antimatière est une forme organisée de matière composée d’antiparticules liées, tandis que les antiparticules peuvent aussi exister de façon indépendante, sans constituer de l’antimatière.
La découverte des antiparticules
En 1927, le physicien Paul Dirac entreprend de formuler une équation capable de décrire le comportement des électrons libres de manière cohérente à la fois avec la mécanique quantique et la relativité.
Il y parvient en établissant l’équation suivante :
$$ E^2 - p^2c^2 = m^2c^4 $$
Mais cette équation recelait une particularité troublante : elle admettait deux familles de solutions en énergie :
$$ E = \pm \sqrt{p^2 c^2 + m^2 c^4} $$
La solution positive, $ E = + \sqrt{p^2 c^2 + m^2 c^4} $, apparaissait tout à fait naturelle : elle correspondait à un électron d’énergie positive, comme attendu pour une particule ordinaire.
La solution négative, $ E = - \sqrt{p^2 c^2 + m^2 c^4} $, posait en revanche un vrai casse-tête : elle semblait indiquer l’existence d’électrons dans des états d’énergie négative.
Que se passerait-il si un électron pouvait réellement occuper de tels états ?
Or, selon la mécanique quantique, tout système tend spontanément à abaisser son énergie.
Ainsi, un électron en état d’énergie positive plongerait vers des niveaux plus bas dès qu’une transition lui serait permise.
L’équation de Dirac autorisait une infinité de niveaux d’énergie négative. Si ceux-ci étaient accessibles, un électron y chuterait indéfiniment, émettant un photon à chaque étape.
Le résultat aurait été une instabilité catastrophique : la matière rayonnerait une énergie infinie, jusqu’à s’évanouir.
Pour conjurer ce paradoxe, Dirac formula une hypothèse révolutionnaire : tous les états d’énergie négative sont déjà occupés par des électrons invisibles, formant ce qu’il appela la « mer de Dirac ».
Cette mer emplirait l’univers de façon uniforme, restant indétectable et inerte, sans interagir avec la matière ordinaire.
En revanche, si l’un de ces états venait à se libérer - créant une « lacune » dans la mer - ce vide se comporterait comme une particule d’énergie positive, de charge positive et de masse identique à celle de l’électron.
C’est ainsi qu’apparaît le positron, l’antiparticule de l’électron.
Remarque. Dirac pensa d’abord que ces « trous » pouvaient correspondre aux protons. Il abandonna rapidement cette idée, la masse du proton étant des milliers de fois supérieure à celle de l’électron.
En 1932, Carl Anderson observa expérimentalement le premier positron, confirmant brillamment la prédiction de Dirac.
Cependant, la notion de « mer d’électrons » fut abandonnée dans les années 1940, lorsque Stueckelberg et Feynman réinterprétèrent le positron comme une véritable particule d’énergie positive.
Depuis lors, les positrons sont reconnus comme de vraies particules, et non plus comme de simples « trous » dans un milieu hypothétique.
Cette avancée ouvrit la voie à une idée générale : chaque particule doit posséder une antiparticule correspondante, de même masse mais de charge opposée.
Dans les années 1950, les expériences menées au Bevatron de Berkeley confirmèrent cette vision avec la découverte de l’antiproton et de l’antineutron.
La symétrie de croisement
La symétrie de croisement est un principe selon lequel on peut déduire de nouveaux processus, équivalents à un processus connu, en remplaçant une particule par son antiparticule et en la déplaçant de l’autre côté de l’équation de réaction.
Il s’agit d’une symétrie fondamentale en physique des particules :
Exemple
La diffusion Compton et l’annihilation électron-positron sont reliées par cette symétrie.
La diffusion Compton est un processus bien connu, aisément observable en laboratoire :
$$\gamma + e^- \rightarrow \gamma + e^-$$
Un photon ($\gamma$) heurte un électron libre, se diffuse (en changeant de direction et de longueur d’onde) et l’électron est dévié.
Il s’agit de l’exemple type d’une diffusion : particule + particule $\;\to\;$ particule + particule.
La symétrie de croisement affirme que si un processus est possible, d’autres le sont aussi - du moins théoriquement - obtenus en transférant des particules d’un côté à l’autre de l’équation et en les remplaçant par leurs antiparticules.
Reprenons la diffusion Compton :
$$ \gamma + e^- \rightarrow \gamma + e^- $$
En appliquant la symétrie de croisement, on la transforme en un processus équivalent.
On commence par déplacer le photon initial à droite, en le remplaçant par son antiparticule - qui est encore un photon, puisqu’il s’agit d’une particule autoconjuguée :
$$ e^- \rightarrow \gamma + \gamma + e^- $$
Puis on transfère l’électron final $ e^- $ à gauche et on le remplace par son antiparticule, le positron $ e^+ $ :
$$ e^- + e^+ \rightarrow \gamma + \gamma $$
On obtient ainsi le processus d’annihilation électron-positron, également réel et confirmé expérimentalement.
Autrement dit, la symétrie de croisement révèle que, d’un point de vue mathématique, ces deux réactions sont les manifestations d’une même dynamique quantique sous-jacente.
Elle souligne l’unité profonde de la physique : des phénomènes en apparence distincts reposent en réalité sur les mêmes principes fondamentaux.
Remarque. Même si les deux réactions sont liées mathématiquement, elles ne sont pas identiques sur le plan physique. La diffusion Compton ($\gamma + e^- \rightarrow \gamma + e^-$) se produit lorsque des photons se diffusent sur des électrons libres d’un gaz ou d’un métal, tandis que l’annihilation ($e^- + e^+ \rightarrow \gamma + \gamma$) survient lorsque électrons et positrons se rencontrent et s’anéantissent mutuellement. La symétrie concerne la structure théorique, non les conditions expérimentales.
Et ainsi de suite.