Théorie quantique 

La théorie quantique fut introduite en 1900 par le physicien allemand Max Planck, qui cherchait à expliquer la distribution du rayonnement électromagnétique émis par un corps noir, c’est-à-dire un objet idéal capable d’absorber et de réémettre la totalité du rayonnement incident.

Planck avança l’idée que l’énergie n’était pas libérée de manière continue, comme on le croyait alors, mais par « paquets » discrets appelés quanta. L’énergie de chaque quantum est proportionnelle à la fréquence du rayonnement :

$$ E = h \cdot \nu $$

où $h$ désigne la constante de Planck.

Cette idée inaugure le principe de quantification. Autrement dit, un système physique ne peut adopter une valeur d’énergie quelconque, mais seulement des multiples entiers d’une unité fondamentale.

Que signifie quantifier ? Une analogie aide à se représenter l’idée. Les dunes du désert semblent former un flux continu de sable, mais elles sont en réalité composées d’une multitude de grains discrets. De même, des phénomènes apparemment continus à notre échelle (comme l’énergie du rayonnement, le mouvement des électrons ou les vibrations atomiques) se révèlent quantifiés à l’échelle microscopique.

De même, une photographie paraît uniforme de loin, mais un agrandissement révèle une mosaïque de points lumineux : les pixels.

Pourquoi Planck introduisit-il le quantum ?

Dès le début du XXe siècle, on savait que l’énergie émise par un corps chauffé dépend de sa température.

Pour l’étudier dans des conditions idéales, les physiciens définirent le concept de corps noir, un objet qui absorbe et réémet tout le rayonnement incident, indépendamment de sa nature.

Les mesures montraient que, pour une température absolue $T$ donnée, l’énergie émise $E(\lambda)$ se répartit sur les longueurs d’onde $\lambda$ selon une courbe caractéristique, avec un maximum se déplaçant avec la température.

Ces courbes présentent la forme typique d’une « cloche ».

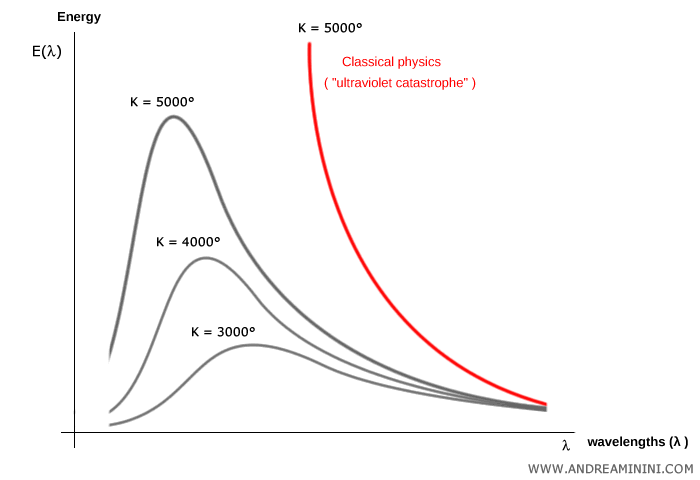
La physique classique, cependant, restait impuissante à expliquer ce comportement. La théorie électromagnétique prédisait qu’un corps noir devait émettre à toutes les fréquences, avec une intensité croissant sans borne aux hautes fréquences.

Ce paradoxe mena à la catastrophe ultraviolette : la prédiction aberrante d’un rayonnement infini aux fréquences élevées.

Certaines lois classiques restaient toutefois valides. Par exemple, la loi de Stefan-Boltzmann énonce que la puissance totale émise par un corps noir est proportionnelle à la quatrième puissance de sa température :

$$ E = \sigma T^4 $$

où $\sigma$ est la constante de Stefan-Boltzmann.

La difficulté essentielle était donc de comprendre comment l’énergie se distribue selon les longueurs d’onde.

Pour y répondre, Planck formula une hypothèse révolutionnaire : l’énergie électromagnétique n’est pas continue, mais délivrée par paquets discrets, les quanta. C’est ainsi qu’intervient la constante de Planck.

Qu’est-ce que la constante de Planck ?

Si l’énergie est quantifiée, elle ne peut varier de manière continue, mais seulement par multiples entiers d’une unité fondamentale.

D’après Planck, l’énergie d’un rayonnement de fréquence $\nu$ est :

$$ E = h \nu $$

où :

• $E$ est l’énergie d’un quantum,
• $\nu$ la fréquence du rayonnement,
• $h$ la constante de Planck, soit environ $6.626 \times 10^{-34} \, \mathrm{J \cdot s}$.

La constante $h$ est une constante universelle qui fixe l’échelle minimale de « granularité » de l’énergie. Elle n’est pas un quantum en soi, mais le facteur qui relie l’énergie d’un quantum à la fréquence correspondante.

De la formule à la loi de Planck

Sur cette base, Planck déduisit l’équation donnant la distribution spectrale de l’énergie émise par un corps noir :

$$ E(\nu) = \frac{8 \pi h \nu^3}{c^3} \cdot \frac{1}{e^{h\nu/kT}-1} $$

où $c$ est la vitesse de la lumière, $k$ la constante de Boltzmann et $T$ la température absolue.

Cette loi rend compte des courbes en cloche observées expérimentalement et résout la catastrophe ultraviolette de la physique classique.

Elle unifie en outre deux résultats partiels : la loi de Rayleigh-Jeans (basses fréquences) et la loi de Wien (hautes fréquences).

En définitive, la constante de Planck marque la limite entre la physique classique et la physique quantique : au-delà de cette échelle, les phénomènes cessent d’être continus et se révèlent quantifiés.

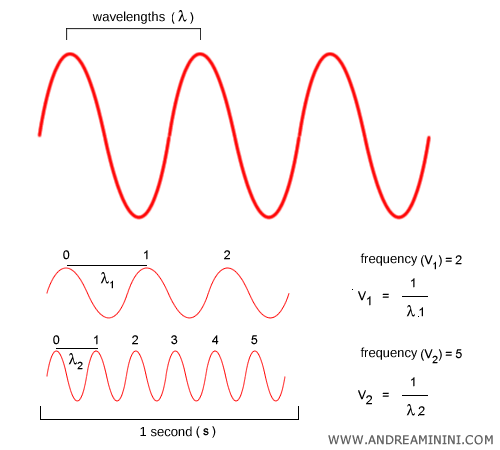
Fréquence et longueur d’onde. La fréquence $\nu$ et la longueur d’onde $\lambda$ sont deux façons équivalentes de décrire une onde : $$ c = \lambda \nu $$ La fréquence ($\nu$) indique le nombre d’oscillations par seconde. La longueur d’onde ($\lambda$) est la distance entre deux crêtes successives. Plus la fréquence est grande, plus la longueur d’onde est courte, et inversement.

Pour illustrer cette échelle microscopique, imaginons un électron en orbite autour du noyau d’un atome d’hydrogène sur une trajectoire circulaire (2πr).

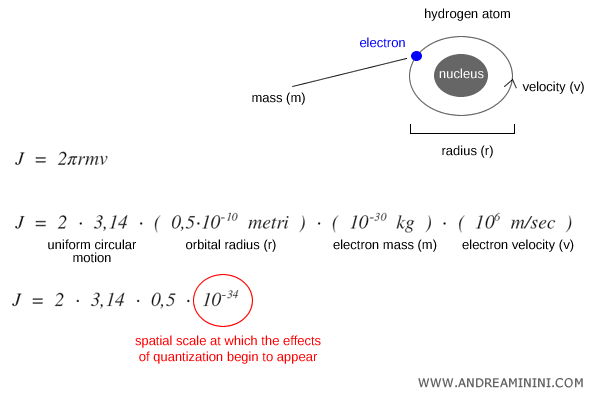
Pour un électron de masse $m \approx 9.1 \times 10^{-31}\,\text{kg}$, de rayon orbital $r \approx 0.5 \times 10^{-10}\,\text{m}$ et de vitesse $v \approx 10^6\,\text{m/s}$, le moment angulaire vaut :

$$ J = 2 \pi r m v \sim 10^{-34} \, \text{J·s} $$

Un ordre de grandeur qui correspond à celui de la constante de Planck $h$.

À cette échelle, la mécanique classique perd sa validité ; la quantification des niveaux d’énergie (modèle de Bohr, mécanique quantique) devient essentielle.

Quanta et ondes électromagnétiques : la différence

Dans la théorie électromagnétique classique, la lumière est envisagée comme une onde continue répartissant son énergie de manière uniforme sur le spectre des fréquences.

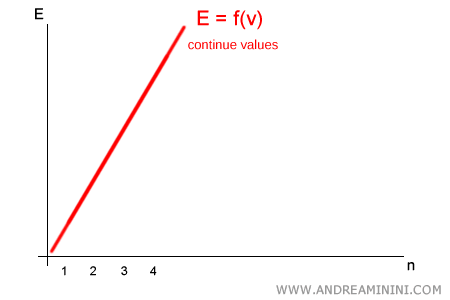
Planck soutint au contraire que l’énergie n’était pas continue : elle ne peut prendre que des valeurs discrètes, multiples entiers du quantum élémentaire $h\nu$. Autrement dit :

$$ E = n \cdot h\nu \qquad (n = 1,2,3,\dots) $$

Il n’existe aucune valeur intermédiaire entre $1 \cdot h\nu$ et $2 \cdot h\nu$ : un système ne peut émettre ou absorber qu’un nombre entier de quanta.

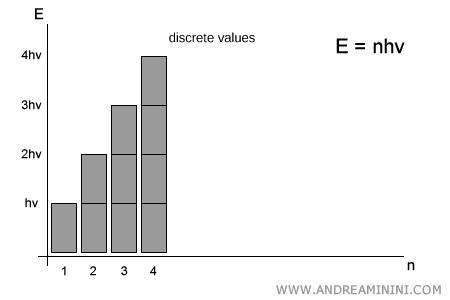
Cette vision introduisit une conception nouvelle de la lumière : non seulement onde, mais aussi flux de particules, les photons, chacun portant une énergie $h\nu$.

La description ondulatoire ne fut pas pour autant abandonnée : les deux modèles, onde et particule, restent valides et se complètent mutuellement.

La dualité onde-particule

Les développements ultérieurs de la mécanique quantique montrèrent que le rayonnement électromagnétique possède une double nature :

• dans certaines expériences, il se comporte comme une onde (interférences, diffraction) ;
• dans d’autres, comme une particule (effet photoélectrique, chocs avec des électrons).

C’est ce qu’on appelle la dualité onde-particule. Les deux aspects coexistent et se manifestent selon le dispositif expérimental.

Et ce phénomène ne se limite pas à la lumière : électrons, protons et neutrons révèlent eux aussi des propriétés ondulatoires, comme l’attestent les expériences de diffraction électronique.

L’effet photoélectrique

L’hypothèse quantique de Planck, formulée en 1900 pour expliquer le rayonnement du corps noir, s’avéra très vite indispensable dans des domaines inattendus.

En 1905, Albert Einstein appliqua l’idée de quantum à l’effet photoélectrique, un phénomène connu depuis la fin du XIXe siècle : lorsqu’une lumière frappe une surface métallique, celle-ci éjecte des électrons.

D’après la théorie électromagnétique classique, l’énergie transportée par la lumière ne dépend que de son intensité, c’est-à-dire de l’amplitude de l’onde.

Dans cette perspective, une lumière suffisamment intense, quelle qu’en soit la couleur, devait pouvoir arracher des électrons à un métal. Or, les expériences révélèrent le contraire :

• Si la fréquence de la lumière ($\nu$) est trop basse (par exemple la lumière rouge), aucun électron n’est libéré, même sous un flux très intense.
• Si la fréquence ($\nu$) dépasse un certain seuil (comme avec les ultraviolets), un faisceau même très faible provoque immédiatement l’émission d’électrons.

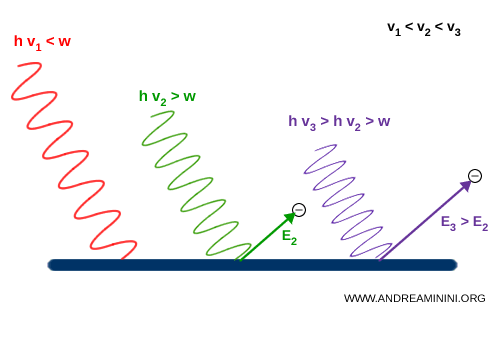
Einstein expliqua ces observations en supposant que la lumière est composée de quanta d’énergie, que nous appelons aujourd’hui photons, chacun portant une énergie bien définie :

$$ E = h \nu $$

Lorsqu’un photon atteint le métal, il peut transmettre son énergie à un électron.

Si cette énergie dépasse la fonction de travail $W$ (l’énergie minimale nécessaire pour extraire un électron), celui-ci est émis. Sinon, rien ne se produit, quelle que soit l’intensité lumineuse.

$$ E_{kin} = h \nu - W $$

Cette interprétation consacra la nature corpusculaire de la lumière, venue compléter son aspect ondulatoire.

Note. Pour cette contribution, Einstein obtint le prix Nobel de physique en 1921. L’effet photoélectrique devint ainsi l’une des preuves expérimentales majeures de la théorie quantique.

Le modèle atomique de Bohr

En 1913, Niels Bohr proposa un modèle atomique novateur afin de surmonter des contradictions que la physique classique laissait irrésolues.

D’après la théorie classique, un électron en orbite autour du noyau devrait rayonner en permanence, perdre progressivement de l’énergie, s’effondrer sur le noyau et rendre impossible l’existence même des atomes.

Bohr formula une idée révolutionnaire : les électrons ne peuvent occuper que certaines orbites stationnaires correspondant à des niveaux d’énergie discrets. Dans ces orbites, ils ne rayonnent pas, assurant ainsi la stabilité de l’atome.

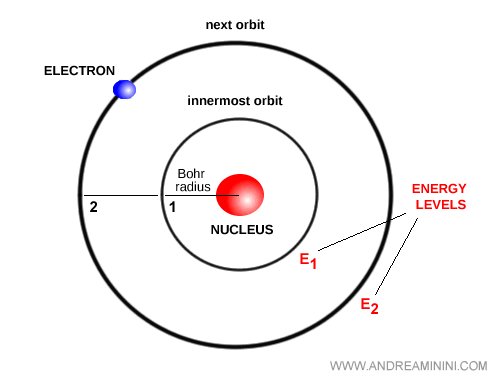
Lorsqu’un électron passe d’un niveau à un autre, l’atome émet ou absorbe un photon dont l’énergie est exactement égale à la différence entre les deux niveaux : $E = h \nu$.

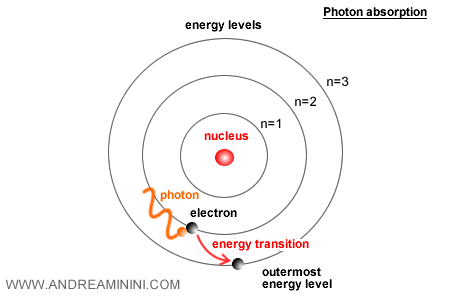
Ce modèle permit à Bohr d’expliquer avec précision le spectre de l’hydrogène, en reproduisant la succession de ses raies spectrales.

Sa contribution fut capitale : il intégra le concept de quantum d’énergie (introduit par Planck et Einstein) au cœur même de la structure atomique, ouvrant la voie à la mécanique quantique.

De la théorie quantique à la mécanique quantique

Dans les années qui suivirent, l’hypothèse quantique s’étendit à de nouveaux phénomènes : les ondes de matière de De Broglie (1924), la mécanique ondulatoire de Schrödinger et la mécanique matricielle de Heisenberg (1925-26).

• L’hypothèse des ondes de matière de De Broglie (1924)
  Louis de Broglie avança que non seulement la lumière, mais aussi les particules matérielles (comme les électrons et les protons), possèdent des propriétés ondulatoires. Chaque particule de quantité de mouvement $p$ est caractérisée par une longueur d’onde : $$ \lambda = \frac{h}{p} $$. Cette idée bouleversante étendait la dualité onde-particule à la matière.
• La mécanique matricielle de Heisenberg (1925)
  En exploitant les données spectroscopiques, Werner Heisenberg élabora un formalisme mathématique fondé sur les matrices plutôt que sur des trajectoires imaginées. Les grandeurs physiques y sont représentées par des opérateurs soumis à des règles de commutation, ce qui conduisit au principe d’incertitude. Rapidement, Born et Jordan codifièrent ce formalisme avec Heisenberg, donnant naissance à la formulation matricielle de la mécanique quantique. Abstraite mais rigoureuse, elle s’avéra équivalente à celle de Schrödinger.
• La mécanique ondulatoire de Schrödinger (1926)
  Erwin Schrödinger introduisit une équation décrivant l’évolution temporelle de la fonction d’onde $\psi$, qui contient toute l’information sur l’état quantique d’un système. L’électron cesse d’y être une particule orbitante pour devenir une onde de probabilité étendue dans l’espace. Les solutions stationnaires de cette équation expliquent les niveaux d’énergie discrets des atomes. Publiée en 1926, cette approche se révéla mathématiquement équivalente à la formulation matricielle de Heisenberg.
• L’interprétation probabiliste de Born (1926)
  Max Born proposa d’interpréter le carré de la fonction d’onde, $|\psi|^2$, comme une densité de probabilité. Cette idée donna à la mécanique ondulatoire son sens physique ; sans elle, elle ne serait restée qu’une construction mathématique abstraite.
• Le principe d’incertitude de Heisenberg (1927)
  Heisenberg formula le principe d’incertitude ($\Delta x \cdot \Delta p \geq \hbar/2$), qui mit en évidence les implications conceptuelles profondes de la nouvelle théorie.
• Dirac et l’unification (1926-1928)
  Paul Dirac joua un rôle central en montrant l’équivalence entre mécanique matricielle et mécanique ondulatoire. En 1928, il publia son équation relativiste de l’électron, qui unifia la mécanique quantique à la relativité restreinte et prédit l’existence de l’antiparticule de l’électron : le positron, mis en évidence expérimentalement par Carl Anderson en 1932.
• La conférence Solvay (1927)
  Organisée à Bruxelles en octobre 1927 sur le thème « Électrons et Photons », elle rassembla les fondateurs de la mécanique quantique. On y retrouvait Planck, Einstein, Bohr, Heisenberg, Schrödinger, Dirac, Born, Pauli, de Broglie, Lorentz, et bien d’autres. La photo de groupe restée célèbre montre 29 participants, dont 17 prix Nobel. Cette conférence consacra la victoire de la mécanique quantique, consacrant les idées de Bohr, Heisenberg, Schrödinger et Born comme cadre de référence. Dans le même temps, Dirac finalisait sa théorie relativiste de l’électron (1928), complétant ainsi le tableau. La physique classique fut dès lors reléguée au rang d’approximation macroscopique, tandis que la physique quantique s’imposait comme la description fondamentale du monde microscopique.

  Le débat Einstein-Bohr. Einstein récusait l’interprétation probabiliste de Born, défendue par Bohr et Heisenberg. Sa phrase fameuse fut : « Dieu ne joue pas aux dés avec l’Univers ». Bohr répliqua qu’il n’appartenait pas à la physique de dicter ses lois à Dieu, défendant l’interprétation de Copenhague. Ce débat sur la nature de la réalité quantique se prolongea des décennies durant.

• Vers la théorie quantique des champs (années 1930-1940)
  Après l’édification de la mécanique quantique « non relativiste », les physiciens s’attaquèrent à l’élaboration d’une théorie des champs relativiste. En résultèrent d’abord la mécanique quantique relativiste, puis l’électrodynamique quantique (QED). La QED considère le rayonnement électromagnétique comme un champ quantifié et décrit avec une précision remarquable les interactions entre électrons, positrons et photons. Elle ouvrit la voie aux théories quantiques des autres forces fondamentales, dont la chromodynamique quantique (QCD) et le modèle standard, et demeure l’un des piliers de la physique moderne.

De cette convergence d’idées émergea la mécanique quantique, un cadre théorique radicalement nouveau qui, à partir des années 1920, bouleversa notre vision du monde microscopique.

La transition de la théorie quantique à la mécanique quantique ne fut pas l’œuvre d’un seul individu, mais le fruit d’un effort collectif auquel participèrent de nombreux scientifiques.

Et l’aventure ne faisait que commencer.