Constante de couplage
En physique théorique, la constante de couplage quantifie l’intensité d’une interaction entre particules.
C’est le paramètre qui détermine dans quelle mesure deux particules se modifient mutuellement par le biais d’une interaction fondamentale.
En d’autres termes : plus la constante de couplage est grande, plus l’interaction est forte.
- Une constante faible correspond à une interaction modérée (par exemple, en QED : $\alpha \approx 1/137$). Dans ce régime, les développements perturbatifs et les séries convergentes sont fiables.
- Une constante élevée indique une interaction intense (par exemple, en QCD à basse énergie : $\alpha_s \sim 1$). Dans ce cas, les méthodes perturbatives perdent leur validité.
Qu’appelle-t-on théorie des perturbations ? C’est un outil mathématique qui permet d’aborder des systèmes autrement inextricables. Lorsque l’interaction est faible, on peut la traiter comme une petite « perturbation » d’un système de référence simple et non interactif. Les méthodes perturbatives ne sont donc pertinentes que si la constante de couplage est suffisamment réduite.
Voici quelques exemples de constantes de couplage associées aux quatre interactions fondamentales :
| Interaction | Constante | Symbole | Valeur typique |
|---|---|---|---|
| Électromagnétique | Constante de structure fine | α | ≈ 1/137 |
| Forte (QCD) | Constante de couplage fort | αs | Variable : ≈ 0.1 - 1 |
| Faible | Constante de Fermi ($G_F$) | - | ≈ 1,166 × 10-5 GeV-2 |
| Gravitation (unités naturelles) | G | - | Extrêmement faible |
La fonction bêta
En théorie quantique des champs, les constantes de couplage ne sont pas véritablement constantes : elles évoluent avec l’échelle d’énergie.
Cette évolution - fonction de l’énergie ou, équivalemment, de la distance - est décrite par la fonction bêta.
En QED (électrodynamique quantique), par exemple, le couplage électromagnétique $ \alpha $ varie avec l’énergie de l’interaction $E$ :
$$ \alpha(E) \ne \alpha(0) \quad \text{(la charge effective croît avec l’énergie)} $$
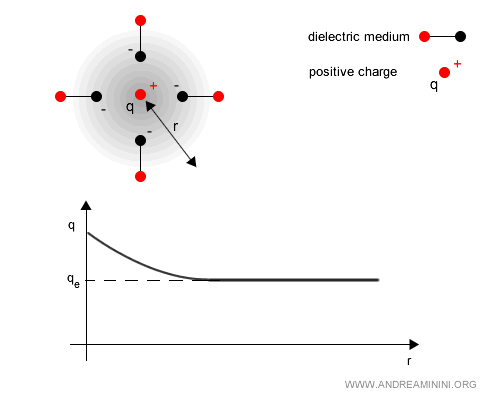
Ce phénomène est connu sous le nom d’écrantage du vide. Sous l’effet des fluctuations quantiques, le vide agit comme un milieu diélectrique qui « masque » partiellement la charge à basse énergie (grandes distances).
À mesure que l’énergie augmente (ou que l’on sonde des distances plus courtes), cet écrantage perd de son efficacité et la charge effective s’accroît.
Exemple. Le vide quantique se comporte comme un diélectrique, car les paires électron-positron virtuelles se polarisent en présence d’une charge. Près d’une charge positive $q$, les électrons virtuels (négatifs) sont attirés, tandis que les positrons (positifs) sont repoussés. Cette redistribution du champ réduit la charge apparente à grande distance. La charge effective $q_e(r)$ mesurée de loin est donc plus faible que la charge nue $q$.
En revanche, en QCD (chromodynamique quantique), le couplage fort $\alpha_s$ diminue avec l’augmentation de l’énergie ou du transfert de moment $Q^2$ :
$$ \alpha_s(Q^2) \downarrow \;\; \text{quand} \;\; Q^2 \uparrow \quad \text{(liberté asymptotique)} $$
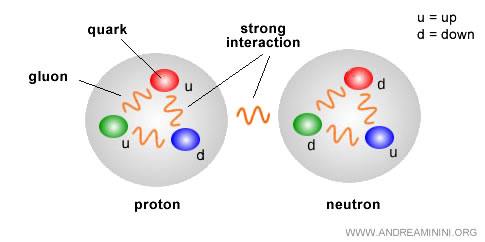
Ce comportement, appelé antiécrantage, provient des auto-interactions des gluons, puisque - à la différence des photons - ils portent eux-mêmes une charge de couleur.
Il en découle qu’à très courte distance (haute énergie), l’interaction entre quarks s’atténue et ceux-ci se comportent presque comme des particules libres à l’intérieur d’un hadron (proton, neutron, etc.). C’est le phénomène de liberté asymptotique.
Inversement, lorsqu’un quark tente de s’échapper d’un hadron, l’interaction avec le champ de couleur croît rapidement, jusqu’à devenir si intense que toute séparation devient impossible. C’est le confinement des quarks.
Remarque. Ce cadre conceptuel est fondamental pour comprendre la liberté asymptotique, l’écrantage du vide et, plus généralement, l’architecture des interactions fondamentales. Il explique, par exemple, pourquoi dans les collisionneurs de haute énergie comme le LHC les quarks semblent interagir faiblement, alors qu’à plus grande échelle le confinement les maintient étroitement liés au sein des hadrons.
Notes complémentaires
Quelques précisions supplémentaires :
- Dans une théorie de jauge (QED ou QCD), la constante de couplage $g$ apparaît explicitement dans le lagrangien : $$ \mathcal{L}_{\text{int}} = g \, \bar{\psi} \gamma^\mu A_\mu \psi $$ où $g$ est la constante de couplage, $A_\mu$ le champ de jauge (photon, gluon) et $\psi$ le champ de matière (électron, quark).
Et ainsi de suite.