La Voie octuple

La Voie octuple est un schéma de classification des particules subatomiques qui regroupe baryons et mésons en familles aux propriétés communes, en s’appuyant sur deux nombres quantiques essentiels :

la charge électrique $Q$
l’étrangeté $S$, un nombre quantique qui traduit la présence de quarks étranges ou d’antiquarks dans la particule.

Ce modèle fut proposé en 1961 par Murray Gell-Mann et, indépendamment, par Yuval Ne’eman, à partir du groupe de symétrie mathématique SU(3).

La Voie octuple visait à mettre de l’ordre dans le fameux « zoo des particules » des années 1950 et 1960, une période où l’on avait identifié des dizaines de particules sans disposer d’un cadre théorique cohérent pour les organiser.

Ces regroupements sont généralement représentés par des figures géométriques régulières, comme des hexagones ou des triangles.

Exemple
Décuplet baryonique

Exemple

Dans le cas des baryons, l’étrangeté $S$ est portée sur l’axe vertical, tandis que la charge électrique $Q$ se lit sur les axes diagonaux.

Cette organisation est connue sous le nom d’octet baryonique.

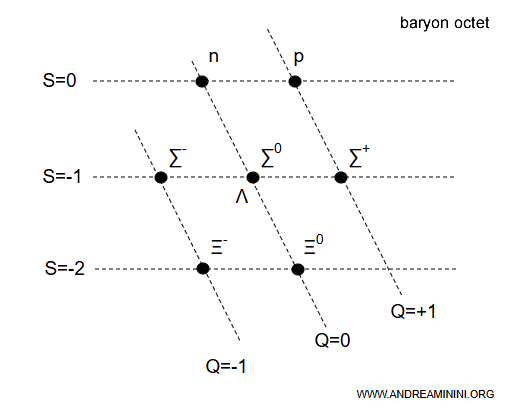
baryon octet diagram

On parle d’« octet » car ce diagramme hexagonal rassemble huit baryons.

Note. Dans ce schéma, les baryons - particules de spin $ \frac{1}{2} $ composées de trois quarks - sont placés selon leur étrangeté ($S$, axe vertical) et leur charge électrique ($Q$, axe horizontal).

En haut, pour $S = 0$, figurent le neutron $n$ (neutre, $Q = 0$) et le proton $p$ (charge positive, $Q = +1$).
Pour $S = -1$, apparaissent les trois baryons $\Sigma$ ($\Sigma^{+}$, $\Sigma^{0}$, $\Sigma^{-}$), accompagnés du baryon $\Lambda$ ($Q = 0$).
En bas, avec $S = -2$, se trouvent les baryons $\Xi$, chacun contenant deux quarks étranges $s$. Le $ \Xi^{-} = (d s s) $ porte une charge négative ($Q = -1$), tandis que le $ \Xi^{0} = (u s s) $ est neutre ($Q = 0$).

Un schéma hexagonal analogue est utilisé pour les mésons.

C’est l’octet des mésons :

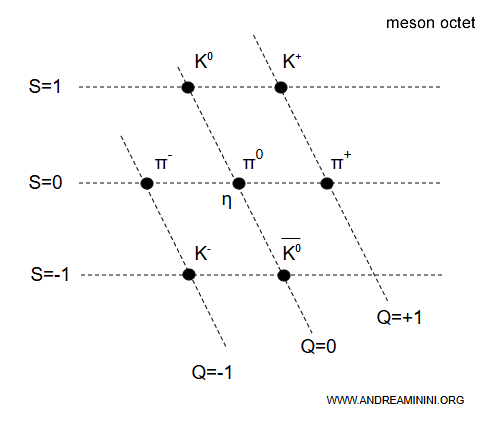
meson octet diagram

Ici, la rangée supérieure correspond à $S = +1$ et la rangée inférieure à $S = -1$, soit l’ordre inverse de celui des baryons.

Note. Ce diagramme représente des mésons pseudoscalaires - particules constituées d’un quark et d’un antiquark - organisés en fonction de leur étrangeté ($S$, axe vertical) et de leur charge électrique ($Q$, axe horizontal).

En haut, avec $S = +1$, se trouvent le kaon neutre $K^{0}$ ($Q = 0$) et le kaon positif $K^{+}$ ($Q = +1$).
Pour $S = 0$, apparaissent les trois pions ($\pi^{-}$, $\pi^{0}$, $\pi^{+}$) ainsi que le méson $\eta$.
En bas, avec $S = -1$, se situent le kaon négatif $K^{-}$ ($Q = -1$) et l’antikaon neutre $\overline{K}^{0}$ ($Q = 0$). Cette répartition illustre la symétrie de saveur $SU(3)$, qui regroupe ces mésons en un octet selon leurs nombres quantiques.

Ces regroupements ont joué un rôle décisif dans l’élaboration de la première classification systématique des particules étranges, en intégrant le nombre quantique d’« étrangeté » introduit dans les années 1950.

Le schéma permit même de prédire des particules encore inconnues - la plus célèbre étant le $ \Omega^- $ (charge $-1$, étrangeté $-3$), mis en évidence en 1964.

Cependant, le modèle présente aussi des limites.

Note. La symétrie n’est qu’approximative, et les masses des particules d’un même multiplet ne coïncident pas exactement. En outre, le modèle ne rend pas compte de l’origine des masses ni de la nature des interactions entre particules.

Malgré ces limites, il a constitué une avancée décisive dans la classification des particules et a ouvert la voie au modèle des quarks, où les baryons de l’octet et du décuplet s’interprètent comme des combinaisons de trois quarks ($u$, $d$, $s$).

Décuplet baryonique

Après l'identification de l'octet baryonique de spin $ \tfrac12 $, les physiciens ont rapidement mis en évidence l'existence d'autres particules aux propriétés très proches, mais caractérisées par un spin intrinsèque plus élevé, égal à $ \tfrac32 $.

Ces nouveaux états ne pouvaient pas être intégrés dans l'octet déjà connu. Leur apparition régulière montrait qu'il ne s'agissait pas de phénomènes isolés, mais de l'expression d'une structure profonde et cohérente, gouvernée par la symétrie SU(3).

D'un point de vue mathématique, la combinaison de trois quarks appartenant à la représentation fondamentale de SU(3) conduit à la décomposition suivante :

$$ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 $$

Dans cette expression, la représentation $10$ correspond au décuplet, la représentation $8$ à l'octet et la représentation $1$ à un singulet.

Autrement dit, l'existence de l'octet implique naturellement celle du décuplet, puisque les deux structures émergent d'une même symétrie fondamentale.

Le décuplet baryonique regroupe des états totalement symétriques dans l'espace des saveurs. Cette symétrie maximale impose que toutes les particules du décuplet possèdent un spin total égal à $ \tfrac32 $.

Contrairement à l'octet, organisé selon une structure hexagonale avec un état central, le décuplet adopte une géométrie triangulaire équilatérale, composée de dix états répartis sur quatre niveaux.

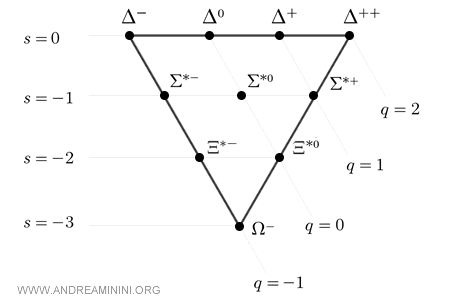
structure du décuplet baryonique

Note. La géométrie triangulaire n'est pas un simple choix de représentation graphique. Elle reflète une propriété physique fondamentale : dans le décuplet, les spins des quarks sont entièrement alignés, ce qui conduit à un spin total égal à $ \tfrac32 $ et à une symétrie interne maximale.

Le diagramme du décuplet est construit à partir de deux nombres quantiques essentiels : l'étrangeté $ S $ et la charge électrique $ Q $. En descendant dans le diagramme, l'étrangeté diminue progressivement, tandis que le nombre de quarks étranges augmente.

Au sommet du triangle se trouvent quatre particules $ \Delta $, dépourvues de quarks étranges et constituées exclusivement de quarks up $ u $ et down $ d $.

$ \Delta^{++} = uuu $
$ \Delta^{+} = uud $
$ \Delta^{0} = udd $
$ \Delta^{-} = ddd $

Juste en dessous apparaissent trois particules $ \Sigma^{*} $, chacune contenant un quark étrange $ s $ et deux quarks légers. L'introduction du quark étrange rompt la symétrie parfaite et se traduit par une augmentation de la masse par rapport aux états $ \Delta $.

$ \Sigma^{*+} = uus $
$ \Sigma^{*0} = uds $
$ \Sigma^{*-} = dds $

Note. L'astérisque indique un état de spin $ \tfrac32 $. La différence entre $ \Sigma $ et $ \Sigma^{*} $ ne réside pas dans leur contenu en quarks, identique dans les deux cas, mais dans la manière dont leurs spins se combinent. Lorsque tous les spins sont alignés (↑↑↑), le spin total vaut $ \tfrac12 + \tfrac12 + \tfrac12 = \tfrac32 $. Lorsqu'ils ne le sont pas complètement (↑↑↓, ↑↓↑, ↓↑↑), le spin total vaut $ \tfrac12 + \tfrac12 - \tfrac12 = \tfrac12 $, et l'état appartient alors à l'octet. Le même raisonnement s'applique aux baryons $ \Xi^{*} $.

Au niveau suivant apparaissent deux particules $ \Xi^{*} $, chacune composée de deux quarks étranges et d'un quark léger. Leur masse est donc plus élevée.

$ \Xi^{*0} = uss $
$ \Xi^{*-} = dss $

À la base du triangle se trouve une seule particule, le $ \Omega^{-} $, constituée exclusivement de quarks étranges :

$$ \Omega^{-} = sss $$

Cette particule occupe le niveau inférieur du décuplet et se caractérise par une étrangeté $ S = -3 $, une charge électrique $ Q = -1 $ et un spin $ \tfrac32 $.

La prédiction du $ \Omega^{-} $. L'un des succès majeurs du modèle des quarks fut la prédiction du $ \Omega^{-} $. Ce baryon complète la structure symétrique du décuplet et, au moment de sa formulation théorique, n'avait pas encore été observé expérimentalement. Sa découverte, en 1964, constitua une confirmation décisive de la symétrie SU(3) et du pouvoir prédictif du modèle des quarks.

Et au-delà.