Les bosons W et Z
Les bosons $W$ et $Z$ sont les particules médiatrices de l’interaction faible, l’une des quatre forces fondamentales de la nature.
À la différence du photon - dépourvu de masse et responsable d’une interaction électromagnétique à portée infinie - les bosons faibles possèdent une masse considérable. Cette particularité confine l’interaction faible à des distances subnucléaires, plus petites encore que la taille d’un noyau atomique.
L’interaction faible se transmet par deux types de bosons :
- Le boson $W$ assure les courants chargés. Il intervient dans les processus où la charge électrique varie et, pour les quarks, où la saveur se modifie. Le boson $ W^+ $ porte une charge positive (+1), tandis que le $ W^- $ porte une charge négative ( - 1). Concrètement, ils peuvent accroître ou réduire la charge d’une particule d’une unité et, simultanément, modifier la saveur de ses quarks.
Un exemple classique est la désintégration bêta : un neutron se transforme en proton en émettant un électron et un antineutrino électronique : $ n \to e^- + \bar{\nu}_e $
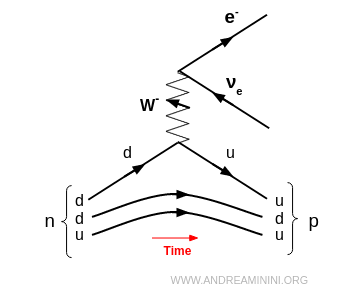
- Le boson $Z$ assure les courants neutres, c’est-à-dire des interactions où aucune particule ne change de charge. Le boson $ Z^0 $, électriquement neutre, ne modifie ni la charge ni la saveur des particules impliquées.
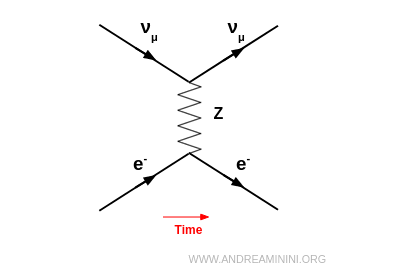
Par exemple, lors d’une diffusion, un neutrino échange un boson virtuel $Z^0$ avec un électron. Tous deux conservent inchangées leur charge et leur saveur : $ \nu_\mu + e^- \;\to\; \nu_\mu + e^- $.
Propriétés essentielles
- Types : $W^+$ et $W^-$ (chargés positivement et négativement) et $Z^0$ (neutre).
- Spin : 1, ce qui les classe parmi les bosons vectoriels (également appelés bosons intermédiaires).
- Masse : environ 80 GeV/$c^2$ pour le $W$, et 91 GeV/$c^2$ pour le $Z$ - plus de 80 fois la masse d’un proton.
- Durée de vie : extrêmement brève, de l’ordre de $10^{-25}$ s ; ils ne peuvent être observés directement, mais uniquement à travers leurs produits de désintégration.
Histoire
Les bosons $ W $ et $ Z $ ont été prédits à la fin des années 1960 par la théorie électrofaible élaborée par Glashow, Weinberg et Salam.
Le défi majeur consistait à comprendre comment ces particules pouvaient acquérir une masse aussi importante sans rompre la cohérence mathématique d’une théorie de jauge.
La solution est venue du mécanisme de Higgs, un processus de brisure spontanée de symétrie qui confère une masse aux bosons $W$ et $Z$, tout en laissant le photon sans masse.
Confirmation expérimentale
Les courants neutres furent observés pour la première fois en 1973 dans l’expérience Gargamelle au CERN, apportant une preuve indirecte de l’existence du boson $ Z^0 $.
L’observation directe des bosons $W$ et $Z$ eut lieu dix ans plus tard, en 1983, également au CERN, grâce aux expériences UA1 et UA2 au Super Proton Synchrotron.
Cette découverte constitua une validation décisive de la théorie électrofaible et valut à Carlo Rubbia et Simon van der Meer le prix Nobel de physique en 1984.
L’étude détaillée des désintégrations du boson $Z$ confirma qu’il existe exactement trois familles de neutrinos dans la nature - et, par conséquent, trois générations de fermions fondamentaux.
Ce résultat demeure aujourd’hui l’un des piliers de notre compréhension du Modèle Standard.
Auto-interactions des bosons $W$ et $Z$
L’un des traits les plus remarquables de l’interaction faible est que ses propres médiateurs ne se limitent pas à transmettre la force : ils interagissent aussi entre eux.
Ce phénomène, qualifié d’auto-interaction, découle naturellement de la structure mathématique de la théorie électrofaible.
Note. L’électrodynamique quantique (QED) est une théorie abélienne : le photon, dépourvu de charge, n’interagit pas avec lui-même. L’interaction faible, en revanche, repose sur le groupe de jauge non abélien $SU(2)_L \times U(1)_Y$. Comme les bosons $W$ portent une charge faible, ils peuvent interagir directement entre eux et avec d’autres bosons du modèle.
Les auto-interactions se présentent sous plusieurs formes :
A] Interactions trilineaires
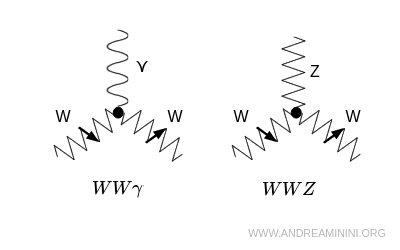
Les sommets trilineaires impliquent trois bosons vectoriels convergeant vers un même sommet de Feynman. Dans le Modèle Standard, les plus importants sont $WW\gamma$ et $WWZ$. Le premier illustre le couplage des bosons chargés $W^\pm$ au photon ; le second atteste de leur lien direct avec le boson neutre $Z^0$.
- $WW\gamma$ : couplage des bosons chargés $W^\pm$ au photon.
- $WWZ$ : interaction des bosons $W$ avec le boson neutre $Z$.
Ces sommets constituent une preuve irréfutable du caractère non abélien de la théorie électrofaible.
B] Interactions quartiques
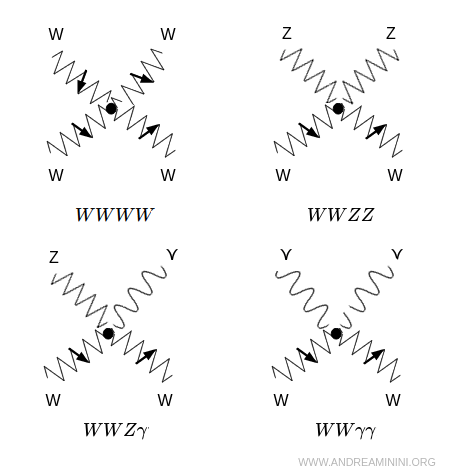
Les sommets quartiques impliquent quatre bosons à la fois - par exemple $WW\gamma\gamma$, $WWZZ$ et $WWZ\gamma$. Moins fréquentes, elles jouent néanmoins un rôle crucial pour garantir l’unitarité des amplitudes de diffusion à haute énergie.
- $WWWW$ : quatre bosons $ W $ interagissant simultanément.
- $WW\gamma\gamma$ : deux bosons $W$ couplés à deux photons.
- $WWZZ$ : deux bosons $W$ couplés à deux bosons $Z$.
- $WWZ\gamma$ : combinaisons mixtes.
Loin d’être accessoires, ces auto-interactions sont essentielles à la cohérence interne de la théorie (en assurant l’unitarité à haute énergie) et distinguent l’interaction faible de la QED, où le photon demeure “inerte”.
Elles ouvrent également la voie à des phénomènes spectaculaires tels que la production multiple de bosons vectoriels lors de collisions à haute énergie.
Note. Ces auto-interactions ont été soumises à des tests approfondis dans les années 1990 au LEP (CERN), où l’on a observé la production de paires $W^+W^-$. Par la suite, les expériences du Tevatron et du Grand collisionneur de hadrons ont confirmé les prédictions du Modèle Standard, en mesurant les sommets trilineaires et quartiques avec une précision remarquable.
Et ainsi de suite.