Théorie des cordes
La théorie des cordes est l'une des idées les plus audacieuses de la physique moderne. Son ambition est immense : unifier toutes les forces fondamentales de la nature, y compris la gravitation, dans un seul cadre cohérent. Autrement dit, comprendre les lois qui régissent tout, du minuscule monde quantique jusqu'à l'immensité cosmique.
Selon cette théorie, tout ce qui compose l'univers - matière, lumière, espace et temps - serait formé non pas de particules ponctuelles, mais de minuscules cordes vibrantes. Ces cordes sont si petites qu'aucun instrument ne pourrait les observer directement. Pourtant, leurs vibrations détermineraient les propriétés des particules élémentaires : chaque mode de vibration donnerait naissance à un type de particule différent.
Bien qu'encore non vérifiée expérimentalement, la théorie des cordes reste l'un des modèles les plus élégants et stimulants jamais proposés pour décrire la structure fondamentale de la réalité.
Réconcilier l'infiniment grand et l'infiniment petit
Depuis plus d'un siècle, la physique repose sur deux piliers qui, malgré leur succès, refusent de s'accorder : la relativité générale d'Einstein et la mécanique quantique.
La première décrit la gravitation et la courbure de l'espace-temps à grande échelle, celle des étoiles, des galaxies et des trous noirs. La seconde régit le comportement du monde microscopique, peuplé d'électrons, de quarks et de photons. Chacune fonctionne à la perfection dans son domaine, mais dès qu'on tente de les combiner, les équations deviennent incohérentes.
La théorie des cordes cherche à combler ce fossé. Elle ambitionne de fournir une théorie du tout, capable d'unifier le cosmos et le monde quantique dans un même langage.
Un univers tissé de cordes
Au lieu de considérer les particules comme des points sans dimension, la théorie imagine qu'elles sont des cordes minuscules qui vibrent selon différents modes.

Un électron, un photon ou un quark ne seraient donc que des cordes vibrantes dans des configurations distinctes.
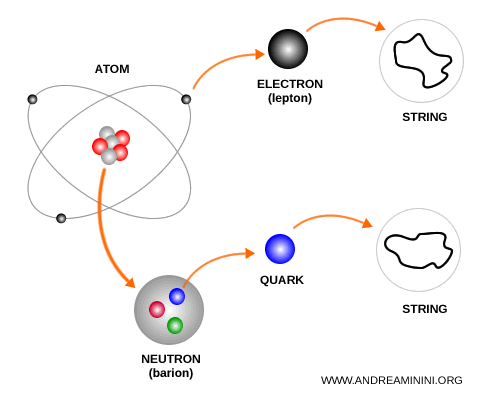
De la même façon que les cordes d'une guitare produisent des notes différentes selon leur tension ou leur longueur, les cordes fondamentales de l'univers généreraient les particules selon leur fréquence vibratoire. La matière et l'énergie apparaîtraient alors comme une immense symphonie cosmique.
Sur le plan mathématique, une corde est décrite par la fonction :
$$ X^{\mu}(\tau, \sigma) $$
où \( \tau \) représente le temps propre et \( \sigma \) la position le long de la corde. Chaque solution de cette équation correspond à un mode de vibration particulier, c'est-à-dire à une particule élémentaire spécifique.
Le graviton : la clé de la gravité quantique
La théorie des cordes prévoit naturellement l'existence du graviton, une particule sans masse et de spin 2, considérée comme le quantum du champ gravitationnel. Si ce graviton existait, il permettrait d'intégrer la gravité au sein de la physique quantique, une étape que les théories précédentes n'ont jamais franchie.
En ce sens, la théorie des cordes pourrait bien être la passerelle tant recherchée vers une unification complète des forces fondamentales de la nature.
Des dimensions cachées
Pour que les équations de la théorie fonctionnent, l'espace-temps doit comporter plus de quatre dimensions. Selon la version envisagée, il en existerait dix dans les théories de supercordes ou vingt-six dans la version bosonique originelle.
Où se cachent ces dimensions supplémentaires ? D'après la théorie, elles sont compactifiées, repliées sur elles-mêmes à des échelles si minuscules qu'elles restent indétectables. L'image souvent utilisée est celle d'un tuyau d'arrosage : vu de loin, il ressemble à une ligne, mais de près, on distingue sa circonférence. De la même manière, l'univers pourrait contenir des dimensions repliées, invisibles à notre regard.
L'histoire de la théorie des cordes
Au début des années 1960, les physiciens se trouvaient face à un des grands mystères de la physique moderne : comprendre la force nucléaire forte et le comportement des hadrons, ces particules composées de quarks. Les modèles de l'époque ne suffisaient plus à expliquer les résultats que les expériences mettaient en évidence. Il fallait repenser les fondations mêmes de la physique des particules.
En 1968, un jeune physicien italien du CERN, Gabriele Veneziano, fit une découverte qui allait tout changer. En utilisant une ancienne fonction mathématique d'Euler, la fonction Bêta, il parvint à décrire avec précision les collisions entre hadrons. La formule semblait sortie de nulle part : personne ne comprenait vraiment pourquoi elle marchait, mais elle reproduisait les données expérimentales avec une justesse impressionnante.
$$ B(x,y)=\int_{0}^{1} t^{,x-1}(1-t)^{,y-1},dt $$
Quelques années plus tard, Yoichiro Nambu, Holger Nielsen et Leonard Susskind proposèrent une idée étonnante : et si les particules élémentaires n'étaient pas des points, mais des cordes vibrantes ? Leurs différents modes de vibration expliqueraient la masse, le spin et d'autres propriétés observées. Un peu comme les cordes d'un violon, dont la note dépend de la manière dont elles vibrent.

Cette idée était aussi audacieuse que géniale, mais elle déroutait. La théorie prédisait des particules sans masse et réclamait des dimensions supplémentaires invisibles à nos yeux. Devant ces difficultés, la communauté scientifique se tourna vers les théories de jauge, qui allaient donner naissance au Modèle standard, le cadre réussi qui décrit aujourd'hui trois des quatre interactions fondamentales.
La renaissance dans les années 1970
En 1974, un détail changea tout. Des calculs plus fins montrèrent qu'un des modes de vibration de la corde correspondait à une particule sans masse et de spin 2 : le graviton, le quantum hypothétique de la gravité. Soudain, la théorie des cordes apparaissait comme le seul cadre capable d'intégrer naturellement la gravitation quantique.
Elle prit alors la forme d'une théorie des cordes bosoniques, ne décrivant que des bosons. Mais cette version exigeait vingt-six dimensions d'espace-temps et souffrait d'une instabilité tachyonique, ce qui la rendait physiquement insoutenable.
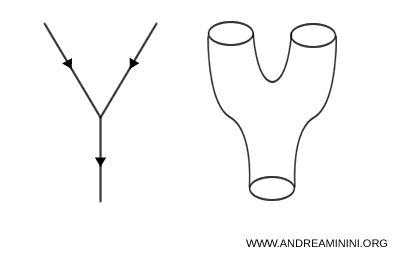
L'introduction de la supersymétrie changea la donne. En liant bosons et fermions, elle donna naissance à la théorie des supercordes, un modèle plus stable, cohérent et limité à dix dimensions.
Dans les années 1980, ce fut la première révolution des supercordes. Les physiciens comprirent que les supercordes pouvaient, en principe, unifier toutes les forces fondamentales, y compris la gravité, et décrire toutes les particules connues comme différents modes de vibration d'une même entité. L'espoir d'une « théorie du tout » semblait enfin à portée de main.
Mais un problème demeurait : il existait cinq versions distinctes de la théorie, toutes valides, toutes cohérentes, mais différentes. Comment pouvaient-elles coexister ?
Les cinq théories de cordes
Au tournant des années 1980 et 1990, la théorie des cordes était devenue le centre de la physique théorique des hautes énergies. Cinq formulations mathématiquement cohérentes furent identifiées :
- Type I
Elle comprend des cordes ouvertes et fermées. Les cordes ouvertes produisent des particules de jauge, les fermées représentent la gravité. Elle possède une symétrie de jauge SO(32) et est supersymétrique. - Type IIA
Constituée uniquement de cordes fermées, elle présente une supersymétrie non chirale, où les deux sens de propagation sont équivalents. Elle est reliée à la supergravitation en dix dimensions et à la théorie M en onze dimensions par compactification. - Type IIB
Également basée sur des cordes fermées, elle possède une supersymétrie chirale, où les deux directions de propagation ont des propriétés distinctes. Elle est reliée à la théorie IIA par des dualités qui échangent charges et dimensions compactifiées. - Hétérotique SO(32)
Elle combine la théorie bosonique et la théorie des supercordes, en liant différents modes de vibration sur les secteurs gauche et droit. Sa symétrie SO(32) assure la cohérence avec la supergravitation en dix dimensions. - Hétérotique E₈×E₈
Similaire à la version SO(32), mais avec un groupe de jauge plus vaste, E₈×E₈. Ce cadre permet de construire des modèles compatibles avec le Modèle standard et les théories de grande unification (GUT).
Malgré ces progrès, nul ne savait comment relier ces cinq théories entre elles. Pourtant, la recherche théorique avança, et les outils mathématiques des cordes gagnèrent en profondeur et en puissance.
La théorie M : une vision unificatrice
En 1995, Edward Witten proposa une nouvelle façon de voir les choses. Il montra que ces cinq théories n'étaient en réalité que des aspects d'un cadre plus vaste en onze dimensions : la théorie M.
Dans cette approche, les cordes deviennent des sections unidimensionnelles d'objets de dimension supérieure appelés branes (du mot anglais membranes), pouvant s'étendre sur deux, trois ou davantage de dimensions spatiales. Selon cette vision, notre propre univers pourrait être une brane vibrante au sein d'un espace à dimensions supérieures, appelé le « bulk ».
Cette idée ouvrit la voie à la seconde révolution des supercordes, qui étendit la notion de corde à des objets multidimensionnels et révéla de profondes correspondances, ou dualités, entre les différentes théories.
Aujourd'hui, la théorie des cordes constitue un cadre unificateur reliant la gravitation quantique, la cosmologie et la physique des particules à haute énergie. Bien qu'aucune preuve expérimentale directe n'ait encore été trouvée, elle reste l'une des approches les plus ambitieuses et fascinantes pour comprendre la structure profonde de l'univers.

Une théorie toujours insaisissable
Aussi élégante soit-elle, la théorie des cordes n’a encore trouvé aucune confirmation expérimentale. Les phénomènes qu’elle décrit se déroulent à des énergies bien trop élevées pour être atteintes par nos instruments actuels, même au sein du Grand collisionneur de hadrons (LHC) du CERN.
Elle reste donc, pour l’instant, une construction purement théorique - une architecture mathématique d’une beauté saisissante, mais encore hors de portée de la vérification empirique.
Remarque. À ce jour, aucune expérience n’a mis en évidence ni les dimensions supplémentaires ni les particules supersymétriques prévues par la théorie. Cela amène certains physiciens à la considérer comme un cadre séduisant, mais difficilement testable avec la technologie actuelle.
Héritage et avenir
Malgré l'absence de preuves directes, la théorie des cordes a profondément transformé la physique théorique. Elle a inspiré de nouveaux outils mathématiques, révélé des liens entre disciplines autrefois séparées et ouvert des perspectives inédites sur les trous noirs, la cosmologie et la gravité quantique.
En somme, la théorie des cordes n'est pas un rêve abandonné, mais une idée en pleine évolution. Elle n'est peut-être pas la clé ultime de l'univers, mais elle demeure l'une des approches les plus fécondes et fascinantes de la recherche moderne.
Et même si elle devait un jour être remplacée, son héritage continuerait d'éclairer la physique du futur. L'exploration, elle, ne fait que commencer.