Coefficient bêta
Le coefficient bêta (ou fonction bêta) décrit l’évolution de la constante de couplage d’une interaction fondamentale lorsque l’on change d’échelle d’énergie : $$ \beta(g) = \mu \frac{d g}{d\mu} $$ où :
- $g$ est la constante de couplage (par exemple, $\alpha$ en QED, $\alpha_s$ en QCD)
- $\mu$ est l’échelle d’énergie (ou l’échelle de renormalisation)
- $\beta(g)$ indique de quelle manière $g$ évolue avec $\mu$ et dans quel sens.
En d’autres termes, le coefficient bêta montre comment une force fondamentale (électromagnétique, forte, etc.) se transforme lorsque l’on sonde des distances plus petites ou des énergies plus élevées.
Il s’agit d’un concept central de la théorie quantique des champs.
La fonction bêta est définie par :
$$ \beta(g) = \mu \frac{d g}{d\mu} $$
Son interprétation physique est immédiate :
- Si $\beta(g) > 0$, l’interaction se renforce avec l’énergie (divergence ultraviolette).
- Si $\beta(g) < 0$, l’interaction s’atténue à mesure que l’énergie croît (liberté asymptotique).
En résumé, le coefficient bêta décrit la manière dont une interaction évolue avec l’échelle d’énergie.
Exemple. En QED, le coefficient bêta est positif, car l’interaction électromagnétique augmente avec l’énergie (effet d’écran). En QCD, au contraire, le coefficient bêta est négatif : l’interaction forte décroît à haute énergie (anti-écrantage). Cette différence est au fondement d’idées clés de la physique moderne, telles que le confinement, la liberté asymptotique ou encore l’évolution des constantes fondamentales de la nature.
Exemple
En électrodynamique quantique (QED), le coefficient bêta est positif :
$$ \beta(\alpha) > 0 $$
Cela signifie que la charge effective croît avec l’énergie, phénomène connu sous le nom de polarisation du vide ou effet d’écran du vide.
À très courte distance (haute énergie), le photon ressent moins de polarisation et la charge paraît plus grande.
À grande distance, les effets de polarisation s’accumulent et la charge effective diminue.
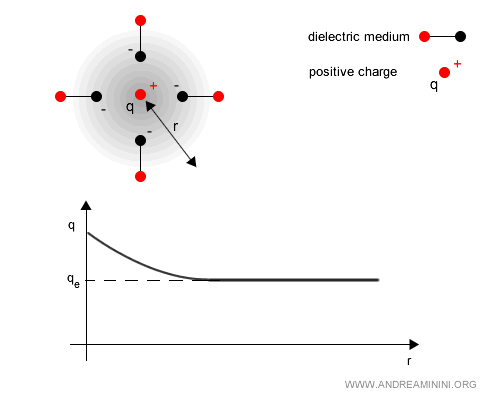
Exemple. Le vide quantique agit comme un milieu diélectrique : les fluctuations engendrent des paires virtuelles électron-positon qui se polarisent en présence d’une charge $ q $. Pour une charge positive, les composantes négatives des paires sont attirées, tandis que les positives sont repoussées. Cette polarisation réduit l’intensité du champ électrique à grande distance, de sorte que la charge effective $q_e(r)$ est inférieure à la charge nue $q$. En d’autres termes, la charge réelle est « écrantée ».
Exemple 2
En chromodynamique quantique (QCD), le coefficient bêta est négatif :
$$ \beta(g_s) < 0 $$
Cela signifie que la constante de couplage décroît avec l’énergie, ce que l’on appelle anti-écrantage.
À très courte distance (énergie élevée), les quarks se comportent presque comme des particules libres (liberté asymptotique).
Inversement, lorsqu’ils s’éloignent les uns des autres, le couplage augmente et les quarks demeurent confinés à l’intérieur des hadrons (protons, neutrons, etc.). Ce phénomène est connu sous le nom de confinement des quarks.
La fonction bêta en QCD
À une boucle, la fonction bêta de la QCD s’écrit :
$$ \beta(g_s) = - \left( \frac{11}{3} N_c - \frac{2}{3} n_f \right) \frac{g_s^3}{16\pi^2} $$
où :
- $N_c = 3$ est le nombre de couleurs
- $n_f$ est le nombre de saveurs de quarks
- $g_s$ est la constante de couplage fort
Le terme $\frac{11}{3}N_c$ provient des gluons virtuels, qui renforcent l’interaction à grande distance (anti-écrantage).
Le terme $\frac{2}{3}n_f$ provient des boucles de quarks virtuels, qui au contraire ont un effet d’écran, comme en QED.
Tant que $n_f < \frac{11}{2}N_c$, le coefficient $ \beta(g_s) $ reste négatif.
Note. Avec trois couleurs $ N_c = 3 $, la condition devient : $$ n_f < \frac{11}{2} \cdot 3 = 16.5 $$ Le comportement dépend donc du nombre de saveurs $ n_f $. S’il y en avait trop, la contribution des quarks dominerait, $ \beta > 0 $, et la liberté asymptotique serait perdue.
En pratique, il existe $ n_f=6 $ saveurs, donc $n_f < 16.5$, et le coefficient bêta de la QCD est bel et bien négatif :
$$ \beta(g_s) < 0 $$
Cela signifie que $g_s$ décroît quand on augmente l’échelle d’énergie.
Autrement dit, en QCD, l’interaction forte s’affaiblit aux très courtes distances.
C’est ce phénomène que l’on appelle liberté asymptotique.
Note. C’est pour cette raison que, lors de collisions d’ultra-haute énergie comme celles du CERN, les quarks se comportent presque comme libres : leur interaction s’atténue à mesure que l’on sonde des échelles de plus en plus élevées.
Une forme simplifiée
En QCD, la fonction bêta à une boucle peut s’écrire de façon compacte (dans des unités convenablement choisies) :
$$ \beta(g) \sim -\left(11n - 2f\right) $$
où $n = N_c$ (nombre de couleurs) et $f = n_f$ (nombre de saveurs).
Dans de nombreuses références, on la trouve sous la forme :
$$ \beta \propto -(11n - 2f) = 2f - 11n $$
ou encore :
$$ \beta \sim (2f - 11n) $$
Les gluons apportent le terme $11N_c$ (anti-écrantage), tandis que les quarks (saveurs) contribuent par le terme $-2n_f$ (écrantage, comme en QED).
En QCD, la fonction bêta reste négative tant que $11n > 2f$, condition qui garantit la liberté asymptotique.
Note. Cette écriture condensée est particulièrement utile pour dégager des tendances générales, notamment pour des valeurs arbitraires de $N_c, n_f$ (par exemple, dans des modèles supersymétriques ou des théories en dimensions supérieures), car elle met clairement en évidence la compétition entre les contributions des gluons et celles des quarks à la fonction bêta.
Et ainsi de suite.