Constante de structure fine

La constante de structure fine, notée $ \alpha $, est une constante fondamentale, pure et adimensionnelle. Sa valeur, proche de $ \alpha = 1/137 $, mesure l'intensité de l'interaction électromagnétique entre particules chargées. Elle est définie par l'expression : \[ \alpha = \frac{e^2}{4 \pi \varepsilon_0 \hbar c} \]

Cette relation repose sur quatre grandeurs essentielles :

• \( e \) : la charge élémentaire
• \( \varepsilon_0 \) : la permittivité du vide
• \( \hbar \) : la constante de Planck réduite
• \( c \) : la vitesse de la lumière dans le vide

La mesure la plus précise de son intensité est :

\[ \alpha \approx \frac{1}{137.035999177} \]

α se distingue par un point essentiel : elle ne dépend d'aucune unité. C'est un nombre pur, une constante universelle qui apparaît partout, des interactions lumière-matière à la structure intime des atomes.

Nota. Au début du XX^e siècle, les physiciens pensaient qu'une transition électronique devait produire une seule ligne spectrale nette. Pourtant, de nombreuses lignes présentaient un dédoublement subtil. Ce phénomène, appelé structure fine, fut expliqué par Arnold Sommerfeld en introduisant des corrections relativistes dans le modèle de Bohr et en formulant explicitement le rôle de la constante $ \alpha $.

Dans le cadre du modèle de Bohr pour l'hydrogène, $ \alpha $ représente à peu près le rapport entre la vitesse de l'électron dans l'état fondamental et celle de la lumière. 

Pourquoi α est-elle si importante ?

α gouverne l'une des forces fondamentales qui structurent la matière. Elle fixe l'intensité de l'attraction coulombienne entre électrons et noyaux, ce qui contrôle la taille des atomes, l'énergie des liaisons chimiques et l'ensemble du comportement de la chimie. Elle intervient aussi dans les réactions nucléaires au cœur des étoiles.

En électrodynamique quantique (QED), α est la constante de couplage qui mesure la force de l'interaction entre un électron et un photon. C'est un paramètre central de la théorie.

Que se passerait-il si $ \alpha $ était plus grande ?

Supposons que $ \alpha $ augmente, par exemple jusqu'à \( 1/110 \). L'attraction électron-noyau serait alors renforcée. Les électrons orbiteraient plus près du noyau et les atomes deviendraient plus compacts.

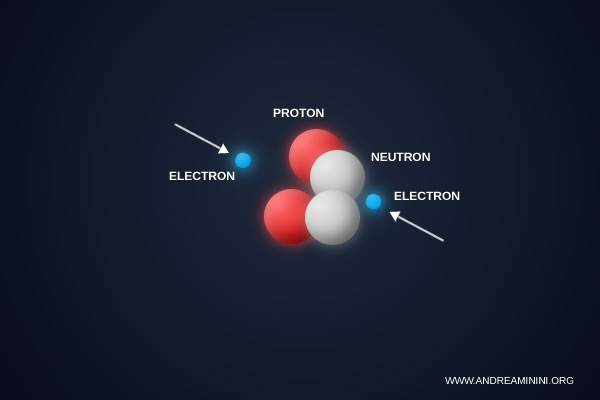
Une telle modification aurait des conséquences profondes. Les liaisons chimiques deviendraient excessivement rigides. La majorité des réactions chimiques seraient bloquées. Par ailleurs, la répulsion accrue entre protons rendrait instables plusieurs noyaux, empêchant la formation de nombreux éléments.

Exemple. Si les liaisons étaient trop solides, les molécules ne pourraient plus se réarranger. La chimie organique s'effondrerait et les processus biologiques cesseraient. La vie, telle que nous la connaissons, ne pourrait pas exister.

Et si $ \alpha $ était plus petite ?

En diminuant α, disons jusqu'à \( 1/200 \), l'attraction entre électrons et noyaux deviendrait plus faible. Les atomes seraient plus grands, moins denses et leur stabilité serait fortement réduite.

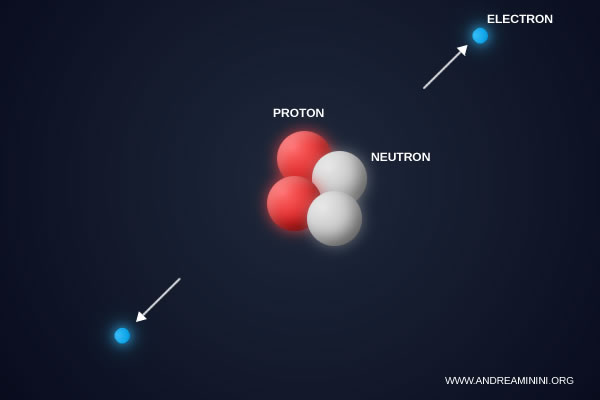
Dans ce scénario, les liaisons chimiques deviendraient trop fragiles pour maintenir des molécules complexes. La chimie organique ne pourrait pas fonctionner.

Exemple. L'eau, les protéines ou l'ADN ne seraient plus stables. Les étoiles seraient incapables de former des éléments essentiels comme le carbone ou l'oxygène, car des processus comme la réaction triple alpha reposent sur des équilibres extrêmement sensibles.

α et l'interaction entre électrons et photons

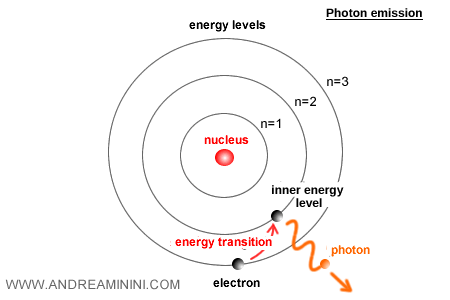
Dans le monde quantique, les électrons échangent de l'énergie avec la lumière en absorbant ou émettant des photons. La probabilité de ces transitions dépend directement de α.

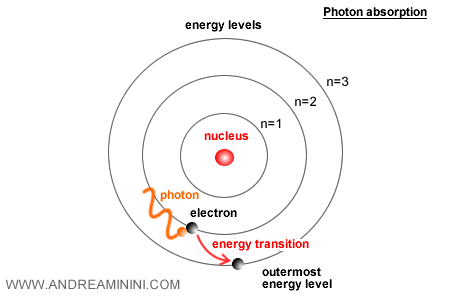
Une valeur trop grande provoquerait un excès de transitions. Une valeur trop faible les rendrait presque impossibles. Le fait que α vaille environ 1/137 permet un équilibre subtil : des spectres atomiques bien définis et des atomes stables.

Points complémentaires

• Évolution de α avec l'énergie
  En QED, la valeur de α dépend de l'échelle d'énergie, un phénomène appelé évolution avec l'énergie (running). À basse énergie, elle vaut environ $$ \alpha \approx \frac{1}{137} $$ mais dans les collisions à très haute énergie, elle peut atteindre $$ \alpha \approx \frac{1}{127} $$ en raison de la polarisation du vide quantique.
• L'hypothèse du multivers
  Certaines théories envisagent l'existence de multiples univers où les constantes fondamentales diffèrent. Notre univers ferait partie de ceux où α adopte une valeur compatible avec une matière stable. Cette idée reste spéculative et non vérifiée expérimentalement.
• Le principe anthropique
  Selon cette approche, nous observons α = 1/137 parce que seuls des univers avec une valeur comparable peuvent accueillir des structures évoluées, capables de mesurer cette constante.

  Nota. Le principe anthropique ne livre pas une explication physique de la valeur de α. Il se limite à souligner un biais de sélection.

• α comme référence universelle
  Parce qu'elle est un nombre pur, identique partout où nous avons pu mesurer la physique, α constitue une référence universelle. Toute civilisation scientifique obtiendrait la même valeur.
  
• Une constante vraiment invariable ?
  Les observations indiquent une remarquable stabilité de α sur des milliards d'années. En 1999, une étude basée sur la lumière de quasars lointains a suggéré une variation possible de l'ordre de $$ \frac{\Delta \alpha}{\alpha} = (-5.7 \pm 1.0) \times 10^{-6} $$ mais ce résultat n'a pas été confirmé. À ce jour, rien ne démontre de manière définitive une variation ou une invariance absolue.

La constante de structure fine demeure un sujet de recherche actif. Chercher à comprendre $ \alpha $, c'est interroger la structure la plus profonde des lois physiques qui gouvernent notre univers.