Les neutrinos

Le neutrino, noté par la lettre grecque $\nu$, est une particule élémentaire appartenant à la famille des leptons. Dépourvu de charge électrique, il possède une masse au repos extraordinairement faible (bien inférieure à celle de toute autre particule de masse non nulle) et un spin de $1/2$, ce qui en fait un fermion.

Ces propriétés lui confèrent un caractère presque « fantomatique » : insensible à l’interaction électromagnétique, étranger à l’interaction nucléaire forte, il traverse la matière pratiquement sans entrave.

Le neutrino n’interagit qu’au moyen de la force nucléaire faible et de la gravité - cette dernière étant négligeable en raison de sa masse infinitésimale.

On les retrouve dans une grande diversité de processus naturels et artificiels : lors de la décroissance bêta des noyaux atomiques et des hadrons, au cœur de la fusion nucléaire des étoiles (notamment celle du Soleil), dans les réacteurs nucléaires, lors des collisions des rayons cosmiques avec l’atmosphère terrestre ou encore dans les accélérateurs de particules.

Remarque. Leur pouvoir de pénétration est saisissant : chaque seconde, des milliards de neutrinos solaires traversent chaque centimètre carré de la surface terrestre sans être stoppés. Au cœur du Soleil, la fusion nucléaire transforme l’hydrogène en hélium en libérant d’innombrables neutrinos électroniques ; environ $ 6.5 \times 10^{10} \ \text{neutrinos} / (\text{cm}^2 \cdot \text{s}) $ atteignent la Terre - ce qui signifie que, chaque seconde, des dizaines de milliards franchissent une surface pas plus grande qu’un ongle, sans laisser la moindre trace.

Pourquoi le terme neutrino

Cette appellation renvoie à leur neutralité électrique et fait écho au neutron - nucléon plus massif présent dans le noyau atomique.

Tout comme le neutrino, le neutron ne porte ni charge positive ni charge négative.

Ce qui distingue neutrinos et neutrons

Le neutron est incomparablement plus lourd et interagit par la force nucléaire forte, tandis que le neutrino ne relève que de la force faible.

La masse exacte du neutrino demeure inconnue. Certaines estimations avancent qu’elle serait environ un million de fois plus faible que celle de l’électron.

D’autres évaluations ne la situent « que » quelques dizaines de milliers de fois en dessous.

Remarque. Si, à titre d’hypothèse, la masse d’un neutrino était un million de fois inférieure à celle de l’électron, et sachant que la masse de l’électron est elle-même 1835 fois plus faible que celle du neutron (voir le noyau atomique), alors le neutrino serait environ deux milliards de fois plus léger qu’un neutron. 

La mesure de la masse du neutrino constitue l’un des grands défis de l’astrophysique contemporaine. La masse totale de l’ensemble des neutrinos de l’Univers pourrait contribuer à éclairer, au moins partiellement, l’énigme de la matière noire.

Propriétés des neutrinos

Le tableau suivant résume de manière synthétique les principales caractéristiques physiques des neutrinos.

Propriété	Valeur / Description
Symbole	ν (neutrino), ν̄ (antineutrino)
Types (saveurs)	νe, νμ, ντ
Nombre leptonique	νe : Le=+1, νμ : Lμ=+1, ν&tau : L&tau=+1 Antineutrinos : saveurs correspondantes avec nombre leptonique -1
Charge électrique	0 (neutre électriquement)
Spin	½ (fermions, soumis aux statistiques de Fermi-Dirac)
Masse au repos	Non nulle mais extrêmement faible (« 1 eV/c2) ; seules les différences de masse ont pu être mesurées, pas les valeurs absolues
Interactions	Force faible (médiée par les bosons W⊃± et Z0) et gravité (négligeable à l’échelle subatomique)
Hélicité / Chiralité	Tous les neutrinos observés sont gauchers ; tous les antineutrinos observés sont droitiers
Oscillations	Peuvent changer de saveur en cours de propagation (mélange PMNS)
Section efficace typique	∼10-44 m2 aux énergies de l’ordre du MeV (valeur croissant avec l’énergie dans ce domaine)
Transparence à la matière	Interagissent si rarement qu’ils traversent des quantités colossales de matière sans diffusion

Les masses absolues des neutrinos restent indéterminées. Seules des bornes supérieures sont établies, toute valeur chiffrée précise relevant pour l’instant de la spéculation. 

Saveurs, antineutrinos et nombres leptoniques

On distingue trois « saveurs » de neutrinos, chacune associée à un lepton chargé correspondant :

Saveur de neutrino	Symbole	Lepton associé
Neutrino électronique	\(\nu_e\)	Électron
Neutrino muonique	\(\nu_{\mu}\)	Muon
Neutrino tauique	\(\nu_{\tau}\)	Tau

Un neutrino créé avec une saveur donnée ne conserve pas nécessairement cette identité au cours de son trajet. Ce phénomène est connu sous le nom d’oscillations des neutrinos.

Chaque neutrino est porteur d’un nombre leptonique bien défini.

Chaque neutrino possède une antiparticule correspondante, appelée antineutrino, qui se caractérise par un nombre leptonique de signe opposé.

Particule	Symbole	Nom	Nombre leptonique
Neutrino électronique	\(\nu_e\)	Neutrino électronique	+1
Neutrino muonique	\(\nu_{\mu}\)	Neutrino muonique	+1
Neutrino tauique	\(\nu_{\tau}\)	Neutrino tauique	+1
Antineutrino électronique	\(\bar{\nu}_e\)	Antineutrino électronique	-1
Antineutrino muonique	\(\bar{\nu}_{\mu}\)	Antineutrino muonique	-1
Antineutrino tauique	\(\bar{\nu}_{\tau}\)	Antineutrino tauique	-1

Neutrinos et antineutrinos interviennent dans une multitude de processus nucléaires, aussi bien naturels qu’expérimentaux.

Exemple

Dans la désintégration bêta⁻, un neutron du noyau se convertit en proton.

Ce processus s’accompagne de l’émission d’un électron et d’un antineutrino électronique :

$$ n \rightarrow p + e^- + \bar{\nu}_e $$

Du côté gauche, le neutron $n$ possède un nombre leptonique nul.

Du côté droit apparaissent :

• un proton $p$ avec $L=0$
• un électron $e^-$ avec $L=+1$
• un antineutrino électronique $\bar{\nu}_e$ avec $L=-1$

Le bilan donne :

$$ 0 + 1 + (-1) = 0 $$

Le nombre leptonique est donc identique des deux côtés : la loi de conservation est respectée.

La réaction est par conséquent autorisée dans le cadre du Modèle standard.

Remarque. Dans la désintégration bêta⁺, le scénario inverse se produit : un proton se transforme en neutron. Ce processus s’accompagne de l’émission d’un positron (l’antiparticule de l’électron) et d’un neutrino électronique : $$ p \rightarrow n + e^+ + \nu_e $$ Là encore, le nombre leptonique se conserve : $$ p^{(0)} \;\rightarrow\; n^{(0)} \;+\; e^{+\,(-1)} \;+\; \nu_e^{(+1)} $$ Pour plus de clarté, le nombre leptonique de chaque particule est indiqué en exposant. La somme des deux côtés reste $0 + (-1) + (+1) = 0$. Cette réaction est elle aussi conforme au Modèle standard.

Pourquoi les neutrinos traversent-ils la matière avec une telle facilité ?

Les neutrinos franchissent la matière avec une aisance remarquable parce qu’ils n’interagissent qu’au moyen de la plus faible des forces fondamentales.

D’un point de vue physique, leur quasi « invisibilité » se comprend à partir de trois facteurs essentiels :

• Interaction faible uniquement
  Dépourvus de charge électrique, les neutrinos échappent complètement à l’électromagnétisme : ils ne sont ni attirés par les protons, ni repoussés par les électrons. Ils ne ressentent que la gravité (insignifiante à l’échelle subatomique) et la force faible, immensément plus faible que la force forte et l’électromagnétisme. De surcroît, la force faible n’agit qu’à très courte portée - environ $10^{-18}$ m - ce qui réduit drastiquement la probabilité qu’un neutrino interagisse avec un nucléon.
• Section efficace dérisoire
  La probabilité d’interaction est décrite par la section efficace ($\sigma$). Pour un neutrino d’énergie typique ($E \approx 1\ \text{MeV}$), elle n’est que de l’ordre de $10^{-44} \ \text{m}^2$, soit des milliards de milliards de fois plus petite que celle d’une particule chargée. Autrement dit, un neutrino pourrait traverser plusieurs années-lumière de plomb compact sans subir la moindre interaction.
• Masse infime
  Bien que non nuls, leur masse est si réduite (inférieure à $1\ \text{eV}/c^2$) qu’ils se déplacent pratiquement à la vitesse de la lumière. Ce mouvement quasi luminal leur laisse encore moins d’occasions d’interagir : ils ne « restent » jamais assez longtemps auprès des nucléons pour réagir.

  Ainsi, sur Terre, près de 60 milliards de neutrinos solaires traversent chaque centimètre carré de matière chaque seconde - quasiment tous sans la moindre interaction.

Pris ensemble, ces facteurs expliquent pourquoi la probabilité d’interaction d’un neutrino avec la matière est extraordinairement faible.

 

Contexte historique

En 1930, Wolfgang Pauli remarqua que le processus de désintégration bêta semblait enfreindre la loi de conservation de l’énergie.

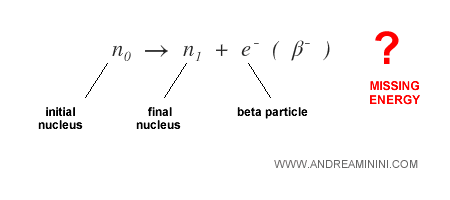
Seule une partie de l’énergie excédentaire apparaissait sous forme de particule bêta ; le reste semblait se volatiliser - ce qui est inconcevable selon les lois de la physique.

Pour résoudre cette énigme, Pauli postula l’existence d’une particule nouvelle - neutre électriquement et de masse extrêmement faible - capable d’emporter l’énergie manquante lors de la désintégration β.

Remarque. Pauli observa qu’un noyau radioactif $A$ pouvait se transformer en un noyau légèrement plus léger $B$, en émettant un électron $e^-$ : $$ A \rightarrow B + e^-$$ Toutefois, la conservation de la charge impliquait que le noyau $B$ devait avoir une charge positive supérieure à celle de $A$, ce que les données expérimentales de l’époque ne confirmaient pas. Le neutron n’était pas encore découvert. De plus, l’énergie des électrons émis était systématiquement inférieure à celle prédite par la conservation de l’énergie.

En 1934, Enrico Fermi reprit l’idée de Pauli, formula sa théorie de la désintégration bêta et baptisa « neutrino » ce que l’on appelait jusque-là la « particule de Pauli ».

Dans le modèle de Fermi, un neutron se transforme en proton, électron et antineutrino électronique :

$$ n \rightarrow p^+ + e^- + \bar{\nu}_e $$

Remarque. Le terme « neutrino » aurait été forgé à la fois sérieusement et sur un ton malicieux, comme diminutif de « neutron », lors d’une conversation entre Enrico Fermi et Edoardo Amaldi à l’institut de physique de la Via Panisperna, à Rome.

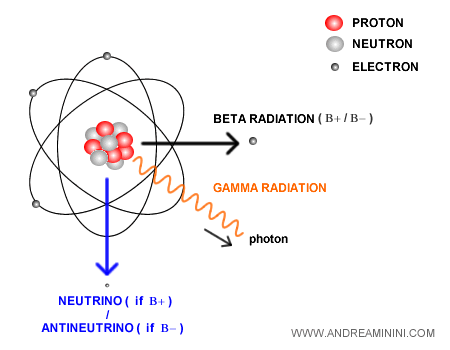
On établit par la suite qu’il existe deux grandes catégories de neutrinos :

1. Le neutrino apparaît dans la désintégration β⁺, accompagné d’un positron $e^+$. Dans ce cas, un proton d’un noyau instable se transforme en neutron, en émettant un positron et un neutrino électronique : $$ p \;\longrightarrow\; n + e^+ + \nu_e $$ L’inverse correspond à l’absorption d’un antineutrino électronique : $$\bar{\nu}_e + p \to n + e^+$$

   Remarque. Un proton libre ne peut pas subir de désintégration β⁺ en raison des contraintes énergétiques (le neutron étant plus massif), mais ce processus devient possible dans un noyau où la différence de masse nucléaire compense cet écart.

2. L’antineutrino est produit lors de la désintégration β⁻, accompagné de l’émission d’un électron $e^-$. Dans ce cas, un neutron - libre ou lié - se convertit en proton, en émettant un électron et un antineutrino électronique : $$ n \;\longrightarrow\; p + e^- + \bar{\nu}_e $$ L’inverse correspond à l’absorption d’un neutrino électronique : $$\nu_e + n \to p + e^-$$

À partir de 1949, on sut aussi que les pions $ \pi^- $ se désintègrent en muons et neutrinos, et que les muons $ \mu^- $ se désintègrent eux-mêmes en un électron ($ e $) et deux neutrinos ($ 2 \nu $) :

$$ \pi^- \rightarrow \mu^- + \nu $$

$$ \mu^- \rightarrow e^- + 2\nu $$

En 1953, Konopinski et Mahmoud formulèrent explicitement le principe de conservation du nombre leptonique dans toutes les interactions de particules.

Remarque. Selon ce principe, $L = +1$ est attribué à tous les leptons (électron, muon, tau et leurs neutrinos), $L = -1$ à tous les antileptons (positron, antimuon, antitau et antineutrinos), et $L = 0$ à toutes les autres particules. Une interaction n’est possible que si la somme des nombres leptoniques reste identique avant et après la réaction.

Au début des années 1950, le neutrino était largement accepté sur le plan théorique, mais aucune observation directe n’avait encore été réalisée - certains allaient jusqu’à douter de sa réalité physique.

La première détection formelle intervint en 1956, lorsque Cowan et Reines mirent en évidence l’antineutrino électronique par désintégration bêta inverse :

$$ \bar{\nu} + p^+ \rightarrow n + e^+ $$

À la fin des années 1950, une question surgit : neutrinos et antineutrinos ne seraient-ils pas en fait une seule et même particule, puisqu’ils partagent la neutralité électrique ?

En 1958, Raymond Davis apporta la preuve expérimentale que neutrinos et antineutrinos sont bel et bien distincts, confirmant ainsi les prédictions liées à la conservation du nombre leptonique.

Exemple. La réaction suivante est permise car la somme des nombres leptoniques (indiqués en exposant) est la même des deux côtés : $$\bar{\nu}^{(-1)} + p^{+(0)} \;\longrightarrow\; n^{(0)} + e^{+( -1 )} $$ En revanche, la réaction suivante est interdite car le bilan ne se conserve pas : $$ \nu^{(+1)} + p^{+(0)} \;\longrightarrow\; n^{(0)} + e^{+( -1 )} $$ Ce contraste illustre clairement la distinction fondamentale entre neutrinos et antineutrinos.

En 1962, une expérience conduite par Lederman, Schwartz et Steinberger apporta la première preuve directe de l’existence de deux « saveurs » distinctes de neutrinos : le neutrino électronique et le neutrino muonique.

Une fois reconnues les différences entre neutrinos et antineutrinos - ainsi que leurs diverses saveurs - on put écrire les désintégrations des pions ainsi :

$$ \pi^- \rightarrow \mu^- + \bar{\nu}_\mu $$

$$ \pi^+ \rightarrow \mu^+ + \nu_\mu $$

Les désintégrations des muons s’écrivent alors :

$$ \mu^- \rightarrow e^- + \bar{\nu}_e + \nu_\mu $$

$$ \mu^+ \rightarrow e^+ + \nu_e + \bar{\nu}_\mu $$

Oscillation des neutrinos

L’oscillation des neutrinos est un phénomène quantique par lequel un neutrino (électronique, muonique ou tauique) peut changer de saveur au cours de sa propagation dans l’espace.

En d’autres termes, un neutrino électronique peut se transformer en neutrino muonique ou tauique, et inversement.

À ce jour, on distingue trois types (ou saveurs) de neutrinos :

• $ \nu_e $ (neutrino électronique)
• $ \nu_{ \mu } $ (neutrino muonique)
• $ \nu_{ \tau } $ (neutrino tauique)

Ces neutrinos possèdent des masses différentes - minuscules, certes, mais bel et bien non nulles.

L’essentiel est qu’aucun d’eux ne correspond à un état de masse unique. Chacun constitue en réalité une superposition quantique des trois états de masse \(\nu_1, \nu_2, \nu_3\), associés respectivement aux masses propres \(m_1, m_2, m_3\).

$$ \begin{bmatrix} \nu_e \\ \nu_\mu \\ \nu_\tau \end{bmatrix} = U \begin{bmatrix} \nu_1 \\ \nu_2 \\ \nu_3 \end{bmatrix} $$

Ici, \(U\) désigne la matrice PMNS (Pontecorvo-Maki-Nakagawa-Sakata), qui encode les angles de mélange ainsi que les phases.

Il en résulte qu’un neutrino produit initialement comme \(\nu_e\) est en réalité une combinaison des trois états de masse. Au cours de sa propagation, chacun de ces états évolue avec une phase différente. La composition se modifie donc avec le temps, de telle sorte qu’un neutrino peut finalement être détecté comme \(\nu_\mu\) ou \(\nu_\tau\), c’est-à-dire avec une saveur différente de celle d’origine.

Les expériences ont confirmé ce phénomène de manière irréfutable.

Remarque. Ce mécanisme a permis de résoudre le fameux « problème des neutrinos solaires » : l’étonnante rareté des neutrinos électroniques solaires par rapport aux prédictions théoriques. L’explication est que beaucoup d’entre eux oscillent en neutrinos muoniques ou tauiques durant leur voyage du Soleil jusqu’à la Terre.

L’existence même de cette oscillation prouve que les neutrinos possèdent une masse non nulle - une découverte majeure, puisque la version initiale du Modèle standard les considérait comme des particules dépourvues de masse.

Et l’histoire se poursuit…