Lois de conservation en physique subatomique

Une loi de conservation est un principe fondamental de la physique selon lequel certaines grandeurs essentielles - telles que l’énergie, la quantité de mouvement, la charge électrique ou le nombre baryonique - demeurent invariantes dans tout processus naturel, quelles que soient les transformations survenues dans le système.

Autrement dit, ces grandeurs peuvent changer d’aspect ou se redistribuer entre les particules en interaction, mais leur valeur totale reste identique avant et après le processus. Toute évolution physique doit respecter ces lois de conservation.

Ces principes constituent la pierre angulaire de la physique des particules : ils déterminent quelles réactions sont réalisables, quelles désintégrations se produisent effectivement et lesquelles sont rigoureusement interdites.

Exemple. Dans la désintégration bêta, un neutron se transforme en un proton, un électron et un antineutrino électronique : $$ n \;\to\; p^+ + e^- + \bar{\nu}_e $$ Le neutron est électriquement neutre. Après la désintégration, le proton porte une charge +1, l’électron -1 et le neutrino 0. Le bilan est $+1 - 1 + 0 = 0$ : la charge initiale est donc conservée. $$ n^{(0)} \;\to\; p^{+(+1)} + e^{(-1)} + \bar{\nu}_e^{(0)} $$

Certaines de ces lois de conservation sont absolues, comme celles de la charge électrique, du nombre baryonique ou de l’énergie.

D’autres ne s’appliquent que sous certaines conditions, comme la conservation de la saveur ou la règle OZI, qui expliquent pourquoi certains processus de désintégration sont extrêmement rares, voire pratiquement absents.

Lois de conservation dans les interactions fondamentales

Voici les principales lois de conservation qui régissent le comportement des particules élémentaires :

• Conservation de la charge électrique
  La somme des charges des particules initiales doit être égale à celle des particules finales. Cette loi est universelle et vaut dans toutes les interactions fondamentales : forte, électromagnétique et faible.

  Exemple : Dans un sommet d’interaction faible, $$ \nu_e \to e^- + W^+ $$ la charge initiale est 0 (celle du neutrino), tandis que la charge finale correspond à l’électron (-1) plus celle du boson $W^+$ (+1), soit -1 + 1 = 0. Le bilan est exact : la charge se conserve.

• Conservation de la couleur (QCD)
  Dans les interactions fortes, la couleur des quarks (rouge, vert, bleu) peut varier, mais le gluon transporte toujours la différence. Comme toutes les particules observables sont neutres en couleur (blanches), la règle est simple : ce qui entre nul doit ressortir nul. Aucune particule isolée ne peut exister avec une charge de couleur non compensée.

  Exemple. Un proton est formé de trois quarks (rouge + vert + bleu) : $$ u_r + u_g + d_b $$ Si l’un des quarks change de couleur en émettant un gluon, ce dernier emporte la différence, garantissant que le proton reste globalement incolore.

• Conservation du nombre baryonique
  Le nombre baryonique total demeure constant dans toute interaction. Chaque quark contribue pour +1/3, chaque antiquark pour -1/3. Ainsi, les baryons (trois quarks) valent +1, les antibaryons (trois antiquarks) -1 et les mésons (paires quark-antiquark) 0. Les baryons et antibaryons n’apparaissent ni ne disparaissent isolément : ils sont toujours créés ou détruits par paires. C’est l’une des lois les plus robustes, jamais mise en défaut, et elle fonde la stabilité du proton.

  Exemple. Cette réaction respecte la conservation du nombre baryonique : $$ p + \bar{p} \;\to\; \pi^+ + \pi^- $$ Le proton (p) a $+1$, l’antiproton $-1$, et les pions 0. Les états initial et final totalisent donc chacun 0. $$ p^{(+1)} + \bar{p}^{(-1)} \;\to\; \pi^{+(0)} + \pi^{-(0)} $$ Le nombre baryonique est conservé.

• Conservation des nombres leptoniques
  Il existe trois nombres leptoniques indépendants : l’électronique $L_e$, le muonique $L_\mu$ et le tauonique $L_\tau$. Chacun se conserve séparément dans les interactions fondamentales, sauf lors des oscillations de neutrinos où un type peut se convertir en un autre. Seuls les leptons portent un nombre leptonique ; toutes les autres particules valent zéro. Par exemple, $L_e$ vaut +1 pour l’électron et le neutrino électronique, et -1 pour leurs antiparticules.
  
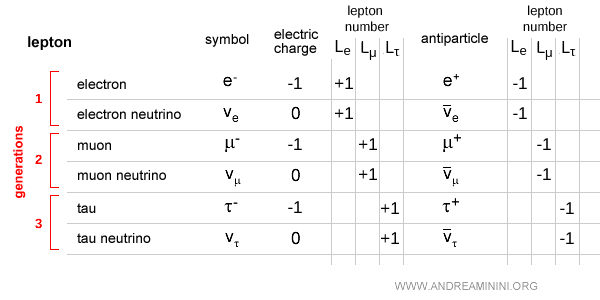
  Les quarks, en revanche, ne suivent pas une loi stricte de conservation par génération, car les interactions faibles mélangent naturellement les saveurs de quarks via la matrice CKM.

  Exemple. Un cas typique est la désintégration du pion chargé : $$ \pi^- \;\to\; \mu^- + \bar{\nu}_\mu $$ En attribuant les nombres leptoniques : $$ \pi^{- (0)} \;\to\; \mu^{- (L_\mu = +1)} + \bar{\nu}_\mu^{(L_\mu = -1)} $$ La somme initiale est $0$, et la somme finale $+1 + (-1) = 0$. Le nombre leptonique muonique $L_\mu$ est conservé.

• Conservation approchée de la saveur
  La conservation de la saveur n’est pas universelle ; elle dépend du type d’interaction :
  • Dans les interactions fortes et électromagnétiques, les saveurs des quarks (up, down, strange, charm, bottom, top) sont strictement conservées.
  • Dans les interactions faibles, en revanche, les saveurs peuvent changer : un quark peut se transformer en un autre ($u \to d$, $s \to u$, etc.).
  L’étrangeté - et plus généralement les saveurs de quarks - n’est donc conservée qu’approximativement. Cela explique pourquoi les particules étranges apparaissent en paires et se désintègrent lentement, contraintes de le faire par interaction faible.

  Exemple. Dans les interactions fortes, les particules étranges se forment toujours par paires $s$ - $\bar{s}$, préservant l’étrangeté totale. Lors des désintégrations, en revanche, un quark étrange peut changer de saveur grâce à l’interaction faible, ce qui explique la relative lenteur des désintégrations de particules étranges.

• Règle OZI (Okubo - Zweig - Iizuka)
  Certaines désintégrations, bien que cinématiquement possibles, sont observées comme extraordinairement rares. Cela se produit lorsque le diagramme de Feynman du processus peut être « coupé » en deux en séparant uniquement des lignes de gluons (sans couper de lignes de particules réelles). Dans ces cas, la désintégration n’est pas strictement interdite, mais elle est fortement supprimée : sa probabilité devient quasi nulle.

À ces lois s’ajoutent les lois cinématiques plus « évidentes » de la physique :

• Conservation de l’énergie
  L’énergie totale d’un système isolé ne peut ni croître ni diminuer ; elle ne peut que se transformer d’une forme en une autre.
• Conservation de la quantité de mouvement
  En l’absence de forces extérieures, la quantité de mouvement totale d’un système reste constante, même si les particules changent de direction ou de vitesse.
• Conservation du moment angulaire
  Si aucun couple externe n’agit sur le système, le moment angulaire total - orbital et de spin - demeure invariable tout au long de l’interaction.

Et la liste pourrait encore s’allonger.