Le spin en mécanique quantique

Le spin est l'une des propriétés les plus fascinantes de la physique quantique. Chaque particule élémentaire en possède un et, avec des grandeurs comme l'énergie ou le moment angulaire orbital, il permet de définir complètement son état quantique. C'est une notion incontournable pour comprendre la structure de la matière.

Contrairement à ce que son nom pourrait laisser penser, le spin n'est pas une rotation réelle de la particule autour d'un axe. Il s'agit d'une propriété intrinsèque, une sorte de signature quantique, qui n'a pas d'équivalent mécanique dans notre expérience quotidienne.

D'un point de vue mathématique, le spin partage certaines caractéristiques avec le moment angulaire classique, notamment ses dimensions physiques. Mais cette analogie ne doit pas être prise au pied de la lettre. Elle sert surtout à guider l'intuition dans un domaine où les objets n'ont pas d'extension spatiale mesurable.

Exemple. L'électron est traité comme une particule ponctuelle, sans structure interne. L'imaginer tournant sur lui-même comme une petite boule ne correspond à aucun phénomène physique réel.

Une particularité essentielle du spin est qu'il ne peut prendre que des valeurs quantifiées. Autrement dit, il ne varie pas continûment mais seulement par pas de taille déterminée :

$$ s = 0,\ \tfrac{1}{2},\ 1,\ \tfrac{3}{2},\ 2,\ \tfrac{5}{2},\ \dots $$

Cette quantification permet de classer les particules en deux grandes familles bien distinctes :

Bosons : ils possèdent un spin entier. Les photons, les gluons et d'autres particules porteuses d'interactions fondamentales en font partie.
Fermions : leur spin est demi-entier. Ce sont eux qui constituent la matière, comme les électrons, les protons, les neutrons ou les neutrinos.

Le spin $ \tfrac{1}{2} $ occupe une place centrale dans la physique moderne, car c'est celui des particules qui composent les atomes. Comprendre leur comportement revient, en grande partie, à comprendre les règles qui gouvernent ce type de spin.

Lorsqu'on mesure la projection du spin d'un électron sur un axe donné, seuls deux résultats sont possibles :

projection positive : $+\tfrac{1}{2}$
projection négative : $-\tfrac{1}{2}$

Pour décrire ce comportement, les vecteurs classiques en trois dimensions ne suffisent pas. La mécanique quantique utilise alors un objet mathématique beaucoup plus adapté : le spinor.

example

Un spinor possède deux composantes et obéit à des règles de transformation très particulières, propres au groupe $ SU(2) $. C'est un outil fondamental pour expliquer pourquoi les particules de spin demi-entier se comportent d'une manière qui défie l'intuition classique.

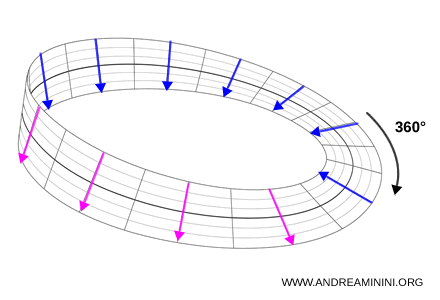
Un exemple célèbre illustre ce caractère étrange. Si l'on effectue une rotation de 360° sur un spinor, on n'obtient pas exactement l'état initial, mais un état identique à un signe près. Il faut une rotation complète de 720° pour revenir au point de départ. Ce résultat, contre-intuitif, est pourtant parfaitement confirmé par la théorie.

L'analogie avec la bande de Möbius permet de visualiser cette idée. Après un premier tour, l'orientation est inversée. Ce n'est qu'au second tour que l'on retrouve la configuration initiale.

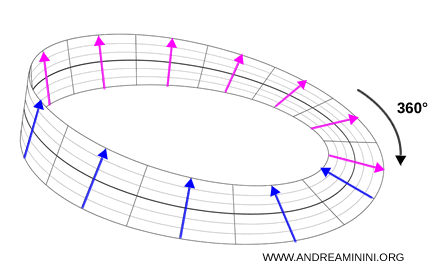
analogie Möbius montrant l'inversion d'un spinor après 360 degrés

Après deux tours, tout coïncide de nouveau.

spinor retrouvant son état initial après une rotation totale de 720 degrés

Dans le formalisme de Pauli, les particules de spin 1/2 sont décrites à l'aide d'un spinor à deux composantes :

$$ \chi = \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$

Les coefficients complexes $\alpha$ et $\beta$ contiennent toutes les informations probabilistes sur les mesures possibles du spin.

Note. Si l'on change d'axe de référence, le spinor se transforme grâce à un opérateur unitaire : $$ \begin{pmatrix} \alpha' \\ \beta' \end{pmatrix} = U(\theta) \begin{pmatrix} \alpha \\ \beta \end{pmatrix} $$ avec $$ U(\theta) = e^{- i \theta \cdot \sigma /2} $$. Les matrices $ \sigma $ sont les matrices de Pauli, au cœur de la description du spin 1/2.

Comment les différentes particules sont représentées

La représentation mathématique d'une particule dépend directement de son spin. Chaque classe possède ses propres outils.

Spin 1. Les particules comme le photon se décrivent par des vecteurs à trois composantes, qui se transforment selon le groupe $ SO(3) $.
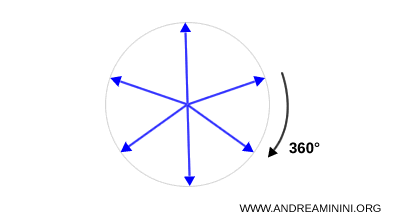
Spin $ \tfrac{1}{2} $. Les spinors relèvent du groupe $ SU(2) $, une structure mathématique étroitement liée à $ SO(3) $. C'est la raison pour laquelle ils nécessitent une rotation de 720° pour retrouver leur état initial.

Note. Les représentations $ SO(3) $ en trois dimensions et $ SU(2) $ en deux dimensions montrent clairement la différence entre les particules de spin entier et celles de spin demi-entier.
Spin $ \tfrac{3}{2} $. Ces particules nécessitent des spinors à quatre composantes, correspondant à des représentations plus riches de $ SU(2) $. Elles conservent toutes les propriétés caractéristiques des spins demi-entiers.

En résumé :

Spin 0 : représentation scalaire (1 dimension)
Spin $ \tfrac{1}{2} $ : représentation spinorielle (2 dimensions)
Spin 1 : représentation vectorielle (3 dimensions)
Spin $ \tfrac{3}{2} $ : représentation spinorielle étendue (4 dimensions)

Le spin dans la théorie quantique des champs

Au départ, le spin a été introduit dans la mécanique quantique non relativiste pour expliquer certains phénomènes expérimentaux, comme la structure fine des spectres atomiques ou l'effet Zeeman. Mais pour comprendre pleinement son origine, il faut se tourner vers le cadre relativiste.

C'est dans l'équation de Dirac que le spin apparaît naturellement. Cette équation, qui décrit le comportement relativiste de l'électron, prédit l'existence d'un spin $ \tfrac{1}{2} $ et explique un ensemble de résultats essentiels, dont le moment magnétique anormal.

Le lien entre spin et structure quantique devient particulièrement clair à travers trois idées majeures :

Le principe d'exclusion de Pauli, qui stipule que deux fermions identiques ne peuvent pas partager le même état quantique.
Les statistiques quantiques, qui distinguent les comportements des bosons et des fermions.
Les moments magnétiques des particules, étroitement liés au spin et à la structure interne des champs quantiques.

Le spin est l'exemple parfait d'une propriété qui n'a pas de contrepartie en physique classique. Il n'a de sens que dans le cadre quantique, et sa compréhension complète exige les outils de la relativité.

De la structure des atomes aux interactions fondamentales, le spin joue un rôle déterminant dans la manière dont la matière est organisée. Et malgré un siècle de recherches, il continue de nourrir de nouvelles questions.