Particules Xi

La particule Xi (prononcée « ksi », d’après la lettre grecque Ξ) est un baryon, c’est-à-dire une particule composée de trois quarks. Elle appartient à la famille des particules étranges, car elle contient deux quarks étranges (s).

On l’appelle aussi baryon cascade, car dans les détecteurs de particules elle se désintègre généralement par une suite de transformations successives, plutôt que par une seule transition directe.

Il existe deux types principaux de particules Xi :

• $ \Xi^0 $, composée des quarks (u, s, s), soit un quark up (u) et deux quarks étranges (s)
• $ \Xi^- $, composée des quarks (d, s, s), soit un quark down (d) et deux quarks étranges (s)

Dans les deux cas, la présence de deux quarks étranges constitue la caractéristique fondamentale qui distingue les particules Xi des protons et des neutrons.

Charge électrique

Les deux particules Xi possèdent les charges électriques suivantes :

• $ \Xi^0 $ possède une charge électrique nulle
• $ \Xi^- $ possède une charge électrique égale à -1

La charge électrique totale d’une particule correspond à la somme des charges électriques des quarks qui la composent.

• $ q(u) = +2/3 $
• $ q(d) = -1/3 $
• $ q(s) = -1/3 $

Spin et classification

Les particules Xi se répartissent en deux familles, de manière analogue aux baryons Sigma :

• Xi ordinaires (Ξ)
  Elles possèdent un spin \( \frac{1}{2} \) et appartiennent à l’octet baryonique. Dans cette configuration, les spins des quarks ne sont pas tous alignés (par exemple ↑↑↓), ce qui conduit à un spin total égal à un demi. $$ \tfrac 12 + \tfrac 12 - \tfrac 12 = \tfrac 12 $$
• Xi étoile (Ξ*)
  Elles possèdent un spin \( \frac{3}{2} \) et appartiennent au décuplet baryonique. Les quarks sont alors dans un état excité, avec tous les spins alignés (↑↑↑). Le spin total vaut donc trois demis. $$ \tfrac 12 + \tfrac 12 + \tfrac 12 = \frac{1+1+1}{2} = \tfrac 32 $$

Les particules Xi occupent une position bien définie dans le schéma de classification de la voie octuple.

Elles apparaissent dans les niveaux inférieurs des multiplets, car leur étrangeté vaut -2.

Isospin des particules Xi

Les particules Xi (Ξ) forment un doublet d’isospin, car elles contiennent deux quarks étranges (s), tandis que le troisième quark est soit un quark up (u), soit un quark down (d).

Comme seuls les quarks up et down contribuent à l’isospin, et que le quark étrange possède un isospin nul, un seul quark apporte une contribution égale à $ \frac 12 $.

L’isospin total des particules Xi vaut donc :

$$ I = \tfrac{1}{2} $$

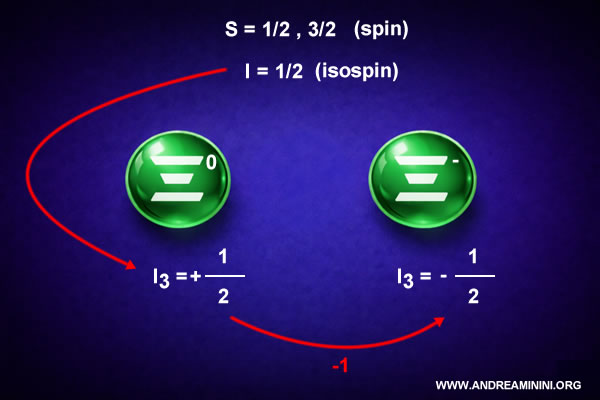
La troisième composante de l’isospin, notée $ I_3 $, peut prendre deux valeurs :

• \( I_3 = +\tfrac{1}{2} \)
• \( I_3 = -\tfrac{1}{2} \)

Il en résulte deux états distincts :

• $ \Xi^0 $ (uss) avec un isospin $ I_3 = \tfrac12 $
• $ \Xi^- $ (dss) avec un isospin $ I_3 = -\tfrac12 $

Pour cette raison, les particules Xi forment un doublet, étroitement analogue au système proton - neutron.

Note. À titre de vérification, le nombre d’états quantiques associés à un multiplet de particules est donné par la relation $$ 2I + 1 $$ Dans le cas des particules Xi, on observe deux états distincts, ce qui implique $$ 2I + 1 = 2 $$ On en déduit donc directement $$ I = \frac{2-1}{2} = \tfrac12 $$ Cela confirme que les particules Xi forment un doublet d’isospin.

Désintégration

Les particules Xi se désintègrent par interaction faible, par exemple :

$$ \Xi^- \to \Lambda^0 + \pi^- $$

Cette désintégration est lente par rapport aux interactions fortes, car elle implique une variation de l’étrangeté.

Et ainsi de suite.