Électrodynamique quantique

Électrodynamique quantique (QED, pour son acronyme anglais) est la théorie quantique des champs qui décrit comment les particules chargées (telles que les électrons, les positrons et les quarks) interagissent entre elles par l’échange de photons.

Elle est considérée comme la plus ancienne, la plus simple et, en même temps, la plus précise et la plus féconde de toutes les théories quantiques des champs.

La QED s’est développée comme une extension de la théorie classique de l’électromagnétisme de Maxwell, adaptée à la mécanique quantique et à la relativité restreinte. Elle a également fourni les bases de théories ultérieures essentielles, comme la chromodynamique quantique et la théorie électrofaible.

Elle a été formulée et perfectionnée dans les années 1940 par Tomonaga, Feynman et Schwinger.

Pourquoi est-elle capitale ? La QED atteint une précision inégalée : ses prédictions coïncident avec les mesures expérimentales jusqu’à la douzième décimale. Elle a en outre introduit des outils centraux de la physique moderne, tels que les diagrammes de Feynman et la notion de particules virtuelles. Plus largement, elle s’est imposée comme le modèle de référence de toutes les théories de jauge, y compris du Modèle standard.

En résumé, comment fonctionne-t-elle ?

La QED interprète toute interaction électromagnétique comme un échange de photons entre particules chargées.

Autrement dit, les particules chargées n’agissent jamais directement les unes sur les autres.

L’interaction résulte de l’échange de photons virtuels, représentés par des lignes internes dans les diagrammes de Feynman.

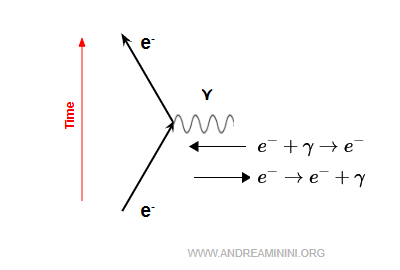
Un électron peut :

• émettre un photon virtuel  $$ e^- \;\rightarrow\; e^- + \gamma $$
• absorber un photon virtuel  $$ e^- + \gamma \;\rightarrow\; e^- $$

Remarque. Les photons réels sont des particules observables (comme la lumière visible). Les photons virtuels, eux, ne sont pas des particules libres : on ne peut pas les détecter directement, ils ne jouent que le rôle d’intermédiaires transmettant l’interaction.

En physique classique, deux électrons se repoussent parce qu’ils portent la même charge électrique (répulsion de Coulomb).

En QED, cette répulsion s’explique comme un échange permanent de photons virtuels entre les deux électrons.

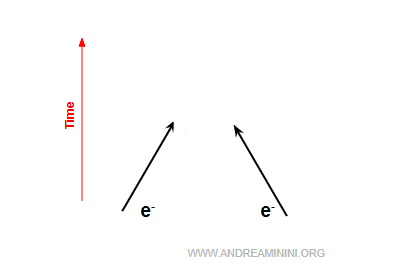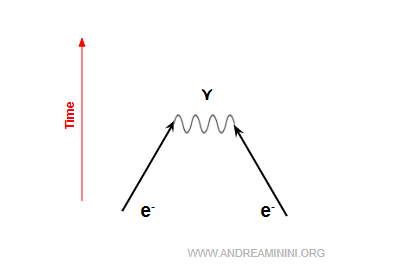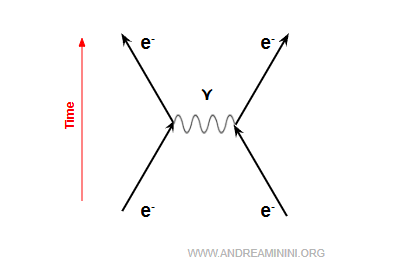
Ces photons virtuels transportent de la quantité de mouvement, et leur échange dévie les trajectoires des électrons, les contraignant à s’éloigner.

Ce processus est connu en QED sous le nom de diffusion de Møller, puisqu’il met en jeu deux électrons.

$$ e^- + e^- \rightarrow e^- + e^- $$

Ainsi, chaque fois que deux particules chargées « s’influencent » à distance, il ne s’agit pas d’une action instantanée (comme en physique classique), mais du résultat d’un échange quantique de photons virtuels.

Remarque. Si deux particules portent des charges de même signe, l’échange de photons virtuels engendre une répulsion. Si leurs charges sont opposées, l’échange produit une attraction. Les photons virtuels sont donc les vecteurs de l’interaction électromagnétique, capables de transmettre aussi bien la répulsion que l’attraction, selon la nature de la charge. Il importe de le souligner, car on croit souvent, à tort, qu’ils « ne transmettent que la répulsion ».

Exemples

Voici quelques-uns des processus les plus représentatifs décrits par la QED :

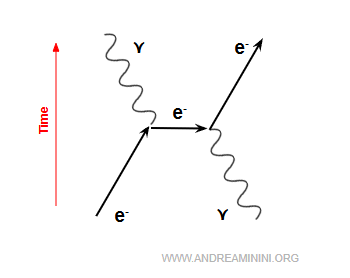
1] Diffusion Compton

Un électron entre en collision avec un photon réel et le diffuse.

$$ e^- + \gamma \;\longrightarrow\; e^- + \gamma $$

Dans ce processus, un photon heurte un électron et ressort avec une longueur d’onde modifiée (effet Compton).

Ce fut l’une des preuves les plus convaincantes du caractère corpusculaire de la lumière.

Voici sa représentation dans un diagramme de Feynman, où l’axe du temps est dirigé vers le haut.

2] Annihilation

Dans ce processus, un électron ($e^-$) et un positron ($e^+$, son antiparticule) se rencontrent et transforment leur masse en énergie sous forme de photons.

$$ e^- + e^+ \;\;\longrightarrow\;\; \gamma + \gamma $$

La conservation de l’énergie et de la quantité de mouvement impose la création d’au moins deux photons dans l’état final, émis dans des directions opposées.

Comme les photons sont leurs propres antiparticules, la production de deux garantit le respect de toutes les lois de conservation.

Voici comment l’annihilation électron-positron apparaît dans un diagramme de Feynman.

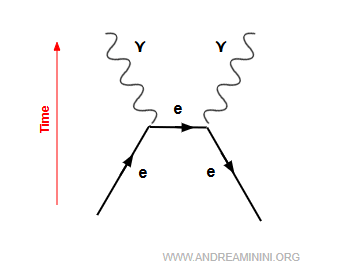
La flèche orientée à rebours du temps représente l’antiparticule de l’électron : le positron.

En essence, l’annihilation électron-positron est le processus inverse de la création de paires ($\gamma + \gamma \to e^- + e^+$).

3] Création de paires

C’est le processus inverse de l’annihilation : un photon de haute énergie se convertit en une paire particule-antiparticule, généralement un électron et un positron :

$$ \gamma + \gamma  \;\;\longrightarrow\;\; e^- + e^+ $$

Deux photons se transforment en une paire électron-positron.

Autrement dit, la création de paires est la conversion d’énergie lumineuse en matière (une particule et son antiparticule).

 

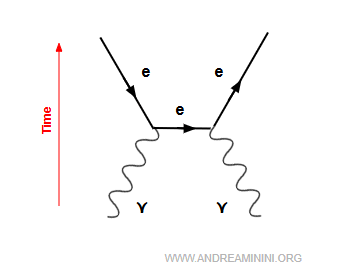
C’est l’inverse de l’annihilation et une illustration frappante de l’équivalence masse-énergie, $E = mc^2$.

Remarque. Ce processus ne peut pas se produire dans le vide : un seul photon ne peut se transformer en une paire, car cela violerait la conservation de la quantité de mouvement. La présence d’un noyau voisin (ou plus rarement d’un autre électron) est nécessaire pour jouer le rôle de « cible » et absorber une partie de l’impulsion. Le processus réel est donc : $$ \gamma + N \;\; \longrightarrow\;\; e^- + e^+ + N $$ où $N$ est le noyau, qui reste pratiquement inchangé. Par exemple, un photon gamma incident sur un atome lourd peut engendrer une paire $e^- + e^+$.

4] Diffusion Bhabha

Il s’agit de la diffusion élastique entre un électron et un positron.

$$ e^- + e^+ \;\;\longrightarrow\;\; e^- + e^+ $$

Elle doit son nom au physicien indien Homi Jehangir Bhabha, qui fut, en 1935, le premier à calculer sa section efficace dans le cadre de la QED.

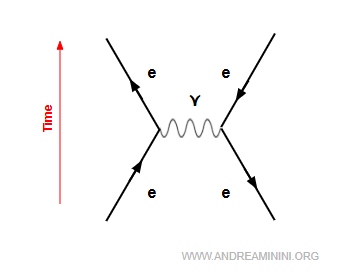
Un électron et un positron s’annihilent en un photon virtuel.

$$ e^+ + e^- \rightarrow \gamma + \gamma $$

Presque aussitôt, ce photon engendre une nouvelle paire électron-positron $e^- + e^+$.

$$ \gamma + \gamma \rightarrow e^+ + e^- $$

En d’autres termes, un électron et un positron entrent, un électron et un positron ressortent. Ce ne sont pas les mêmes, évidemment, mais comme les électrons sont par nature indiscernables, cela ne change rien sur le plan physique.

Remarque. Un photon représenté comme une ligne interne dans un diagramme de Feynman est une particule virtuelle, non soumise à la relation de dispersion usuelle $ E = pc $. Il peut transporter une énergie et une impulsion arbitraires, ce qui le place « hors de la couche de masse » (off-shell). C’est pourquoi un diagramme peut légitimement montrer un seul photon virtuel sans violer les lois de conservation au niveau de ce sommet. En revanche, dans le processus physique, toute annihilation électron-positron doit produire deux photons réels afin de préserver simultanément l’énergie et la quantité de mouvement. Les lignes externes du diagramme représentent ces particules réelles, comme dans la diffusion Bhabha, où l’état final est à nouveau une paire électron-positron.

Quelle est la différence entre photons réels et virtuels ?

En QED, il est crucial d’opérer une distinction nette entre photons réels et photons virtuels.

• Photons réels
  Un photon réel est un quantum observable du champ électromagnétique. Il se propage librement dans l’espace à la vitesse de la lumière et satisfait strictement la relation énergie-impulsion ; autrement dit, il est « sur la couche de masse » (on-shell) : $$ E^2 = (pc)^2 + (mc^2)^2 \quad \;\; \text{avec } m=0 \;\Rightarrow\; E = pc $$ Les photons réels sont ceux que nous pouvons détecter directement : lumière visible, rayons X ou rayonnement gamma.

  Exemples : la lumière solaire qui atteint la Terre, le faisceau cohérent d’un laser ou un photon gamma émis lors d’une désintégration nucléaire. En pratique, les photons réels constituent le rayonnement électromagnétique mesurable avec nos instruments.

• Photons virtuels
  Les photons virtuels, eux, sont les « médiateurs cachés » des interactions électromagnétiques. Leur échange est à l’origine des forces, qu’il s’agisse de l’attraction ou de la répulsion de Coulomb entre charges. Mais un photon virtuel n’est pas une particule détectable : il n’apparaît que comme ligne interne dans les diagrammes de Feynman, représentant des états intermédiaires de l’interaction. Contrairement aux photons réels, il n’est pas soumis à la relation $E = pc$. Il peut transporter des combinaisons d’énergie et de quantité de mouvement impossibles pour un photon libre, ce qui explique qu’il soit dit « hors de la couche de masse » (off-shell). En ce sens, le terme « photon virtuel » relève davantage d’une construction conceptuelle propre au formalisme de Feynman que de la description d’une particule physique au sens habituel.

  Remarque. On entend souvent dire que les photons virtuels « n’existent qu’un instant » en vertu du principe d’incertitude de Heisenberg : $$ \Delta E \, \Delta t \gtrsim \hbar $$ L’idée est qu’un système peut « emprunter » une énergie $\Delta E$ à condition de la « rendre » dans un laps de temps suffisamment court $\Delta t$. Plus la violation énergétique est grande, plus l’intervalle permis est bref. Cette image, bien qu’heuristique et utile pour l’intuition, ne reflète pas la rigueur de la QED : les photons virtuels n’ont pas d’existence autonome, ce ne sont que des termes mathématiques issus du développement perturbatif. L’énergie et la quantité de mouvement se conservent exactement à chaque sommet d’interaction ; ce qui n’est pas exigé entre sommets, c’est la condition d’être un photon libre et on-shell.

Écran quantique en QED

En électrodynamique quantique, le vide n’est pas un espace inerte, mais un fond en perpétuelle agitation de fluctuations quantiques. Durant des intervalles infinitésimaux, ces fluctuations peuvent donner naissance à des paires virtuelles électron-positron, représentées dans les diagrammes de Feynman comme une boucle de fermions reliée à une ligne de photon virtuel. 

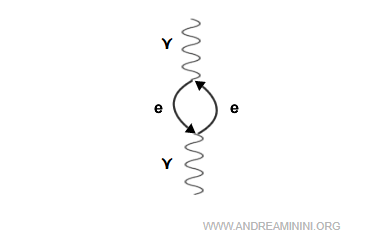
De ce fait, le vide se comporte de manière analogue à un milieu diélectrique. Ce phénomène est appelé polarisation du vide.

Une charge électrique réelle (par exemple un électron) interagit en permanence avec ces paires virtuelles.

Les positrons virtuels (charges positives) sont attirés vers la charge négative de l’électron, tandis que les électrons virtuels (charges négatives) sont repoussés.

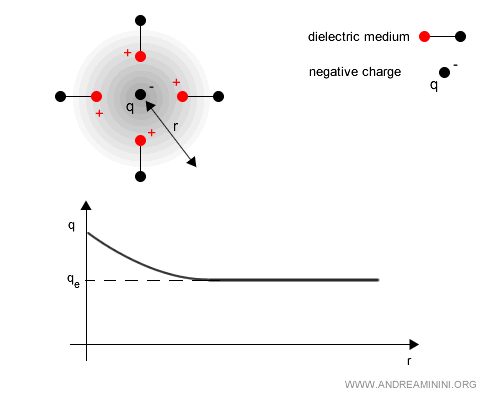
Il en résulte un « nuage » de charge opposée autour de la particule, qui atténue l’intensité du champ électrique externe.

À grande distance, la charge effective $ q_e $ apparaît donc plus faible que la charge nue $ q $.

Ce phénomène est connu sous le nom d’écran du vide.

À très courte distance - ou, de manière équivalente, à haute énergie - on pénètre la « nuée » de polarisation et l’on mesure une charge effective plus forte.

C’est pourquoi la constante de couplage électron-photon $ \alpha $ n’est pas une grandeur fixe, mais dépend de l’échelle d’énergie : un effet appelé variation (running) de la constante de couplage.

Remarque. Le même mécanisme agit avec des charges positives : les électrons virtuels se concentrent autour de la charge, tandis que les positrons virtuels sont repoussés. Le résultat est toujours la polarisation du vide. 

 

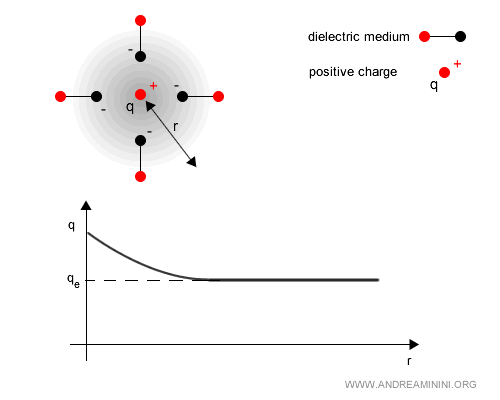
La charge nue étant en permanence « masquée » par cet écran, elle ne peut être mise en évidence qu’à des distances extrêmement courtes. 

La charge que nous mesurons expérimentalement est donc la charge « effective », autrement dit la charge habillée par le vide.

Et ainsi de suite.