Moment angulaire des particules
En mécanique quantique, le moment angulaire d'une particule décrit comment son état réagit aux rotations dans l'espace. Il s'agit d'un outil fondamental pour comprendre les symétries de la fonction d'onde et la dynamique interne des systèmes quantiques.
Ce concept joue un rôle central dans l'étude des électrons dans les atomes, dans l'analyse des spectres et dans l'explication de nombreuses propriétés magnétiques. On distingue deux formes complémentaires de moment angulaire, qui se manifestent dans tous les systèmes quantiques :
- Moment angulaire orbital \( L \)
Il reflète l'organisation spatiale de la fonction d'onde. Il ne correspond pas à une orbite matérielle, mais à la symétrie de la distribution de probabilité. Sa quantification indique comment l'état de la particule s'ordonne dans l'espace tridimensionnel. - Moment angulaire intrinsèque (spin) \( S \)
Il s'agit d'une propriété interne et purement quantique. Contrairement au moment orbital, le spin n'est lié à aucun mouvement réel dans l'espace. Il est décrit par les transformations SU(2) et n'a pas d'équivalent classique.
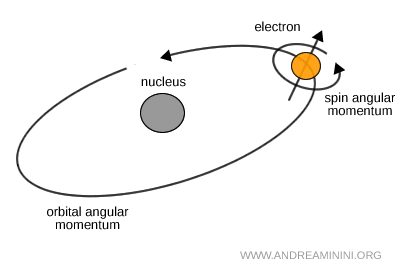
Note. Le spin est souvent représenté comme une rotation sur soi-même, mais cette image est trompeuse. Il s'agit d'une propriété intrinsèque qui ne correspond à aucune rotation physique réelle. Pourtant, ses effets sont bien observables, notamment dans les phénomènes magnétiques ou le dédoublement de certains niveaux d'énergie. Le moment orbital \( L \), en revanche, est directement lié à la géométrie de l'espace.
Un concept classique qui change de nature en mécanique quantique
En mécanique classique, le moment angulaire s'écrit \( \vec{L} = \vec{r} \times m\vec{v} \), ce qui permet de le décomposer en trois composantes sur les axes cartésiens :
$$ \vec{L} = (L_x,\,L_y,\,L_z) $$
Chacune de ces composantes représente la projection du moment angulaire sur un axe de l'espace.
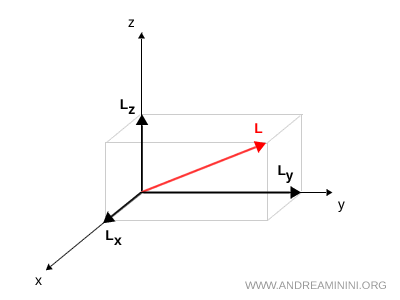
La mécanique quantique modifie radicalement cette image. Il est impossible de mesurer simultanément les trois composantes \( L_x \), \( L_y \) et \( L_z \). La mesure d'une composante perturbe les autres, ce qui limite l'accès à l'information. En pratique, on mesure une seule projection, par convention celle associée à l'axe \( z \). L'observable pertinente devient donc \( L_z \).
On peut également déterminer la valeur du module du moment angulaire :
$$ L = \sqrt{l(l+1)}\,\hbar $$
Le nombre quantique \( l \) prend des valeurs entières positives ou nulles. La constante \( \hbar \), appelée constante de Planck réduite, définit l'échelle des effets quantiques et intervient dans toutes les lois fondamentales de la théorie.
Note. La constante \( \hbar \) est définie par $$ \hbar = \frac{h}{2\pi} $$ où \( h \) est la constante de Planck. Sa valeur approchée est $$ \hbar \approx 1.054 \times 10^{-34} , \text{J⋅s} $$. On la retrouve dans l'équation de Schrödinger, dans le principe d'incertitude et dans toutes les lois de la mécanique quantique.
Une grandeur quantifiée
L'expression \( L = \sqrt{l(l+1)}\,\hbar \) montre que le moment angulaire ne varie pas continûment. Il ne peut prendre que certaines valeurs discrètes fixées par le nombre quantique \( l \). Le tableau suivant illustre les premiers cas possibles :
| \(l\) | \(|\vec{L}|=\sqrt{l(l+1)}\,\hbar\) | Valeur |
|---|---|---|
| 0 | \(\sqrt{0\cdot 1}\,\hbar\) | \(0\) |
| 1 | \(\sqrt{1\cdot 2}\,\hbar\) | \(\sqrt{2}\,\hbar\) |
| 2 | \(\sqrt{2\cdot 3}\,\hbar\) | \(\sqrt{6}\,\hbar\) |
| 3 | \(\sqrt{3\cdot 4}\,\hbar\) | \(\sqrt{12}\,\hbar\) |
| 4 | \(\sqrt{4\cdot 5}\,\hbar\) | \(\sqrt{20}\,\hbar\) |
| 5 | \(\sqrt{5\cdot 6}\,\hbar\) | \(\sqrt{30}\,\hbar\) |
Pour simplifier les calculs, on utilise fréquemment le carré du module, noté \( L^2 \) :
$$ L^2 = l(l+1)\hbar^2 $$
| \(l\) | \(L^2 = l(l+1)\hbar^2\) | Valeur |
|---|---|---|
| 0 | \(0\cdot 1\,\hbar^2\) | \(0\,\hbar^2\) |
| 1 | \(1\cdot 2\,\hbar^2\) | \(2\,\hbar^2\) |
| 2 | \(2\cdot 3\,\hbar^2\) | \(6\,\hbar^2\) |
| 3 | \(3\cdot 4\,\hbar^2\) | \(12\,\hbar^2\) |
| 4 | \(4\cdot 5\,\hbar^2\) | \(20\,\hbar^2\) |
| 5 | \(5\cdot 6\,\hbar^2\) | \(30\,\hbar^2\) |
En mécanique quantique, l’opérateur \( \hat{L}^2 \) possède des valeurs propres parfaitement définies. C’est pourquoi, dans de nombreux contextes, il est souvent plus simple et plus efficace de travailler avec \( L^2 \) plutôt qu’avec le module \( |\vec{L}| \), en particulier lorsqu’on étudie des états stationnaires.
Note. Cette quantification est une propriété exclusivement quantique. En physique classique, le module du moment angulaire peut varier continûment et prendre n’importe quelle valeur réelle.
La projection du moment angulaire orbital sur l’axe \( z \) est elle aussi quantifiée et s’exprime par la relation fondamentale :
$$ L_z = m_l \hbar $$
Le paramètre \( m_l \), appelé nombre quantique magnétique, ne peut prendre que des valeurs entières comprises entre \( -l \) et \( l \) :
$$ m_l = -l, -l+1, \dots, -1, 0, +1, \dots, l-1, l $$
Le tableau ci-dessous rassemble les valeurs permises de \( m_l \), les projections correspondantes \( L_z \) et le nombre total d’états associés à chaque valeur de \( l \).
| \(l\) | Valeurs permises de \(m_l\) | Valeurs correspondantes de \(L_z\) | Nombre d’états \((2l+1)\) |
|---|---|---|---|
| 0 | \(0\) | \(0\) | 1 |
| 1 | \(-1,\,0,\,+1\) | \(-\hbar,\,0,\,+\hbar\) | 3 |
| 2 | \(-2,\,-1,\,0,\,+1,\,+2\) | \(-2\hbar,\,-\hbar,\,0,\,+\hbar,\,+2\hbar\) | 5 |
| 3 | \(-3,\,-2,\,-1,\,0,\,+1,\,+2,\,+3\) | \(-3\hbar,\,-2\hbar,\,-\hbar,\,0,\,+\hbar,\,+2\hbar,\,+3\hbar\) | 7 |
Par exemple, si \( l = 2 \), la projection de \( \vec{L} \) sur l’axe \( z \) ne peut prendre que cinq valeurs distinctes : \(-2\hbar, -\hbar, 0, +\hbar, +2\hbar\).
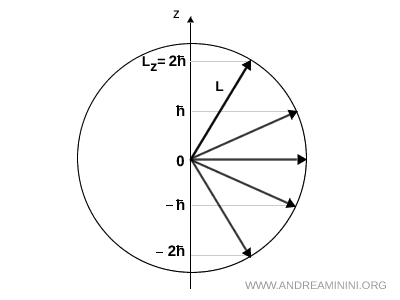
Dans ce cas, le module du moment angulaire vaut \( |\vec{L}| = \sqrt{l(l+1)}\,\hbar \). Tous les vecteurs ont donc la même longueur et se répartissent sur la surface d’une sphère. Seule la projection \( L_z \) adopte des valeurs discrètes de la forme \( L_z = m_l \hbar \).
Les cinq flèches représentées illustrent clairement les orientations possibles de \( \vec{L} \) lorsque \( l = 2 \). Leur module est identique, mais leur angle par rapport à l’axe \( z \) diffère, exactement comme l’impose la condition \( L_z = m_l \hbar \).
Note. Même lorsque \( m_l = l \), le vecteur \( \vec{L} \) ne peut jamais s’aligner parfaitement sur l’axe \( z \). S’il y parvenait, on aurait \( |\vec{L}| = |L_z| \), alors qu’en réalité \( |\vec{L}| = \sqrt{l(l+1)}\,\hbar \), valeur toujours supérieure à \( l\hbar \). Il subsiste donc nécessairement des composantes sur les autres axes, ce qui entraîne le mouvement de précession.
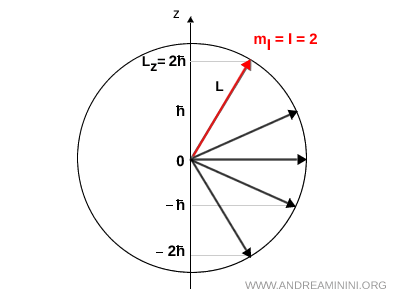
Il est essentiel de garder à l’esprit que \( L_z \) est une composante vectorielle orientée. Elle peut être positive, négative ou nulle. Le module, en revanche, est toujours positif. Cette distinction est cruciale pour interpréter correctement la signification physique de \( L_z \).
Moment angulaire de spin
Le spin est le moment angulaire intrinsèque d'une particule. C'est l'une des caractéristiques fondamentales de la matière à l'échelle quantique et elle joue un rôle essentiel dans la structure des atomes, l'origine du magnétisme et la physique des particules en général.
Contrairement au moment angulaire orbital, le spin ne provient d'aucun mouvement réel dans l'espace. Il s'agit d'une propriété interne, aussi fondamentale que la masse ou la charge électrique. Pourtant, sur le plan mathématique, il obéit aux mêmes relations que tout moment angulaire quantique. C'est l'une des raisons pour lesquelles le spin occupe une place centrale dans la théorie quantique.
Le module du vecteur spin est quantifié et s'exprime sous la forme
$$ S = \sqrt{ s(s+1) } \hbar $$
ou, de façon équivalente, à travers son carré
$$ S^2 = s(s+1) \hbar^2 $$
Le nombre quantique de spin \( s \) peut prendre des valeurs entières ou demi-entières :
$$ s = 0, \tfrac12, 1, \tfrac32, 2, \tfrac52, \ldots $$
La projection du spin sur un axe choisi, généralement l'axe \( z \), est également quantifiée :
$$ S_z = m_s \hbar $$
Le nombre quantique magnétique \( m_s \) peut prendre les valeurs \( m_s = -s, -s+1, \ldots, s-1, s \), ce qui donne au total \( 2s+1 \) états possibles.
Pour l'électron, où \( s = \tfrac12 \), il existe deux états distincts : \( m_s = +\tfrac12 \), appelé état spin up, et \( m_s = -\tfrac12 \), appelé état spin down.
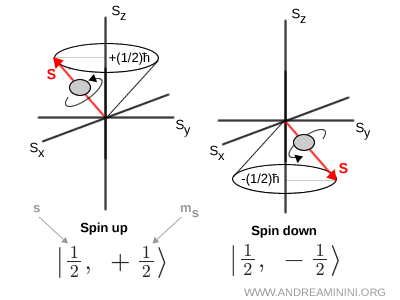
Dans le formalisme de la mécanique quantique, ces états se notent à l'aide de la notation bra-ket : \( | s,\ m_s \rangle \). Par exemple, \( \left| \tfrac12,\ +\tfrac12 \right\rangle \) désigne l'état spin up et \( \left| \tfrac12,\ -\tfrac12 \right\rangle \) l'état spin down.
Note. Le spin ne provient d'aucune rotation physique dans l'espace. En revanche, comme le moment angulaire orbital, il possède une valeur totale quantifiée et une seule composante mesurable le long d'un axe de référence.
Valeurs typiques du spin
Le tableau suivant présente quelques valeurs de \( s \), les projections possibles \( m_s \) et les valeurs associées de \( S_z \). Cette structure discrète des états est l'une des signatures les plus caractéristiques du monde quantique.
| \( s \) | \( S^2 = s(s+1)\hbar^2 \) | Valeurs de \( m_s \) | Valeurs de \( S_z \) | États possibles \( 2s+1 \) |
|---|---|---|---|---|
| \( \tfrac12 \) | \( \tfrac34 \hbar^2 \) | \( -\tfrac12, +\tfrac12 \) | \( -\tfrac12\hbar, +\tfrac12\hbar \) | 2 |
| \( 1 \) | \( 2\hbar^2 \) | \( -1, 0, +1 \) | \( -\hbar, 0, +\hbar \) | 3 |
| \( \tfrac32 \) | \( \tfrac{15}{4}\hbar^2 \) | \( -\tfrac32, -\tfrac12, +\tfrac12, +\tfrac32 \) | \( -\tfrac32\hbar, -\tfrac12\hbar, +\tfrac12\hbar, +\tfrac32\hbar \) | 4 |
Une propriété vraiment intrinsèque
Le spin est une caractéristique immuable de la particule. Une particule peut changer d'état orbital, mais sa valeur de \( s \) ne varie pas. Par exemple, le proton, le neutron et l'électron possèdent toujours \( s = \tfrac12 \), tandis que le photon et le gluon ont \( s = 1 \).
| Bosons (spin entier) | Fermions (spin demi-entier) | ||
|---|---|---|---|
| Spin 0 | Spin 1 | Spin \( \tfrac{1}{2} \) | Spin \( \tfrac{3}{2} \) |
| Mésons pseudo-scalaires $ \pi, K, \eta, \eta' $ |
Photons ( \( \gamma \) ) Gluons ( \( g \) ) Bosons \( W^+, W^-, Z \) Mésons vectoriels $ \rho, \omega, \phi, K^*, J/\psi, \Upsilon $ |
Quarks, leptons protons ( \( p \) ), neutrons ( \( n \) ) électrons ( \( e \) ) Octet baryonique $ p,\ n , \Sigma^{+},\ \Sigma^{0},\ \Sigma^{-} $ $ \Xi^{0},\ \Xi^{-} , \Lambda^{0} $ |
Déculpette baryonique $ \Delta^{++},\ \Delta^{+},\ \Delta^{0},\ \Delta^{-} $ $ \Sigma^{*+},\ \Sigma^{*0},\ \Sigma^{*-} $ $ \Xi^{*0},\ \Xi^{*-} $ $ \Omega^{-} $ |
En résumé, les particules de spin entier sont appelées bosons et obéissent à la statistique de Bose-Einstein, tandis que celles de spin demi-entier sont appelées fermions et vérifient le principe d'exclusion de Pauli.
Note avancée. Dans le cas des fermions, un auto-état de spin ne retrouve exactement sa configuration initiale qu'après une rotation de \( 4\pi \). Ce comportement, sans équivalent classique, met clairement en évidence la nature profondément quantique du spin.
Un exemple concret
Considérons maintenant un électron dans un orbital (p), caractérisé par le nombre quantique
$$ l = 1 $$
Dans une orbitale de type (p), deux contributions indépendantes interviennent dans le moment angulaire total :
- \( L \), qui décrit la symétrie spatiale de la fonction d’onde et détermine la géométrie de l’orbitale
- \( S \), qui définit l’état de spin et n’influence pas la forme spatiale
Observons d’abord la contribution orbitale.
1) Moment angulaire orbital \( \mathbf{L} \)
Pour \( l = 1 \), on obtient :
$$ L^2 = l(l+1)\hbar^2 = 2\hbar^2 $$
$$ |\mathbf{L}| = \sqrt{2}\,\hbar $$
où \( \hbar \) représente la constante de Planck réduite.
Les orbitales (p), reconnaissables à leur forme en deux lobes, sont décrites par les harmoniques sphériques
$$ Y_1^{-1},\; Y_1^{0},\; Y_1^{+1} $$
associées aux valeurs permises
$$ m_l = -1,\; 0,\; +1 $$
Dans l’espace, \( \mathbf{L} \) ne pointe pas dans une direction fixe : il précesse en décrivant un cône autour de l’axe \( z \).
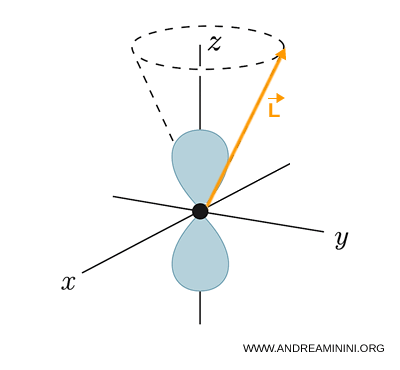
La géométrie caractéristique des orbitales (p) est l’exacte manifestation du fait que \( l = 1 \).
2) Moment angulaire de spin \( \mathbf{S} \)
L’électron possède également un spin :
$$ s = \frac{1}{2} $$
avec deux valeurs possibles
$$ m_s = \pm \frac{1}{2} $$
Chaque orbitale (p) peut donc exister sous deux états de spin :
- (p) avec \( m_s = +\tfrac{1}{2} \)
- (p) avec \( m_s = -\tfrac{1}{2} \)
Le spin n’est pas lié à une rotation physique de l’électron. Il s’agit d’une propriété interne, indépendante de la géométrie orbitale.
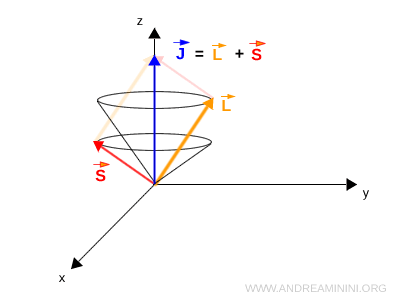
Dans un état quantique complet, le moment orbital \( L \) et le spin \( S \) s’additionnent pour former le moment angulaire total :
$$ \mathbf{J} = \mathbf{L} + \mathbf{S} $$
Ce couplage engendre les dédoublements caractéristiques observés dans les niveaux d’énergie, visibles dans les spectres atomiques sous la forme de structure fine.
Que représentent les cônes du diagramme ? Les vecteurs \( L \), \( S \) et \( J \) sont animés d’un mouvement de précession. Les deux premiers précessent autour du troisième, tandis que \( J \) précesse à son tour autour de la direction fixée par un champ magnétique externe. Cette dynamique explique les surfaces coniques visibles sur le schéma.
Combiner les moments angulaires en mécanique quantique
En physique classique, additionner deux moments angulaires ne pose aucun problème. On additionne simplement leurs composantes, et tout est fixé. En mécanique quantique, la situation change complètement. Les composantes de l'opérateur de moment angulaire ne commutent pas, ce qui interdit de connaître les trois composantes à la fois.
C'est à partir de là qu'apparaît la question essentielle. Comment combiner deux moments angulaires lorsque leurs composantes individuelles ne peuvent pas être déterminées simultanément?
Pour un moment angulaire quantique, seules deux quantités sont parfaitement bien définies:
- la projection sur l'axe z, donnée par la valeur propre \( m \) de \( J_z \)
- le moment angulaire total, caractérisé par le nombre quantique \( j \) associé à \( J^2 \)
Autrement dit, l'idée classique d'un vecteur orienté dans l'espace ne fonctionne plus. Il est donc impossible d'appliquer directement la règle d'addition vectorielle apprise en mécanique classique.
Une propriété demeure toutefois valable: les projections sur l'axe z s'additionnent simplement:
$$ m = m_1 + m_2 $$
La difficulté se situe ailleurs. La valeur du moment angulaire total n'est pas déterminée d'avance, car l'orientation relative des deux moments n'est pas un observable en mécanique quantique. Ils peuvent sembler plus ou moins alignés, mais cet alignement n'a pas de réalité physique mesurable.
Le moment angulaire total peut donc prendre plusieurs valeurs possibles, comprises entre une borne inférieure et une borne supérieure:
$$ j = \lvert j_1 - j_2 \rvert,\ \lvert j_1 - j_2 \rvert + 1,\ \ldots,\ \lvert j_1 + j_2 \rvert - 1,\ (j_1 + j_2) $$
Si les deux moments angulaires agissaient comme s'ils étaient parfaitement parallèles, on obtiendrait \( j_1 + j_2 \). S'ils se comportaient comme s'ils étaient opposés, on obtiendrait \( |j_1 - j_2| \). Toutes les configurations intermédiaires correspondent à des valeurs quantifiées régulièrement espacées.
$$ j = \lvert j_1 - j_2 \rvert,\ \underbrace{\lvert j_1 - j_2 \rvert + 1,\ \ldots,\ \lvert j_1 + j_2 \rvert - 1}_{valeurs\ quantifiées},\ (j_1 + j_2) $$
Cette structure discrète reflète la quantification des valeurs propres de \( J^2 \). Le moment angulaire total ne peut prendre que des valeurs entières ou demi-entières, comme \( j = 0, \frac{1}{2}, 1, \frac{3}{2}, 2, ... \).
Exemple. Prenons une particule de spin 1 dans un état orbital décrit par un moment angulaire \( l = 3 \). Nous devons combiner:
- le moment angulaire orbital \( j_1 = 3 \)
- le moment angulaire de spin \( j_2 = 1 \)
Si les deux moments agissaient comme s'ils étaient alignés, on obtiendrait \( j_1 + j_2 = 4 \). S'ils agissaient comme s'ils étaient opposés, on obtiendrait \( |j_1 - j_2| = 2 \). Les valeurs permises s'étendent donc de 2 à 4. Comme seules des valeurs discrètes sont possibles, le moment angulaire total peut prendre trois valeurs: $$ j = 2, 3, 4 $$ Chaque valeur correspond à une manière différente de combiner les deux moments, et donc à un état physique distinct avec son propre niveau d'énergie.
En résumé, additionner deux moments angulaires quantiques ne conduit jamais à une valeur unique. Le résultat est un ensemble discret de valeurs possibles. Les projections sur l'axe z s'additionnent de façon classique, mais le moment angulaire total ne peut occuper que certaines valeurs quantifiées situées entre deux bornes.