La symétrie SU(3) et la Eightfold Way des baryons

De nombreux baryons présentent des propriétés physiques très proches. Cette observation conduit naturellement à l'idée qu'ils peuvent être décrits à l'aide d'une symétrie plus générale que l'isospin pris isolément. Cette symétrie est SU(3), au sein de laquelle huit baryons de spin \( \tfrac12 \) s'organisent en un octet. Ce schéma de classification est connu sous le nom de Eightfold Way.

La notion de symétrie repose sur un principe simple. Les lois qui gouvernent l'interaction forte restent invariantes lorsqu'on échange des baryons possédant les mêmes nombres quantiques. Ces particules ne se distinguent alors que par leur position au sein de la multiplet.

Autrement dit, du point de vue de l'interaction forte, ces baryons sont équivalents. On peut les transformer les uns en les autres sans modifier la physique fondamentale du système.

Cette invariance est formalisée de manière rigoureuse par le groupe SU(3), qui regroupe les huit baryons de spin \( \tfrac12 \) dans une unique représentation irréductible, appelée Eightfold Way.

Note. La Eightfold Way a été proposée en 1961 par le physicien théoricien américain Murray Gell-Mann comme une classification systématique des hadrons en multiplets gouvernés par la symétrie SU(3). À l'époque, il s'agissait d'un cadre strictement phénoménologique, fondé sur des régularités expérimentales, sans interprétation microscopique. Ce n'est qu'avec l'introduction du modèle des quarks en 1964, également due à Gell-Mann, que cette classification a acquis une base physique solide, liée à la structure interne des hadrons.

Origine de la symétrie

Dans les années 1950, le nombre de baryons découverts a rapidement dépassé les attentes initiales.

Une analyse attentive a mis en évidence un fait marquant. Huit de ces particules partageaient des propriétés remarquablement similaires :

• proton \( p \)
• neutron \( n \)
• \( \Lambda \)
• \( \Sigma^+ , \Sigma^0 , \Sigma^- \)
• \( \Xi^0 , \Xi^- \)

Toutes possèdent un spin \( \tfrac12 \), participent à l'interaction forte et ont des masses du même ordre de grandeur, comprises approximativement entre 940 et 1320 MeV/(c²).

Ce faisceau d'indices montre clairement qu'il ne s'agit pas de particules indépendantes, mais des membres d'une même famille baryonique.

Une situation conceptuellement comparable s'était déjà présentée dans les années 1930 avec le proton et le neutron, que l'on a compris par la suite comme étant reliés par une symétrie SU(2). Le nouveau schéma reprenait cette idée, mais à une échelle plus large.

Note. Le proton et le neutron ont des masses presque identiques et se distinguent principalement par leur charge électrique. Werner Heisenberg a proposé de les interpréter comme deux états d'une seule et même particule, le nucléon. Pour formaliser cette idée, il a introduit le concept d'isospin, associé au groupe de symétrie SU(2).

Avec la découverte de nouveaux baryons, la question s'est imposée naturellement. Existait-il un groupe de symétrie plus large que SU(2), capable de décrire simultanément ces huit particules ? Cette question est devenue connue sous le nom de problème des huit baryons.

Gell-Mann a proposé que l'isospin SU(2) ne soit pas une symétrie fondamentale, mais un sous-groupe d'une symétrie plus générale.

Cette symétrie plus étendue est le groupe SU(3). Dans ce cadre, les baryons ne se regroupent pas de manière arbitraire, mais selon une structure de symétrie précise et fortement contraignante.

Note. SU(3) est un groupe de Lie abstrait, analogue à SU(2), mais possédant huit générateurs au lieu de trois. Parmi ses représentations irréductibles figure une représentation de dimension huit, appelée représentation octet.

Les huit baryons $ p, n, \Lambda, \Sigma^+, \Sigma^0, \Sigma^-, \Xi^0, \Xi^- $ constituent précisément un octet de SU(3).

Ce schéma de classification est connu sous le nom de Eightfold Way.

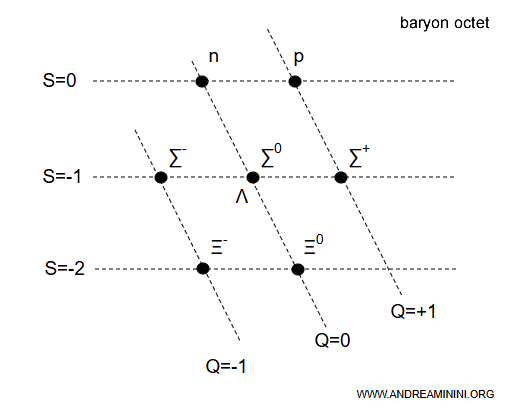
Dans cette perspective, les huit particules sont interprétées comme des états distincts d'une unique représentation de symétrie. Cette approche permet non seulement de clarifier les relations entre les baryons, mais aussi de prédire l'existence de particules encore inconnues.

Un exemple emblématique est la particule Ω⁻, dont l'existence a été prédite à partir du schéma SU(3) avant d'être confirmée expérimentalement.

De la même manière que \( p \) et \( n \) constituent les deux états d'un doublet d'isospin SU(2), les huit baryons correspondent aux différents états d'une représentation de SU(3).

La Eightfold Way et le modèle des quarks

La Eightfold Way est avant tout un outil de classification. Elle ne décrit pas directement la structure microscopique des hadrons.

À la fin des années 1950, il était déjà clair que de nombreux hadrons présentaient des propriétés similaires et pouvaient être regroupés en multiplets gouvernés par des symétries telles que SU(2) pour l'isospin et SU(3) pour la saveur.

À cette époque toutefois, ces régularités reposaient uniquement sur l'observation expérimentale. Leur origine physique et la structure interne des particules restaient encore inconnues.

La situation a profondément évolué avec l'introduction du modèle des quarks par Murray Gell-Mann et, indépendamment, par George Zweig. Ce modèle a établi que les hadrons ne sont pas élémentaires, mais des systèmes composites constitués de particules plus fondamentales appelées quarks.

Dans sa formulation initiale, le modèle introduit trois quarks légers : up (u), down (d) et strange (s).

quark	charge	isospin	étrangeté
u	\( +\tfrac23 \)	\( +\tfrac12 \)	0
d	\( -\tfrac13 \)	\( -\tfrac12 \)	0
s	\( -\tfrac13 \)	0	-1

Ces trois quarks \( (u, d, s) \) forment la représentation fondamentale de dimension trois de SU(3), souvent appelée triplet fondamental. Ils constituent le point de départ de toute la construction.

La symétrie de saveur SU(3) relie les quarks \( u \), \( d \) et \( s \), en les traitant comme équivalents vis-à-vis de l'interaction forte, à l'exception de leurs différences de masse. À partir de ces constituants, on peut comprendre de manière unifiée le spectre et les propriétés des hadrons.

En particulier, les baryons sont constitués de trois quarks :

$$ qqq $$

La combinaison de trois représentations fondamentales de SU(3) conduit à :

$$ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 $$

Cette décomposition rend compte du spectre baryonique observé :

• 10 correspond au décuplet de baryons de spin \( \tfrac32 \)
• 8 correspond à l'octet de baryons de spin \( \tfrac12 \)
• 1 correspond à un état singulet

L'existence du décuplet et de l'octet de baryons n'est donc pas une hypothèse ad hoc. Elle découle directement de la structure mathématique de la symétrie de saveur SU(3).

À titre d'exemple concret, l'octet de baryons peut être décrit explicitement en termes de contenu en quarks. Il est constitué de huit baryons formés à partir des quarks \( (u, d, s) \) :

Baryon	composition
p	uud
n	udd
\( \Lambda \)	uds
\( \Sigma^+ \)	uus
\( \Sigma^0 \)	uds
\( \Sigma^- \)	dds
\( \Xi^0 \)	uss
\( \Xi^- \)	dss

Ce schéma n'est pas le fruit du hasard. La symétrie de saveur SU(3) est particulièrement efficace précisément parce que les baryons sont constitués de trois quarks choisis dans l'ensemble \( (u, d, s) \).

Dans cette perspective, le modèle des quarks fournit le fondement microscopique de la Eightfold Way en introduisant les quarks \( (u, d, s) \), qui réalisent la représentation triplet fondamentale de SU(3).

Lorsque ces trois quarks sont combinés, les multiplets baryoniques initialement identifiés de manière empirique dans le cadre de la Eightfold Way apparaissent naturellement comme une conséquence directe de la structure de symétrie sous-jacente.

Note. La symétrie de saveur SU(3) n'est pas exacte, car les masses des quarks ne sont pas égales : $$ m_u \approx m_d \ll m_s $$ En conséquence, SU(3) n'est qu'une symétrie approchée. La présence de l'étrangeté introduit une brisure de symétrie, même si la structure globale des multiplets reste clairement identifiable. En revanche, la symétrie d'isospin SU(2) est généralement beaucoup plus précise.

Le décuplet de baryons

Après l'identification de l'octet de baryons de spin \( \tfrac12 \), les expériences ont révélé l'existence d'autres baryons présentant des propriétés très proches, mais dotés d'un spin total différent, égal à \( \tfrac32 \).

Ces nouveaux états ne pouvaient pas être intégrés à l'octet déjà connu. Leur organisation remarquablement régulière indiquait toutefois qu'il ne s'agissait ni de cas isolés ni d'anomalies expérimentales.

Il devenait alors clair que la symétrie SU(3) possède une structure bien plus riche et profonde que ce que l'on avait initialement envisagé.

Une analyse rigoureuse des configurations autorisées par la structure mathématique de SU(3) montre qu'en plus de l'octet (8), apparaissent naturellement d'autres représentations irréductibles, parmi lesquelles un décuplet (10) et un singulet (1) :

\[ 3 \otimes 3 \otimes 3 = 10 \oplus 8 \oplus 8 \oplus 1 \]

Cette décomposition ne repose pas sur une hypothèse physique arbitraire. Elle découle directement et nécessairement de la théorie des représentations.

Note. Autrement dit, dès lors que l'octet existe, le décuplet doit également exister, car tous deux émergent naturellement de la même structure mathématique sous-jacente.

Le décuplet de baryons décrit des états entièrement symétriques dans l'espace des saveurs. Il correspond donc à des baryons dont le spin total vaut \( \tfrac32 \).

Contrairement à l'octet, qui adopte une organisation hexagonale avec un état central, le décuplet se présente sous la forme d'un triangle équilatéral. Il comprend dix états répartis sur quatre niveaux bien distincts.

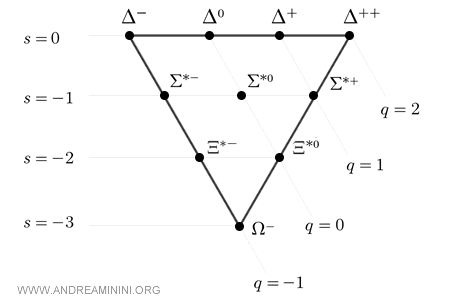
Note. La forme triangulaire n'est pas un simple choix graphique. Elle reflète une structure physique profonde : tous les baryons du décuplet possèdent des spins alignés, ce qui conduit à un spin total de \( \tfrac32 \). La symétrie entre les quarks y est donc maximale.

Le diagramme est construit à partir de deux nombres quantiques fondamentaux : l'étrangeté ( $ S $ ) et la charge électrique ( $ Q $ ).

En descendant dans le diagramme, l'étrangeté diminue, ce qui correspond à une augmentation progressive du nombre de quarks étranges dans la composition des particules.

Au sommet du triangle se trouvent quatre baryons \( \Delta \), dépourvus de quarks étranges et constitués uniquement de quarks up (u) et down (d).

• \( \Delta^{++} = uuu \)
• \( \Delta^+ = uud \)
• \( \Delta^0 = udd \)
• \( \Delta^- = ddd \)

Juste en dessous apparaissent trois baryons \( \Sigma \), chacun formé d'un quark étrange (s) et de deux quarks légers, up (u) et down (d) :

• \( \Sigma^{*+} = uus \)
• \( \Sigma^{*0} = uds \)
• \( \Sigma^{*-} = dds \)

La présence d'un quark étrange rompt légèrement la symétrie et se traduit par une augmentation de la masse par rapport aux baryons \( \Delta \).

Note. Nota. L’astérisque indique que la particule \( \Sigma \) se trouve dans un état de spin \( \tfrac32 \). Elle appartient à la même famille de baryons \( \Sigma \) que ceux de l’octet, mais correspond à une configuration de spin différente. Dans ce cas, le spin total ne vaut plus \( \tfrac12 \), mais \( \tfrac32 \), car les spins des trois quarks constitutifs sont entièrement alignés (↑↑↑). \[ \tfrac12 + \tfrac12 + \tfrac12 = \tfrac32 \] Cette configuration caractérise précisément les états du décuplet. En revanche, lorsque les spins ne sont pas tous alignés (↑↑↓, ↑↓↑ ou ↓↑↑), leur combinaison vectorielle conduit à un spin total plus faible: \[ \tfrac12 + \tfrac12 - \tfrac12 = \tfrac12 \] Dans ce cas, l’état obtenu possède un spin \( \tfrac12 \) et appartient à l’octet baryonique. La différence entre \( \Sigma \) et \( \Sigma^* \) ne réside donc pas dans leur contenu en quarks, qui est strictement identique, mais uniquement dans la manière dont leurs spins se couplent. Le même raisonnement s’applique à la particule \( \Xi^* \), qui représente la version de spin \( \tfrac32 \) du baryon \( \Xi \) appartenant à l’octet.

Au niveau suivant apparaissent deux baryons \( \Xi \), composés de deux quarks étranges et d'un quark léger. Leurs masses sont encore plus élevées.

• \( \Xi^{*0} = uss \)
• \( \Xi^{*-} = dss \)

Enfin, à la base du triangle se trouve une unique particule, le \( \Omega^- \), constituée exclusivement de quarks étranges :

\[ \Omega^- = sss \]

Cette particule occupe le niveau inférieur du décuplet et se caractérise par une étrangeté de -3, une charge électrique de -1 et un spin de \( \tfrac32 \).

La prédiction de la particule \( \Omega^- \)

La réussite la plus marquante de ce cadre théorique fut la prédiction de la particule \( \Omega^- \).

Située au sommet inférieur du décuplet, elle complète la structure symétrique anticipée par la théorie, alors même qu'elle n'avait pas encore été observée au moment de l'élaboration du modèle.

Sa découverte expérimentale en 1964 apporta une confirmation décisive de la validité de la symétrie de saveur SU(3).

Et ainsi de suite.