Principe de conservation de l’énergie
Le principe de conservation de l’énergie stipule que, dans un système isolé, la quantité totale d’énergie demeure constante au cours du temps.
En d’autres termes, l’énergie ne peut être ni créée ni détruite : elle ne fait que se transformer d’une forme en une autre. Ce principe constitue l’un des piliers fondamentaux de la physique moderne.
Il reste valable quelle que soit la forme d’énergie considérée (cinétique, potentielle, thermique, chimique, etc.) et s’applique à chaque conversion d’une forme en une autre.
- Énergie cinétique ($E_k$) : liée au mouvement
- Énergie potentielle ($E_p$) : liée à la position dans un champ de forces
- Énergie thermique : due à l’agitation des particules
- Énergie chimique, électrique, nucléaire, rayonnante, etc.
Il existe toutefois une condition essentielle : le système doit être un système isolé, c’est-à-dire sans échange d’énergie (ni de matière) avec son environnement.
Si cette condition n’est pas respectée, le bilan énergétique devient ouvert : de l’énergie peut entrer dans le système ou en sortir.
Loi de conservation de l’énergie
Dans un système mécanique simple (sans frottement), l’énergie totale reste inchangée et s’exprime ainsi :
$$ E = E_p + E_k = \text{constante} $$
où $E_p$ désigne l’énergie potentielle et $E_k$ l’énergie cinétique.
De manière plus générale, lorsque plusieurs formes d’énergie interviennent :
$$ E_{\text{totale}} = E_{\text{cinétique}} + E_{\text{potentielle}} + E_{\text{thermique}} + \dots = \text{constante} $$
L’énergie totale ne se conserve que si toutes les formes sont prises en compte et qu’aucun échange n’a lieu avec l’extérieur ; autrement dit, si le système est réellement isolé.
Exemples
Exemple 1 - Chute libre
Imaginons qu’une sphère soit lâchée d’une hauteur $h$, sans résistance de l’air.
Au départ, tant que la sphère est maintenue immobile, toute l’énergie est potentielle : $E_p = mgh$, sans contribution cinétique.
Une fois lâchée, l’énergie potentielle diminue au fur et à mesure de la descente, tandis que l’énergie cinétique augmente.
L’énergie ne disparaît pas : elle se convertit simplement d’une forme en une autre.
$$ E_k(t) + E_p(t) = \text{constante} $$
Juste avant de toucher le sol, l’énergie potentielle est pratiquement nulle ($E_p \approx 0$) et l’énergie cinétique atteint sa valeur maximale : $E_k = \tfrac{1}{2}mv^2$.
Exemple résolu. Considérons une sphère de masse $m = 0.5 \,\text{kg}$ lâchée d’une hauteur $h = 2 \,\text{m}$, en négligeant la résistance de l’air. Initialement, toute l’énergie est potentielle : $$ E_p = m g h = 0.5 \cdot 9.81 \cdot 2 \approx 9.81 \,\text{J} $$ tandis que l’énergie cinétique est nulle : $$E_k = 0 $$ Ainsi, l’énergie totale initiale du système est : $$E_{\text{tot}} = 9.81 \,\text{J}$$ À mi-hauteur $(h/2 = 1 \,\text{m})$, l’énergie se partage équitablement : la moitié reste potentielle et l’autre moitié est devenue cinétique. $$ E_p = m g h/2 = 0.5 \cdot 9.81 \cdot 1 = 4.905 \,\text{J} $$ $$ E_k = E_{\text{tot}} - E_p = 9.81 - 4.905 = 4.905 \,\text{J} $$ L’énergie totale reste inchangée : $$ E_{\text{tot}} = E_p + E_k = 4.905 \,\text{J} + 4.905 \,\text{J} = 9.81 \,\text{J} $$ La vitesse à cette hauteur est : $$ E_k = \tfrac{1}{2} m v^2 \;\;\Rightarrow\;\; v = \sqrt{\tfrac{2 E_k}{m}} = \sqrt{\tfrac{2 \cdot 4.905}{0.5}} \approx 4.43 \,\text{m/s} $$ Juste avant l’impact, l’énergie potentielle est quasiment nulle : $$ E_p \approx 0 $$ tandis que l’énergie cinétique atteint sa valeur maximale : $$ E_k = E_{\text{tot}} = 9.81 \,\text{J} $$ La vitesse d’impact est alors : $$ v = \sqrt{\tfrac{2 E_k}{m}} = \sqrt{\tfrac{2 \cdot 9.81}{0.5}} = \sqrt{39.24} \approx 6.26 \,\text{m/s} $$ En résumé, tout au long de la chute, la somme de l’énergie potentielle et cinétique demeure constante : $$ E_{\text{totale}} = E_p + E_k = 9.81 \,\text{J} = \text{constante} $$ Aucune énergie ne se perd : elle se transforme uniquement d’énergie potentielle gravitationnelle en énergie cinétique.
Exemple 2 - Pendule oscillant
Dans un pendule idéal (sans frottement), l’énergie potentielle est maximale aux extrémités, lorsque la vitesse est nulle et que le pendule s’immobilise avant d’inverser son mouvement.
En position la plus basse, l’énergie cinétique est maximale, car le pendule atteint sa vitesse la plus élevée.
Une fois encore :
$$ E_k + E_p = \text{constante} $$
Remarque. Si l’on prend en compte la résistance de l’air, l’énergie mécanique se transforme progressivement en chaleur au lieu de se conserver intégralement. Toutefois, la somme globale (mécanique + thermique) reste constante. Le principe de conservation de l’énergie demeure universellement valable.
Exemple 3 - Conversion d’énergie dans une centrale électrique
Dans une centrale thermique, l’énergie chimique du combustible est libérée lors de la combustion.
Cette combustion produit des gaz chauds qui transmettent leur énergie thermique à un fluide de travail (généralement de l’eau), le transformant en vapeur sous haute pression.
La vapeur entraîne une turbine, convertissant l’énergie thermique en énergie mécanique de rotation.
La turbine est reliée à un alternateur, qui transforme l’énergie mécanique en énergie électrique par induction électromagnétique.
À chaque étape, l’énergie totale se conserve : elle change seulement de forme.
Remarque. Toute l’énergie thermique ne se convertit pas ; une partie est inévitablement dissipée sous forme de chaleur résiduelle. Néanmoins, dans un système isolé, la somme de l’électricité produite et de la chaleur dissipée reste constante. Le principe de conservation n’est jamais remis en cause.
Conservation de l’énergie en physique des particules
Le principe de conservation de l’énergie est véritablement universel : il s’applique à toutes les interactions fondamentales. Que l’on considère une désintégration, une collision ou une annihilation, l’énergie totale avant et après le processus demeure inchangée.
Un exemple emblématique est la désintégration bêta. Dans ce phénomène, un neutron se transforme en proton, en électron et en antineutrino $ n \;\;\longrightarrow\;\; p + e^- + \bar{\nu}_e $, par l’intermédiaire de l’interaction faible.
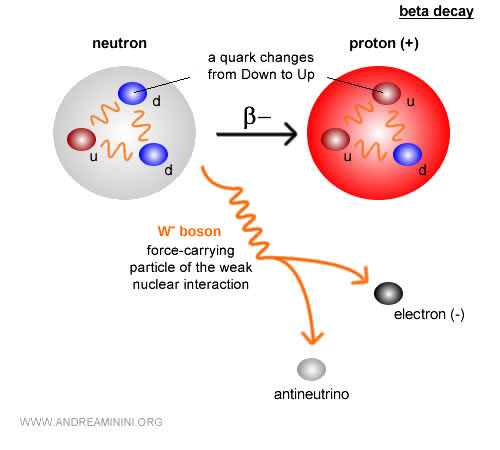
Ici, la masse au repos n’est pas conservée : la masse du neutron excède la somme des masses du proton, de l’électron et de l’antineutrino.
Cette masse « manquante » ne s’évanouit pas : elle se convertit en énergie cinétique des particules produites.
L’essentiel est que ce qui reste constant, c’est l’énergie totale, et non la masse. C’est précisément ce qu’énonce la célèbre équation d’Einstein :
$$ E = mc^2 $$
Autrement dit, une partie de la masse au repos peut se transformer en énergie cinétique ou en rayonnement.
L’inverse est également possible : l’énergie peut se matérialiser sous forme de masse, par exemple lors de la création d’une paire quark-antiquark.
Ainsi, dans les réactions nucléaires ou les désintégrations de particules, la masse peut sembler « disparaître » ou « apparaître », tandis que le bilan énergétique global reste strictement préservé.
Remarque. Outre l’énergie, d’autres grandeurs se conservent dans les interactions fondamentales : la quantité de mouvement, la charge électrique, la charge de couleur en QCD, les nombres leptonique et baryonique (dans certains cas), ou encore le spin total.
Conservation de l’énergie dans l’univers
Le principe de conservation de l’énergie s’applique avec une grande fiabilité dans tous les contextes locaux, de la mécanique quantique non relativiste jusqu’à la théorie quantique des champs (QFT).
En relativité générale en revanche, la situation est plus subtile. Dans un espace-temps courbe, il n’existe pas toujours de définition unique et rigoureuse d’une « énergie totale » pour l’univers.
La raison tient au théorème de Noether, qui relie la conservation de l’énergie à l’invariance par translation temporelle. Dans un univers en expansion, cette symétrie globale du temps est rompue.
Un exemple classique est l’expansion cosmique : la densité d’énergie du rayonnement décroît plus vite que celle de la matière parce que c’est l’espace lui-même qui se dilate. Il ne s’agit pas d’un « transfert » d’énergie entre composantes, mais d’une conséquence géométrique de l’expansion de l’espace-temps.
C’est pourquoi de nombreux cosmologistes considèrent que parler de « conservation de l’énergie totale de l’univers » est, au mieux, ambigu. Ce qui se conserve réellement, c’est l’énergie au niveau local, dans chaque processus physique étudié dans un référentiel donné.
À l’échelle cosmologique, la question reste ouverte et demeure intimement liée au problème, encore irrésolu, de la définition cohérente de l’énergie en relativité générale.
Fondements théoriques
La conservation de l’énergie découle directement de l’invariance des lois physiques par translation temporelle : les lois restent les mêmes que l’expérience soit réalisée aujourd’hui, demain ou dans des siècles.
Elle n’est donc pas une simple règle empirique issue de l’observation.
Elle résulte d’une symétrie fondamentale de la nature.
En physique, le terme « symétrie » ne désigne pas la symétrie visuelle de la géométrie courante, mais une transformation qui laisse inchangé le comportement d’un système physique.
Par exemple, si un système évolue de la même façon aujourd’hui, demain ou dans cent ans, cela signifie que les lois qui le régissent sont indépendantes du temps : elles sont invariantes par translation temporelle.
Cette invariance temporelle garantit que l’énergie totale d’un système demeure constante au cours de son évolution.
Le lien profond entre symétries et grandeurs conservées a été établi en 1918 par Emmy Noether. Selon le théorème de Noether :
À toute symétrie continue d’un système physique correspond une grandeur conservée.
Dans le cas de l’énergie, la symétrie pertinente est l’invariance par translation temporelle : si les lois de la physique ne dépendent pas du temps, alors l’énergie se conserve.
Ce principe vaut dans tout le champ de la physique, de la mécanique classique aux théories les plus avancées de la physique quantique.
Et ainsi de suite.