Nombres leptoniques

Comme il existe trois familles de leptons, la physique des particules introduit trois nombres leptoniques distincts :

• Nombre électronique $L_e$
• Nombre muonique $L_\mu$
• Nombre tauique $L_\tau$

Dans chaque famille, les leptons ont une valeur de $+1$, tandis que leurs antiparticules portent $-1$.

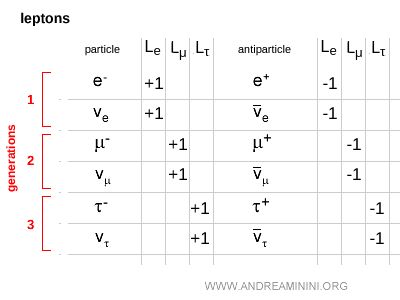
Par exemple, dans la première famille de leptons, l’électron $ e^- $ et le neutrino électronique $ \nu_e $ possèdent le nombre leptonique électronique $ L_e = +1 $, tandis que leurs antiparticules - le positon $ e^+ $ et l’antineutrino électronique $ \bar{\nu}_e $ - ont $ L_e = -1 $. Tous les autres nombres leptoniques sont égaux à zéro. 

Conservation du nombre leptonique

Les nombres leptoniques se conservent dans toutes les interactions fondamentales.

Autrement dit, la somme totale des nombres leptoniques doit être la même avant et après une réaction.

Tout processus qui enfreindrait cette règle est interdit par la nature, du moins dans le cadre du Modèle Standard.

• Interaction forte
  La force forte n’interagit pas avec les leptons : leurs nombres leptoniques restent donc inchangés. Dans une interaction purement forte, aucun lepton n’est ni créé ni détruit.
• Interaction électromagnétique
  La force électromagnétique agit sur les leptons chargés (comme l’électron), mais elle ne modifie pas la famille à laquelle ils appartiennent. Les nombres leptoniques demeurent donc constants.
• Interaction faible
  L’interaction faible peut transformer un lepton en un autre au sein de sa propre famille. Cependant, le nombre leptonique de chaque famille est conservé séparément. Tout processus qui violerait cette conservation n’a tout simplement pas lieu dans la nature.
  

  Remarque. L’interaction faible conserve indépendamment les nombres leptoniques des trois familles. Par exemple, un électron ou un neutrino électronique (première génération) ne peut pas se transformer en muon ou en tau (deuxième ou troisième génération), et réciproquement. C’est pourquoi l’on distingue trois nombres leptoniques ($ L_e,\quad L_\mu,\quad L_\tau $), chacun restant conservé dans les processus faibles. Cette conservation stricte est caractéristique des leptons. Les quarks, en revanche, obéissent à une logique différente : dans leurs interactions faibles, ils peuvent se mélanger entre générations grâce à la matrice CKM (Cabibbo - Kobayashi - Maskawa), si bien qu’il n’existe pas de « nombres quarkiques » conservés de façon analogue à $L_e$, $L_\mu$ ou $L_\tau$.

Exemple

Le muon négatif $\mu^-$ appartient à la deuxième génération de leptons.

Dans le vide, il se désintègre spontanément par interaction faible en trois particules : un électron ($ e^- $), un antineutrino électronique ( $ \bar{\nu}_e $ ) et un neutrino muonique ( $ \nu_\mu $ ).

$$ \mu^- \rightarrow e^- + \bar{\nu}_e + \nu_\mu $$

Pour vérifier si cette désintégration est permise, examinons les nombres leptoniques de chacune des particules en présence :

$$ \underset{L_\mu = +1}{\mu^-} \;\;\rightarrow\;\; \underset{L_e = +1}{e^-} \;+\; \underset{L_e = -1}{\bar{\nu}_e} \;+\; \underset{L_\mu = +1}{\nu_\mu} $$

Vérification de la conservation pour chaque famille leptonique :

• Nombre électronique ( $ L_e $ )
  Initialement : $$ L_e^{\text{initial}} = 0 $$ Après la désintégration : $$ L_e^{\text{final}} = +1 \ (\text{de } e^-) + (-1) \ (\text{de } \bar{\nu}_e) = 0 $$ Le nombre électronique est donc conservé. $$ L_e^{\text{initial}} = L_e^{\text{final}} = 0 $$
• Nombre muonique ( $L_\mu$ )
  Initialement : $$ L_\mu^{\text{initial}} = +1 \ (\text{du } \mu^-) $$ Après la désintégration : $$ L_\mu^{\text{final}} = +1 \ (\text{du } \nu_\mu) $$ Le nombre muonique est donc conservé. $$ L_\mu^{\text{initial}} = L_\mu^{\text{final}} = +1 $$
• Nombre tauique ( $L_\tau $ )
  Aucun lepton tau n’intervient : le nombre tauique reste nul avant comme après. $$ L_\tau^{\text{initial}} = L_\tau^{\text{final}} = 0 $$

On voit ainsi que la désintégration du muon respecte la conservation indépendante des trois nombres leptoniques, ce qui explique qu’elle se produise effectivement dans la nature.

Exemple 2

Considérons à présent une autre désintégration, purement hypothétique :

$$ \mu^- \rightarrow e^- + \gamma $$

Les seuls nombres leptoniques non nuls des particules en jeu sont :

$$ \underset{L_\mu = +1}{\mu^-} \;\;\rightarrow\;\; \underset{L_e = +1}{e^-} + \gamma $$

Dans ce cas, la conservation des nombres leptoniques est violée à la fois pour $L_e$ et pour $L_\mu$, puisqu’aucun neutrino n’apparaît pour compenser la variation.

C’est pourquoi une telle désintégration n’existe pas dans la nature ou, si elle se produisait, ce serait avec une probabilité si infime qu’elle n’a encore jamais été observée.

Remarques finales

Quelques compléments à propos des nombres leptoniques :

• Oscillations de neutrinos et possibles violations
  La découverte des oscillations de neutrinos a montré qu’à grande distance, un neutrino peut se transformer en un autre type de la même famille. Cela implique une légère violation de la conservation des nombres leptoniques individuels, même si le nombre leptonique total reste inchangé : $$L = L_e + L_\mu + L_\tau$$ Si ce phénomène venait à être pleinement confirmé, il constituerait un indice solide d’une physique nouvelle au-delà du Modèle Standard.

Le débat demeure donc ouvert…