Loi de conservation de la quantité de mouvement

La loi de conservation de la quantité de mouvement stipule que, dans un système isolé (c’est-à-dire sans forces extérieures), la quantité totale de mouvement $ \vec{P} $ demeure constante : $$ \vec{P} = \sum_i m_i \vec{v}_i $$ où $m$ désigne la masse de chaque particule et $\vec{v}$ sa vitesse.

La quantité de mouvement résulte de l’association entre masse et vitesse :

$$ \vec{p} = m \vec{v} $$

Cette grandeur exprime la capacité d’un corps en mouvement à exercer une influence lors d’une interaction, car elle dépend à la fois de sa masse et de sa vitesse.

Ainsi, un camion possède une masse considérable et, même en avançant lentement, il dispose d’une quantité de mouvement très importante. À l’inverse, une balle de ping-pong est si légère que, même lancée à grande vitesse, sa quantité de mouvement reste quasiment négligeable.

Selon la loi de conservation de la quantité de mouvement, si aucune force extérieure n’agit sur un système, la quantité totale de mouvement avant et après toute interaction reste inchangée :

$$ \vec{P}_{\text{initiale}} = \vec{P}_{\text{finale}} $$

La quantité de mouvement est donc une grandeur conservée, mais uniquement dans des systèmes fermés et isolés.

Un exemple simple

Imaginons deux patineurs sur une glace parfaitement lisse.

Au départ, ils sont immobiles, et la quantité totale de mouvement est nulle. Lorsqu’ils se repoussent, l’un glisse vers la droite et l’autre vers la gauche.

La quantité de mouvement de l’un est égale et opposée à celle de l’autre, de sorte que le total reste nul, comme au début.

Autrement dit, si la force extérieure résultante est nulle ($\vec{F}_{\text{ext}}=0$), alors :

$$ \frac{d\vec{P}}{dt} = 0 \quad \Rightarrow \quad \vec{P}_{\text{initiale}} = \vec{P}_{\text{finale}} $$

Exemple 2

Considérons deux boules de billard, chacune de 200 grammes, se déplaçant avec des vitesses initiales différentes :

• Boule A : $m_A = 0.2 \,\text{kg}$, vitesse initiale $v_A = 5 \,\text{m/s}$.
• Boule B : $m_B = 0.2 \,\text{kg}$, initialement au repos ($v_B = 0$).

La boule A avance à 5 m/s tandis que la boule B reste immobile.

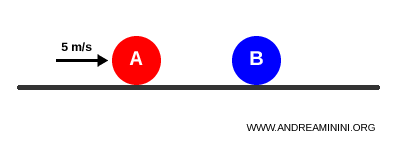
Avant la collision, la quantité totale de mouvement du système est de 1 kg·m/s :

$$ p_{\text{tot}} = m_A v_A + m_B v_B = 0.2 \cdot 5 + 0.2 \cdot 0 = 1.0 \,\text{kg·m/s} $$

Lorsque la boule A percute de plein fouet la boule B :

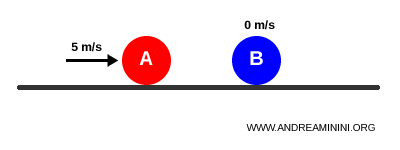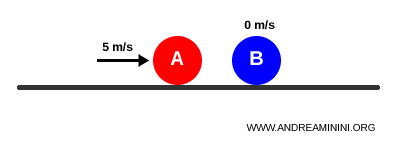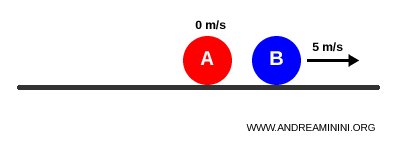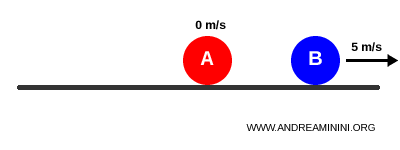
Après une collision élastique, la boule A s’arrête et la boule B repart à 5 m/s :

$$ v_A' = 0 \qquad v_B' = 5 \,\text{m/s} $$

La quantité totale de mouvement reste inchangée :

$$ p_{\text{tot, finale}} = m_A v_A' + m_B v_B' = 0.2 \cdot 0 + 0.2 \cdot 5 = 1.0 $$

Ainsi, qu’elles soient élastiques ou inélastiques, les collisions conservent la quantité totale de mouvement du système.

Exemple 3

Considérons maintenant un fusil de masse $m_f = 4 \,\text{kg}$ et une balle de masse $m_p = 0.02 \,\text{kg}$.

Au départ, le fusil est immobile, et la quantité totale de mouvement est nulle :

$$ p_{\text{initial}} = 0 $$

Au tir, la balle quitte le canon à une vitesse de $v_p = 400 \,\text{m/s}$.

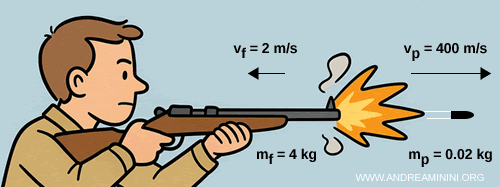
La quantité de mouvement de la balle est alors :

$$ p_p = m_p \cdot v_p = 0.02 \cdot 400 = 8 \,\text{kg·m/s} $$

Par conservation, le fusil acquiert une quantité égale et opposée :

$$ p_f = -8 \,\text{kg·m/s} $$

Ce qui correspond à une vitesse de recul de 2 m/s :

$$ v_f = \frac{p_f}{m_f} = \frac{-8}{4} = -2 \,\text{m/s} $$

C’est l’origine du recul caractéristique des armes à feu.

Globalement, la quantité totale de mouvement reste nulle :

$$ p_{\text{tot}} = p_p + p_f = 8 - 8 = 0 $$

La répartition, en revanche, est très inégale : la balle légère atteint une vitesse considérable, tandis que le fusil massif recule lentement dans le sens opposé.

Fondement théorique

La conservation de la quantité de mouvement découle d’un principe plus profond : la symétrie de l’espace.

On dit que l’espace est homogène lorsque les lois de la physique sont identiques en tout point.

En d’autres termes, déplacer un système de quelques mètres vers la droite ou vers la gauche ne modifie en rien les équations qui régissent son mouvement.

Le théorème de Noether établit qu’à toute symétrie continue d’un système physique correspond une grandeur conservée :

• Symétrie temporelle
  L’invariance par translation dans le temps entraîne la conservation de l’énergie.
• Symétrie spatiale
  L’invariance par translation dans l’espace entraîne la conservation de la quantité de mouvement.
• Symétrie rotationnelle
  L’invariance par rotation entraîne la conservation du moment cinétique.

L’invariance par translation dans l’espace garantit donc la conservation de la quantité de mouvement.

Et ainsi de suite.