Voisinage d’un point

Un voisinage d'un point \( x_0 \) est un ensemble de points situés suffisamment près de \( x_0 \). De manière intuitive, il permet d'identifier quels points sont considérés comme « proches » d'un point donné.

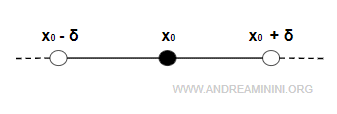
Le symbole \( \delta \) désigne un nombre réel strictement positif arbitraire. Il joue le rôle de paramètre et fixe la taille du voisinage.

En analyse réelle élémentaire, un voisinage d'un point \( x_0 \) est le plus souvent représenté par un ensemble $ I_0 $ de points appartenant à un intervalle ouvert. Les bornes de cet intervalle sont exclues et, selon la définition retenue, le point \( x_0 \) peut ou non faire partie du voisinage.

Pour cette raison, il est important de distinguer clairement deux notions étroitement liées, mais conceptuellement différentes.

• Voisinage ponctué
  Un voisinage ponctué de $ x_0 $, défini pour $ \delta > 0 $, est un voisinage qui exclut explicitement le point $ x_0 $. Il est défini comme l'union de deux intervalles ouverts $$  I_{ \delta } (x_0) = (x_0 - \delta, x_0)\ \cup\ (x_0, x_0 + \delta) $$
• Voisinage contenant le point
  Un voisinage de $ x_0 $ qui contient le point lui-même est défini, pour $ \delta > 0 $, comme l'intervalle ouvert $$  I_{ \delta } (x_0) = (x_0 - \delta, x_0 + \delta)  $$ Il peut aussi s'écrire en notation ensembliste $$ I_{ \delta } (x_0) = \{ x \in \mathbb{R} \mid  x_0 - \delta < x < x_0 + \delta \} $$ ou, de manière équivalente, $$ I_{ \delta } (x_0) = \{ x \in \mathbb{R} \mid |x-x_0| < \delta \} $$

Remarque. En analyse mathématique, lorsqu'on parle d'un « voisinage de \( x_0 \) » sans autre précision, on désigne presque toujours un voisinage ponctué. Cette convention reflète le fait que, dans l'étude des limites et de la continuité, l'intérêt porte sur le comportement d'une fonction arbitrairement près d'un point, et non sur sa valeur exacte en ce point. Cette distinction est essentielle pour une compréhension rigoureuse de l'analyse.

Un exemple concret

Supposons que le point x₀ soit égal à dix.

$$ x_0 = 10 $$

Fixons ensuite la valeur de delta à deux.

$$ δ=2 $$

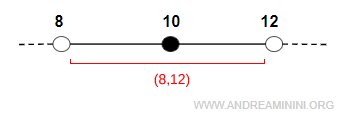
Le voisinage de $ x_0 $ qui contient le point est alors l'intervalle ouvert compris entre huit et douze.

$$ I_0 = (x_0-δ, x_0+δ) $$

$$ I_0 = (10-2, 10+2) $$

$$ I_0 = (8, 12) $$

Il s'agit d'un intervalle ouvert qui contient tous les nombres réels strictement supérieurs à huit et strictement inférieurs à douze. Comme le voisinage est défini de manière à contenir le point, la valeur $ x_0 = 10 $ appartient bien à cet ensemble.

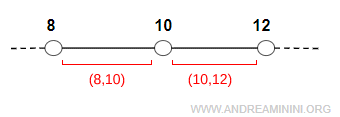
À l'inverse, le voisinage ponctué de $ 10 $ n'inclut pas le point \( x_0 = 10 \). Il ne s'agit pas d'un intervalle unique, mais de l'union de deux intervalles ouverts disjoints :

$$ I_0 = (x_0 - \delta, x_0)\ \cup\ (x_0, x_0 + \delta) $$

$$ I_0 = (10 - 2, 10)\ \cup\ (10, 10 + 2) $$

$$ I_0 = (8, 10)\ \cup\ (10, 12) $$

Dans ce cas, le point $ x_0 = 10 $ n'appartient pas au voisinage.

Remarque. Sauf indication contraire, un voisinage n'est pas nécessairement symétrique par rapport à $ x_0 $. On peut par exemple définir un voisinage à l'aide de deux réels strictement positifs distincts $ \delta_1 \ne \delta_2 $ sous la forme $$ (x_0-δ_1, x_0+δ_2) $$ Dans ce cas, le point $ x_0 $ n'est plus le milieu de l'intervalle. Certains ouvrages réservent l'expression voisinage de rayon $ \delta $ au cas symétrique $ \delta_1 = \delta_2 $. Dans le cadre de $ \mathbb{R}^2 $, on emploie également le terme « voisinage circulaire » pour désigner des voisinages dans le plan. Afin d'éviter toute ambiguïté, les termes « voisinage » et « voisinage ponctué » sont ici réservés aux points de la droite réelle, tandis que entorno circular est utilisé pour les voisinages dans le plan.

Voisinages droit et gauche

Dans de nombreuses situations, il est utile d'étudier le comportement d'une fonction en se limitant aux points situés uniquement à droite ou uniquement à gauche d'un point donné.

De cette approche découlent naturellement les notions de voisinage droit et de voisinage gauche.

• Voisinage droit
  Le voisinage droit d'un point \( x_0 \), noté \( I_0^+ \), est l'ensemble des nombres réels strictement supérieurs à \( x_0 \) et appartenant à l'intervalle ouvert $ ( x_0, x_0+ \delta ) $, avec \( \delta > 0 \). $$ I_0^+ = (x_0, x_0 + \delta) $$
• Voisinage gauche
  Le voisinage gauche d'un point \( x_0 \), noté \( I_0^- \), est l'ensemble des nombres réels strictement inférieurs à \( x_0 \) et appartenant à l'intervalle ouvert $ ( x_0- \delta, x_0 ) $, avec \( \delta > 0 \). $$ I_0^- = (x_0 - \delta, x_0) $$

Ces notions jouent un rôle central dans l'étude des limites latérales et dans l'analyse de la continuité des fonctions.

Par exemple, si \( x_0 = 2 \) et \( \delta = 0.5 \), le voisinage droit est \[ I_0^+ = (2, 2.5) \] tandis que le voisinage gauche est \[ I_0^- = (1.5, 2) \]

Voisinages de l'infini

Dans certains contextes, il est pertinent de considérer des intervalles ouverts qui ne sont bornés ni supérieurement ni inférieurement.

Ces ensembles sont appelés voisinages de l'infini.

• Voisinage de moins l'infini
  Un voisinage de moins l'infini est un intervalle ouvert non borné inférieurement qui contient tous les nombres réels strictement inférieurs à un réel fixé \( a \).  \[ I(-\infty) = (-\infty, a) = \{ x \in \mathbb{R} \mid x < a \} \]
• Voisinage de plus l'infini
  Un voisinage de plus l'infini est un intervalle ouvert non borné supérieurement qui contient tous les nombres réels strictement supérieurs à un réel fixé \( a \). \[ I(+\infty) = (a, +\infty) = \{ x \in \mathbb{R} \mid x > a \} \]

Chaque fois que le symbole de l'infini est utilisé, il est indispensable d'en préciser explicitement le signe, car le symbole générique \( \infty \) peut désigner aussi bien \( -\infty \) que \( +\infty \).

Par exemple, si \( a = 3 \), un voisinage de moins l'infini est \[ I(-\infty) = (-\infty, 3) \] tandis qu'un voisinage de plus l'infini est \[ I(+\infty) = (3, +\infty) \] Numériquement, le nombre \( -1000 \) appartient au voisinage de moins l'infini, tandis que le nombre \( 10 \) appartient au voisinage de plus l'infini.

Notes

Observations complémentaires sur les voisinages

• L'intersection et l'union de deux voisinages de $ x_0 $ sont elles-mêmes des voisinages de $ x_0 $

Et ainsi de suite.