Distanța dintre mulțimi

Distanța dintre două mulțimi \(A\) și \(B\), într-un spațiu metric \((X, d)\), reprezintă cea mai mică distanță posibilă între un punct al mulțimii \(A\) și un punct al mulțimii \(B\) : $$ d(A, B) = \inf \{ d(a, b) \mid a \in A ,\ b \in B \}, $$ unde \(d(a, b)\) este distanța dintre cele două puncte, iar \(\inf\) (infimul) înseamnă „cea mai mică limită inferioară” a tuturor acestor distanțe.

Pe scurt, luăm toate perechile posibile formate dintr-un punct al lui \(A\) și unul al lui \(B\), măsurăm distanțele dintre ele și alegem cea mai mică dintre ele. Aceasta este distanța dintre cele două mulțimi.

Conceptul ne spune cât de aproape pot fi două mulțimi una de cealaltă - chiar și atunci când nu se ating efectiv.

Observație : Distanța dintre mulțimi nu indică dacă ele se intersectează, ci doar cât de „strâns” pot fi apropiate elementele lor.

Când este distanța egală cu zero?

O valoare nulă, \(d(A, B) = 0\), înseamnă că există puncte din cele două mulțimi care pot fi aduse arbitrar de aproape. Cu toate acestea, nu înseamnă că se suprapun sau că au un punct comun.

De fapt, două mulțimi pot avea distanța zero și totuși să fie complet separate, adică \(A \cap B = \emptyset\).

Exemple simple

Pentru a înțelege mai bine, să luăm câteva cazuri pe axa numerelor reale, cu distanța uzuală \(d(x_1, x_2) = |x_1 - x_2|\).

A] Cazul 1 - un punct și un interval

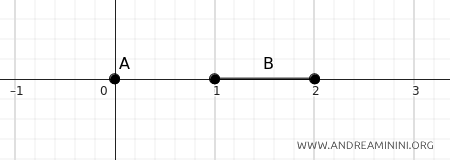
Dacă \(A = \{0\}\) și \(B = [1, 2]\), distanța dintre ele este \(1\):

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(0, 1) = 1 $$

Punctul \(0\) se află exact la o unitate distanță de punctul cel mai apropiat din \(B\), adică de \(1\).

B] Cazul 2 - două intervale care se ating

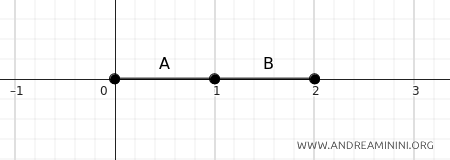
Dacă \(A = [0, 1]\) și \(B = [1, 2]\), distanța este zero:

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = d(1, 1) = 0 $$

De ce? Pentru că cele două intervale au un punct comun, \(1\). Așadar, nu mai există nicio „distanță” între ele.

Intersecția lor este clară:

$$ A \cap B = \{ 1 \} $$

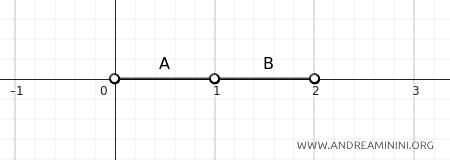
C] Cazul 3 - două intervale deschise, fără puncte comune

Dacă \(A = (0, 1)\) și \(B = (1, 2)\), pare că ar trebui să existe o „mică distanță” între ele. Totuși, rezultatul este tot zero:

$$ d(A, B) = \inf \{ d(a, b) \mid a \in A, b \in B \} = 0 $$

Deși intervalele nu se ating, putem alege puncte \(a \in A\) și \(b \in B\) cât de aproape dorim de valoarea \(1\), fără a o atinge niciodată. Cu cât le alegem mai aproape de margine, cu atât distanța \(|a - b|\) scade.

Astfel, deși \(A\) și \(B\) nu conțin punctul \(1\), putem face distanța dintre elementele lor oricât de mică. În consecință:

$$ d(A, B) = |1 - 1| = 0 $$

Ce învățăm de aici

Două mulțimi pot fi „infinit de apropiate” fără a avea vreun punct comun. Distanța nulă nu înseamnă identitate sau contact, ci doar posibilitatea de apropiere nelimitată între elementele lor.

Pe scurt : Distanța nulă exprimă o apropiere potențială, nu o intersecție reală. Este o noțiune esențială în analiza metrică, folosită pentru a descrie cum pot „tinde” două mulțimi una spre cealaltă fără să se atingă.