Réduction du nombre de côtés dans les polygones convexes
Tout polygone convexe est équivalent à un autre polygone possédant moins de côtés tout en conservant la même aire.
L'idée centrale est simple : il est possible de transformer un polygone en un autre, de forme différente et avec un nombre de côtés inférieur, en procédant par décomposition et réassemblage, sans jamais modifier l'aire.
Le triangle constitue la seule exception. Il n'existe pas de polygone à deux côtés et, par définition, tout polygone comporte au moins trois côtés.
Ce résultat est fondamental en géométrie plane. Il montre que l'aire dépend uniquement de la surface occupée, et non de la forme précise du polygone.
Remarque : Le principe s'applique aussi bien aux polygones convexes qu'aux polygones concaves. Toutefois, dans le cas convexe, la démarche est généralement plus simple et plus intuitive. Les polygones concaves peuvent nécessiter des découpages et des réassemblages plus complexes afin de traiter les zones de concavité.
Construire un polygone équivalent avec un côté de moins
Il existe plusieurs manières de réduire le nombre de côtés d'un polygone.
Une méthode courante consiste à le décomposer en figures plus simples, puis à les réassembler selon une nouvelle disposition.
Parmi les approches les plus accessibles, on peut exploiter les diagonales du polygone.
Considérons un polygone quelconque, régulier ou irrégulier. Pour fixer les idées, prenons le cas d'un hexagone.
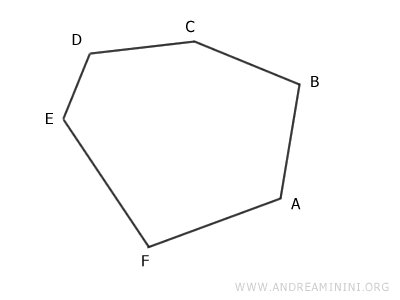
On commence par tracer une diagonale reliant deux sommets séparés par un sommet intermédiaire.
Par exemple, on trace la diagonale reliant A et C, le sommet B se trouvant entre les deux.
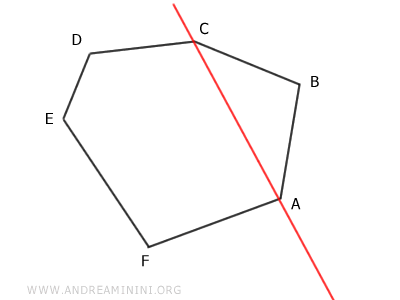
On translate ensuite cette diagonale de façon à la faire passer par le sommet intermédiaire B.
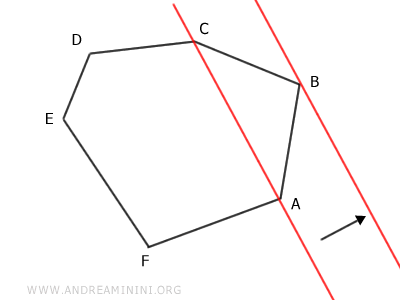
On prolonge alors l'un des côtés issus de A ou de C jusqu'à ce qu'il rencontre cette droite.
Dans notre exemple, on prolonge le côté AF jusqu'au point A'.
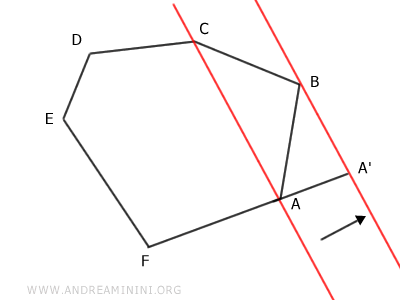
On trace ensuite le segment A'C, qui relie le point A' au sommet C. Cette opération permet de supprimer le sommet B du polygone initial.
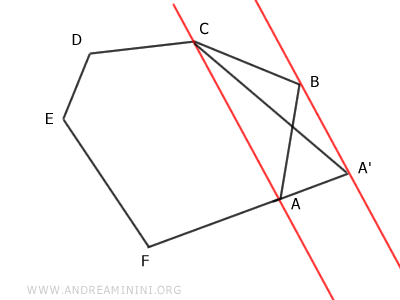
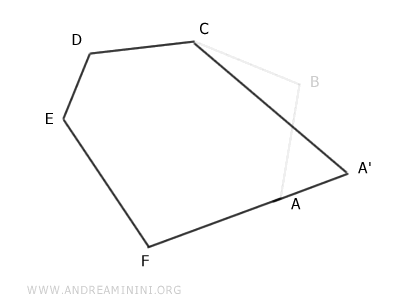
On obtient ainsi un polygone A'CDEF à cinq côtés, c'est-à-dire un pentagone.
Ce pentagone est équivalent à l'hexagone de départ, au sens où leurs aires sont identiques.
Démonstration : Pour le vérifier, comparons les triangles AA'C et ABC.
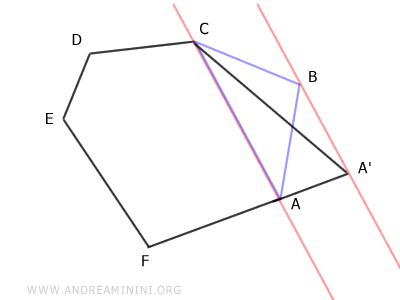
Ces deux triangles ont la même base AC et la même hauteur, puisque AA'≅BB'. Ils ont donc la même aire, conformément au résultat classique selon lequel deux triangles de même base et de même hauteur sont équivalents en aire.
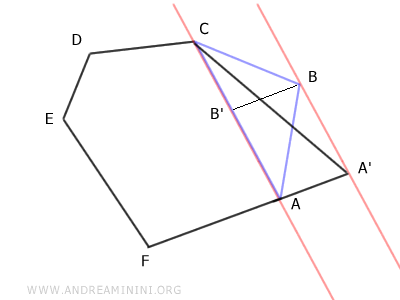
On peut alors écrire que l'hexagone est constitué du polygone ACDEF et du triangle ABC : $$ ABCDEF \doteq ACDEF + ABC $$ De même, le pentagone A'CDEF est constitué du polygone ACDEF et du triangle AA'C : $$ A'CDEF \doteq ACDEF + AA'C $$ Les triangles ABC et AA'C étant équivalents, l'hexagone et le pentagone sont des polygones équidécomposables, c'est-à-dire décomposables en figures de même aire : $$ ABCDEF \doteq ACDEF + ABC \doteq ACDEF + AA'C \doteq A'CDEF $$ $$ ABCDEF \doteq A'CDEF $$ Ainsi, l'hexagone ABCDEF et le pentagone A'CDEF sont équivalents.
En répétant le même raisonnement, on peut réduire le pentagone A'CDEF à un quadrilatère équivalent C'DEF, possédant quatre côtés.
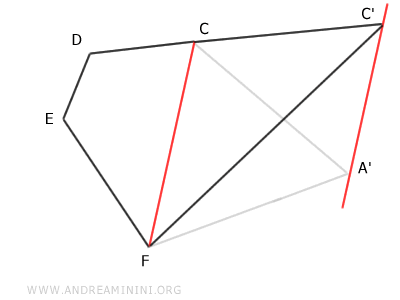
Enfin, ce quadrilatère peut à son tour être réduit à un triangle équivalent C'D'F, à trois côtés.
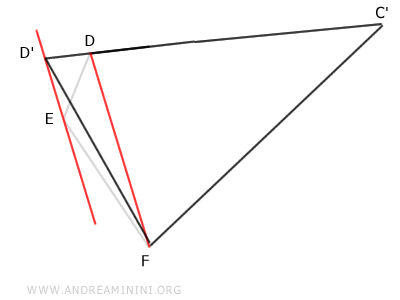
On en déduit que tout polygone convexe peut, par étapes successives, être ramené à un triangle équivalent.
Remarque : La méthode présentée ici, basée sur l'utilisation de diagonales, ne constitue pas une procédure formelle de la géométrie euclidienne axiomatique. En pratique, la conservation de l'aire lors d'un changement du nombre de côtés repose sur des techniques rigoureuses de découpage et de réassemblage, et non sur le simple tracé ou déplacement de diagonales.
Observations
Quelques points méritent d'être soulignés :
- Polygones concaves
Pour les polygones concaves, il n'est pas toujours possible de réduire le nombre de côtés sans modifier l'aire, du moins dans le cadre de la géométrie euclidienne classique.
Et ainsi de suite.