Polygones équivalents

On appelle polygones équivalents deux polygones qui possèdent exactement la même aire, même s'ils n'ont pas du tout la même forme.

Cette idée est au cœur de nombreuses techniques en géométrie. Deux figures peuvent sembler très différentes, mais si elles couvrent la même surface dans le plan, elles sont considérées comme équivalentes. Cette approche permet d'étudier les polygones sous un angle plus général que celui de leur simple apparence.

 

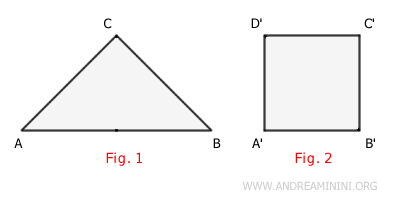
L'équivalence se concentre uniquement sur l'aire, ce qui signifie que toutes les variations de forme ou de proportions deviennent secondaires. Deux polygones peuvent donc être réguliers ou irréguliers, convexes ou concaves, et malgré tout rester équivalents.

Remarque: Cette relation est parfois appelée équi-extension, un terme utilisé dans les décompositions géométriques.

Un résultat intéressant est que deux polygones équivalents sont aussi équidécomposables. Cela signifie que, par un nombre limité de découpes, on peut réassembler les pièces du premier polygone pour obtenir le second.

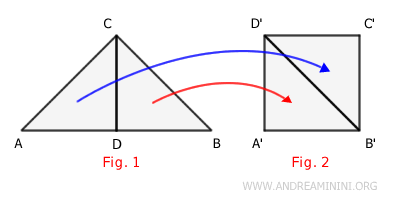
Ce principe est très utile en pratique, notamment pour le calcul de l'aire de polygones irréguliers. En décomposant une figure complexe en formes plus simples, l'évaluation de l'aire devient beaucoup plus accessible.

Cette idée est formalisée par le théorème de Bolyai-Gerwien, qui démontre que tout polygone peut être transformé en un autre polygone équivalent au moyen d'un nombre fini de découpes et de réassemblages.

Reconnaître des polygones équivalents

Il existe plusieurs façons de déterminer si deux polygones ont la même aire, sans effectuer le calcul complet. Ces critères sont issus de la géométrie classique et offrent des outils simples mais puissants.

• Parallélogrammes équivalents
  Deux parallélogrammes ayant la même base et la même hauteur possèdent la même aire.
  
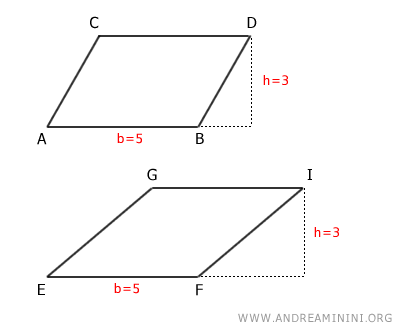
• Triangles équivalents
  Deux triangles ayant la même base et la même hauteur sont équivalents en aire.
  
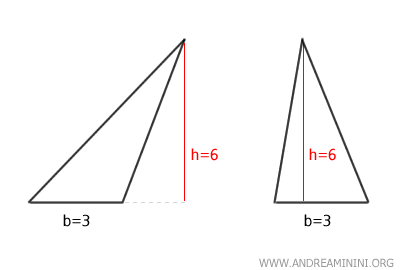
• Triangle et parallélogramme
  Un triangle est équivalent à un parallélogramme ayant la même hauteur et une base égale à la moitié de celle du triangle.
  
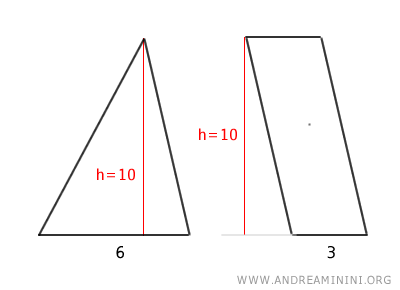
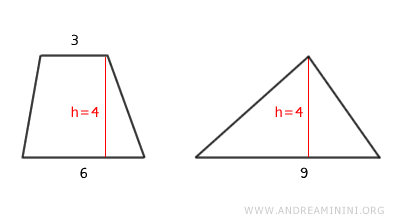
• Triangle et trapèze
  Un trapèze est équivalent à un triangle de même hauteur dont la base est égale à la somme des deux bases du trapèze.
  
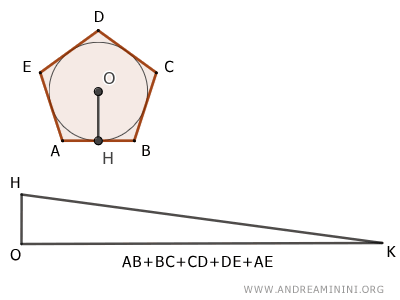
• Triangle et polygone circonscrit
  Un polygone circonscrit à un cercle est équivalent à un triangle dont la hauteur correspond au rayon du cercle et dont la base est le périmètre du polygone.
  

  Cas des polygones réguliers: Tout polygone régulier peut être circonscrit à un cercle, ce qui permet de le ramener à un triangle équivalent très simple à analyser.

Ces critères constituent une base solide pour comparer rapidement des figures et comprendre pourquoi des formes très différentes peuvent néanmoins partager la même aire.

Équivalence et décomposition

En règle générale, deux polygones équivalents sont équidécomposables, mais l'inverse n'est pas automatiquement vrai.

La notion d'équivalence dépasse d'ailleurs le seul cadre des figures planes. Lorsqu'on étudie des solides, on parle d'équivalence en termes de volume.

• L'aire caractérise les figures planes comme les polygones.
• Le volume caractérise les solides comme les polyèdres.

Il est important de distinguer ces deux niveaux, car avoir la même mesure ne garantit pas toujours la possibilité de décomposer et reconstituer les figures.

Exemple: Deux polygones de même aire peuvent toujours être transformés l'un en l'autre par découpe. En revanche, deux polyèdres de même volume ne sont pas forcément équidécomposables, comme l'ont montré des résultats célèbres de la géométrie des solides.

À retenir

Voici quelques résultats complémentaires qui éclairent encore mieux le sujet.

• Théorème de Bolyai-Gerwien
  Tout polygone peut être transformé en un autre polygone équivalent par un nombre fini de découpes.
• Réduction du nombre de côtés
  Un polygone convexe peut être converti en un polygone équivalent ayant un côté de moins.
• Triangle équivalent
  En répétant ce processus, tout polygone convexe à plus de trois côtés peut être ramené à un triangle équivalent.

Ces idées forment un ensemble cohérent de résultats qui montrent comment la géométrie relie, par le biais de l'aire et de la décomposition, des figures parfois très différentes en apparence.