Expérience de Stern-Gerlach
L’expérience de Stern-Gerlach a joué un rôle décisif dans la naissance de la mécanique quantique. Pour la première fois, elle montrait que le spin ne varie pas de manière continue et qu’il ne peut prendre que des valeurs discrètes. Un résultat qui obligeait la physique à abandonner définitivement l’intuition classique du moment angulaire.
En 1922, Otto Stern et Walther Gerlach décidèrent de mettre à l’épreuve une question essentielle. Le moment angulaire d’une particule peut-il pointer dans n’importe quelle direction ou seulement dans quelques orientations bien précises? Le modèle de Bohr-Sommerfeld laissait entrevoir une réponse, mais aucune démonstration directe n’existait encore.
Comment l’expérience a fonctionné
Les deux physiciens envoyèrent un faisceau d’atomes neutres d’argent à travers un champ magnétique très inhomogène. À la sortie, une plaque recouverte de suie enregistrait la position exacte des atomes déviés. Selon la physique classique, on aurait dû observer une trace continue, car les moments magnétiques des atomes devraient se répartir dans toutes les directions.
C’était l’attente naturelle, celle que Stern et Gerlach eux-mêmes partageaient.

Le résultat fut totalement inattendu. Le détecteur ne montra pas une bande uniforme, mais deux taches parfaitement séparées. Aucune valeur intermédiaire n’apparaissait. Les atomes semblaient choisir entre deux orientations possibles et rien d’autre.
Voici le motif réellement observé.
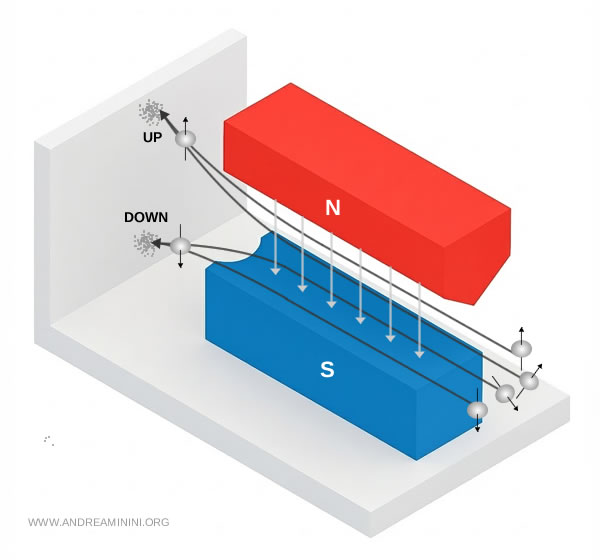
En termes quantiques, la mesure forçait chaque atome à adopter l’un des deux états propres du spin selon l’axe du champ magnétique. La superposition des états disparaissait à l’instant même de la détection. Une particule en apparence libre de toutes les orientations possibles se retrouvait soudain contrainte à n’en choisir qu’une seule.
Nota. Le phénomène rappelle la dualité onde-particule. Un système quantique peut exister dans plusieurs états simultanément, mais toute mesure sélectionne un unique état propre.
Ce que révélait vraiment l’expérience
Le moment angulaire orbital ne suffisait pas pour expliquer ces deux taches nettes. Il manquait une composante essentielle dans la description de l’électron. La réponse vint lorsque Goudsmit et Uhlenbeck avancèrent l’idée d’un moment angulaire intrinsèque qui ne correspond à aucune rotation réelle dans l’espace. Une propriété uniquement quantique: le spin.
Le spin est un nombre quantique fondamental. Il ne se visualise pas, ne correspond à aucun mouvement mécanique et échappe aux représentations géométriques classiques. C’est une propriété de la particule, au même titre que sa charge ou sa masse.
On peut résumer ainsi: le spin n’est pas un mouvement, mais une caractéristique intrinsèque de la particule.
Nota. L’exemple des particules de spin 1/2 est particulièrement éclairant. Après une rotation de 360°, elles ne reviennent pas à leur état initial mais à son opposé.
Il faut une rotation complète de 720° pour retrouver l’état de départ, un comportement sans équivalent en physique classique.
Dans le cas de l’électron, la valeur du spin est $ \frac{1}{2} $. Sa projection sur un axe peut seulement prendre deux valeurs propres.
- spin vers le haut
- spin vers le bas
L’expérience de Stern-Gerlach offrait donc une confirmation directe de la quantification du spin. Une idée théorique devenait un fait expérimental.
Son impact fut immense. Elle contribua à façonner la mécanique quantique moderne et à établir la classification des particules selon leur spin.
- spin 1/2 pour les électrons et les quarks
- spin 1 pour les bosons de jauge
- spin 0 pour le boson de Higgs
- spin 2 pour le graviton hypothétique
L’expérience montrait clairement que le spin est quantifié et non continu. Cette quantification est la clé de distinctions fondamentales, comme la différence entre fermions et bosons ou l’origine du principe d’exclusion de Pauli.
Les fermions ont un spin demi-entier (1/2, 3/2), tandis que les bosons possèdent un spin entier (0, 1, 2).
Au final, un dispositif apparemment simple a révélé une vérité profonde. Le monde quantique n’est pas continu, il est discret. Ce constat fut l’un des piliers de la construction de la mécanique quantique contemporaine.