Fonction quadratique
Une fonction quadratique est une fonction qui peut s’écrire sous la forme $$ y = ax^2 + bx + c $$ avec un coefficient directeur \( a \neq 0 \).
La représentation graphique d’une fonction quadratique est une parabole.
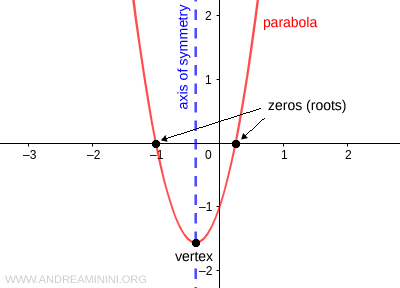
L’axe de symétrie de la parabole est donné par la droite verticale :
$$ x = - \frac{b}{2a} $$
Le sommet de la parabole est le point V :
$$ V \begin{pmatrix} \ - \frac{b}{2a} \ ; \ - \frac{b^2-4ac}{4a} \ \end{pmatrix} $$
Les racines (ou zéros) d’une fonction quadratique sont les valeurs de \( x \) pour lesquelles la parabole coupe l’axe des abscisses. On les appelle “zéros” car en ces points la fonction s’annule, c’est-à-dire \( y=0 \).
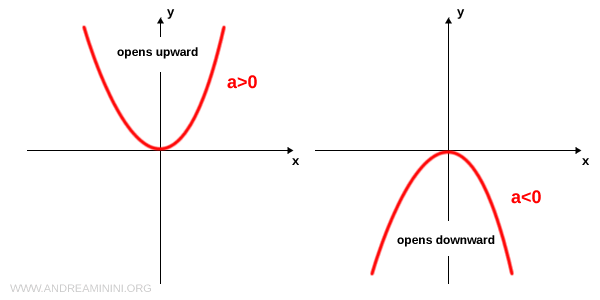
La concavité de la parabole dépend uniquement du signe du coefficient \( a \) :
- a>0
Si \( a>0 \), la parabole est ouverte vers le haut. - a<0
Si \( a<0 \), la parabole est ouverte vers le bas.
La largeur de la parabole dépend de la valeur absolue de \( a \).
Plus le module |a| est grand, plus la parabole est resserrée ; plus il est petit, plus la parabole s’élargit.
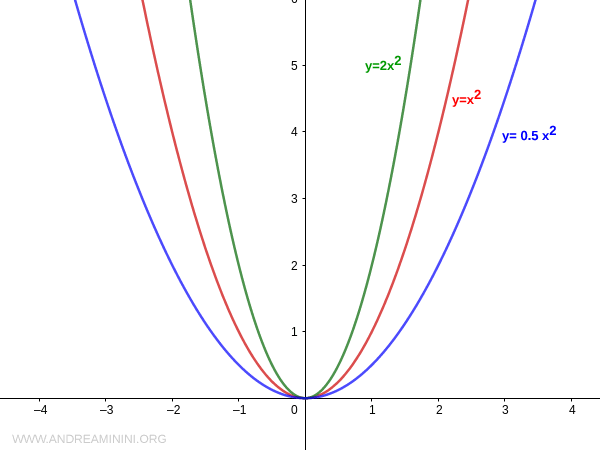
Remarque. L’“ouverture” de la parabole désigne l’écart entre sa courbe et l’axe de symétrie. Une valeur absolue de |a| plus faible élargit la parabole, qui paraît alors s’éloigner de l’axe.
Exemple détaillé
Considérons la fonction quadratique suivante :
$$ y = 4x^2 + 3x - 1 $$
Comme le coefficient directeur est \( a = 4 \), positif, la parabole est ouverte vers le haut.
Pour déterminer les racines (les points d’intersection avec l’axe des abscisses), on résout l’équation quadratique correspondante :
$$ 4x^2 + 3x - 1 = 0 $$
Son discriminant est positif :
$$ \Delta = b^2 - 4ac = 3^2 - 4(4)(-1) = 9 + 16 = 25 $$
L’équation admet donc deux solutions réelles distinctes :
$$ x = \frac{-b \pm \sqrt{\Delta} }{2a} = \frac{-3 \pm \sqrt{25}}{2(4)} = \frac{-3 \pm 5}{8} = \begin{cases} x_1 = \frac{-3 - 5}{8} = -1 \\ \\ x_2 = \frac{-3 + 5}{8} = \tfrac{1}{4} \end{cases} $$
Ainsi, les racines de la fonction quadratique sont \( x_1 = -1 \) et \( x_2 = \tfrac{1}{4} \).
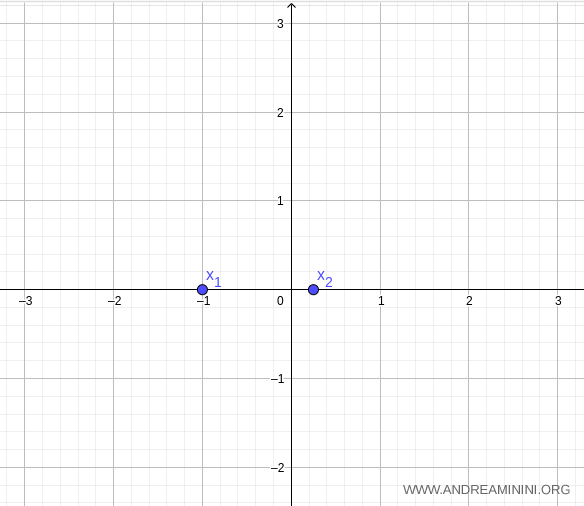
Déterminons maintenant l’axe de symétrie avec \( a=4, b=3, c=-1 \) :
$$ x = - \frac{b}{2a} = - \frac{3}{2 \cdot 4} = - \frac{3}{8} $$
L’axe de symétrie est donc la droite verticale en \( x = -\tfrac{3}{8} \), perpendiculaire à l’axe des abscisses.
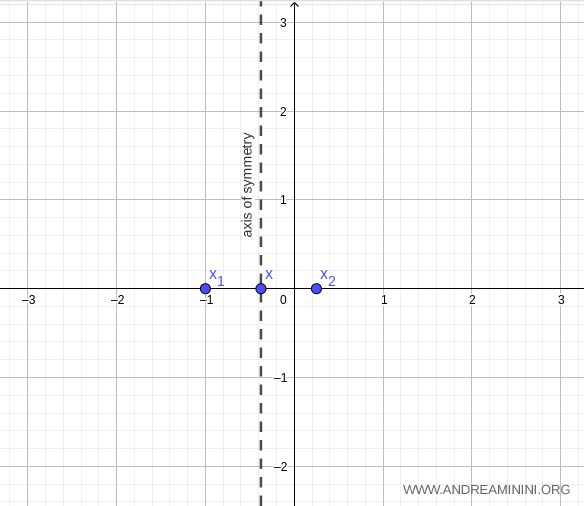
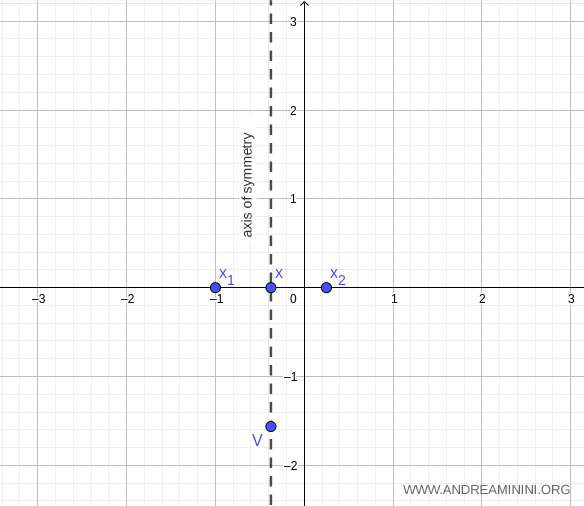
Calculons à présent le sommet de la parabole :
$$ V \begin{pmatrix} \ - \frac{b}{2a} \ ; \ - \frac{b^2-4ac}{4a} \ \end{pmatrix} = \begin{pmatrix} - \tfrac{3}{8} ; - \tfrac{25}{16} \end{pmatrix} $$
Le sommet est donc le point \( V \left(-\tfrac{3}{8}, -\tfrac{25}{16}\right) \).
Pour tracer la courbe avec davantage de précision, on peut calculer des valeurs de \( y \) au voisinage de l’axe de symétrie :
Pour la fonction y = 4x2 + 3x - 1 :
$$ \begin{array}{c|lcr} x & y \\ \hline -2 & 9 \\ -1 & 0 \\ 0 & -1 \\ 1 & 6 \end{array} $$
Ces valeurs permettent de représenter avec justesse le graphique de la parabole :
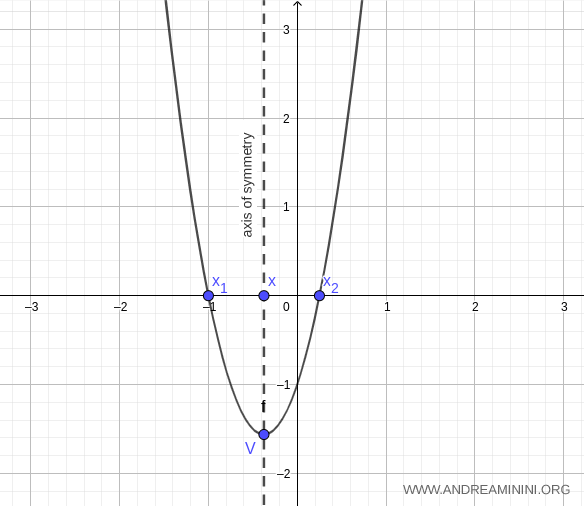
On peut prolonger le tracé en suivant le même procédé.