Points isolés d’un ensemble
Soit \( x_0 \) un nombre réel appartenant à un sous-ensemble \( A \subset \mathbb{R} \). On dit que le point \( x_0 \) est un point isolé de l’ensemble \( A \) s’il existe au moins un voisinage de \( x_0 \) qui ne contient aucun élément de \( A \) autre que \( x_0 \).
D’un point de vue intuitif, cela signifie qu’il est possible de choisir autour de \( x_0 \) un intervalle suffisamment petit pour que son intersection avec l’ensemble \( A \) se réduise au seul point \( x_0 \).
Un voisinage de \( x_0 \) est un intervalle ouvert de la forme
\[ I = (x_0 - r,\; x_0 + r) \]
où \( r > 0 \) est un nombre réel strictement positif.
Le point \( x_0 \) est dit isolé s’il existe au moins une valeur de \( r \) telle que
\[ I \cap A = \{x_0\} \]
Il n’est pas requis que cette condition soit vérifiée pour tous les voisinages de \( x_0 \). L’existence d’un seul voisinage satisfaisant cette propriété suffit.
Comment déterminer si un point est isolé
Pour déterminer si un point \( x_0 \) est isolé :
- on considère un point appartenant à l’ensemble \( A \) ;
- on cherche au moins un voisinage de \( x_0 \) ne contenant aucun autre point de \( A \) ;
- si un tel voisinage existe, le point est isolé. En revanche, si tout voisinage contient d’autres points de l’ensemble, alors le point n’est pas isolé.
Un exemple concret
Considérons l’ensemble \( A \), défini comme une suite de nombres rationnels
\[ A = \left\{ 0, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \dots , \frac{n}{n+1} \right\} \]
où \( n \) désigne un nombre naturel arbitraire.
Représentons cet ensemble sur la droite réelle et portons notre attention sur le point \( 0 \).
On peut alors exhiber un voisinage de \( 0 \) qui ne contient aucun autre élément de \( A \), par exemple \( \left(-\frac{1}{3}, \frac{1}{3}\right) \).
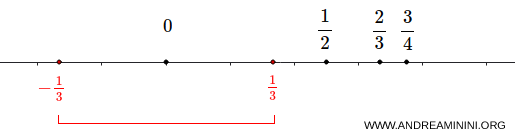
On en déduit que \( 0 \) est un point isolé de l’ensemble \( A \).
Par un raisonnement analogue, et en choisissant des voisinages suffisamment petits, on montre que tous les éléments de l’ensemble \( A \) sont des points isolés.
Remarques
Quelques observations et précisions supplémentaires concernant les points isolés
- Ensembles finis
Si un ensemble contient un nombre fini de points, alors chacun d’eux est un point isolé. Par exemple \[ B = \{-1,\; 0,\; \tfrac{3}{5},\; 6\} \] Cet ensemble est constitué de quatre points distincts. Pour chacun d’eux, on peut construire un voisinage suffisamment petit pour exclure tous les autres. - Ensembles infinis composés uniquement de points isolés
Un ensemble peut être infini tout en étant constitué exclusivement de points isolés. Par exemple, l’ensemble des nombres naturels est infini et chacun de ses éléments est un point isolé \[ \mathbb{N} = \{0,1,2,3,\dots\} \] Pour tout nombre naturel \( n \), il suffit de considérer un voisinage de rayon \( \tfrac{1}{2} \), qui ne contient aucun autre nombre naturel \[ (n-\tfrac{1}{2},\; n+\tfrac{1}{2}) \] On en conclut que tous les nombres naturels sont des points isolés. - Un point isolé n’est jamais un point d’accumulation
Par définition, il existe toujours un voisinage d’un point isolé dans lequel l’ensemble ne contient aucun autre élément. Cette distinction est essentielle dans l’étude des limites de fonctions et dans l’analyse de la structure locale des sous-ensembles de la droite réelle.
Et ainsi de suite.