Serie de Maclaurin de la Función Coseno
La expansión en serie de Maclaurin del coseno es: $$ \cos(x) = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \dots + \frac{(-1)^n x^{2n}}{(2n)!} + o(x^{2n}) $$
Demostración
Partimos de la fórmula general de Maclaurin:
$$ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(0)}{k!}\, x^k + o(x^n) $$
En este caso, f(x) = cos(x).
Para k = 0
Como f(0)(x) = cos(x):
$$ \frac{f^{(0)}(0)}{0!} \cdot x^0 = \frac{\cos(0)}{0!} \cdot 1 = 1 $$
El primer término es:
$$ \cos(x) = 1 + o(1) $$
Para k = 1
La primera derivada es -sen(x):
$$ \frac{f^{(1)}(0)}{1!} \cdot x = \frac{-\sin(0)}{1!} \cdot x = 0 $$
Por tanto:
$$ \cos(x) = 1 + o(x) $$
Para k = 2
La segunda derivada es -cos(x):
$$ \frac{f^{(2)}(0)}{2!} \cdot x^2 = \frac{-\cos(0)}{2!} \cdot x^2 = -\frac{x^2}{2} $$
De modo que:
$$ \cos(x) = 1 - \frac{x^2}{2} + o(x^2) $$
Para k = 3
La tercera derivada es sen(x):
$$ \frac{f^{(3)}(0)}{3!} \cdot x^3 = \frac{\sin(0)}{3!} \cdot x^3 = 0 $$
Así:
$$ \cos(x) = 1 - \frac{x^2}{2} + o(x^3) $$
Para k = 4
La cuarta derivada vuelve a ser cos(x):
$$ \frac{f^{(4)}(0)}{4!} \cdot x^4 = \frac{\cos(0)}{4!} \cdot x^4 = \frac{x^4}{4!} $$
Por tanto, hasta cuarto orden:
$$ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{4!} + o(x^4) $$
Para k = 5
La quinta derivada es -sen(x):
$$ \frac{f^{(5)}(0)}{5!} \cdot x^5 = \frac{-\sin(0)}{5!} \cdot x^5 = 0 $$
De modo que:
$$ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{4!} + o(x^5) $$
En consecuencia, hasta quinto orden:
$$ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{4!} + o(x^5) $$
Gráficamente, la aproximación se muestra así:
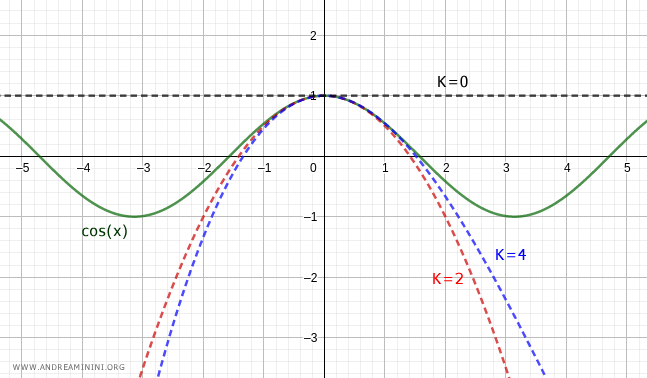
Nota. Los términos de la expansión se alternan entre nulos y no nulos. Por ello, la serie hasta orden 4: $$ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{4!} + o(x^4) $$ y hasta orden 5: $$ \cos(x) = 1 - \frac{x^2}{2} + \frac{x^4}{4!} + o(x^5) $$ son esencialmente idénticas, diferenciándose solo en el orden del término de resto.
Y así sucesivamente.