El Número Áureo
El Número Áureo es aproximadamente el número irracional: $$\phi = 1.6180339887...$$
Suele representarse con la letra griega φ (phi).
Este número irracional ha fascinado durante siglos a matemáticos, artistas y arquitectos por sus propiedades únicas y su supuesta relación con la estética y la armonía en la naturaleza.
Nota. Desde la Antigüedad, se ha considerado que las proporciones basadas en el Número Áureo resultan especialmente agradables a la vista. Esto ha motivado su uso en múltiples campos, desde la pintura y la escultura hasta la arquitectura. Por ejemplo, el Partenón de Atenas incorpora proporciones relacionadas con el Número Áureo, al igual que muchas obras del Renacimiento. También se afirma que aparece en fenómenos naturales, como en la espiral de la concha del nautilus, aunque algunas de estas supuestas apariciones en la naturaleza están probablemente exageradas.
¿Cómo se obtiene?
El Número Áureo se define considerando dos segmentos, \(a\) y \(b\), con \(a > b\), de modo que la razón entre la longitud total (\(a + b\)) y el segmento mayor (\(a\)) sea igual a la razón entre el segmento mayor (\(a\)) y el menor (\(b\)). Matemáticamente se expresa así:
$$ \frac{a + b}{a} = \frac{a}{b} = \phi $$
Esta relación conduce al valor:
$$ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887... $$
Demostración
Veamos por qué la razón entre el segmento mayor “a” y el menor “b” resulta ser aproximadamente 1.618...
Partimos de la relación fundamental entre ambos segmentos:
$$ \frac{a + b}{a} = \frac{a}{b} = \phi $$
La razón entre la suma de los segmentos (\(a + b\)) y el segmento mayor \(a\) es igual a \(\phi\):
$$ \frac{a + b}{a} = \phi $$
Asimismo, la razón entre el segmento mayor \(a\) y el menor \(b\) también es \(\phi\):
$$ \phi = \frac{a}{b} $$
De esta ecuación se deduce que el segmento \(b\) es igual a \( \frac{a}{\phi} \):
$$ b = \frac{a}{\phi} $$
Sustituyendo esta expresión en la primera ecuación:
$$ \frac{a + \frac{a}{\phi}}{a} = \phi $$
Simplificando:
$$ 1 + \frac{1}{\phi} = \phi $$
De donde se obtiene:
$$ \frac{1}{\phi} = \phi - 1 $$
Multiplicando ambos miembros por \(\phi\), se obtiene una ecuación cuadrática:
$$ 1 = \phi^2 - \phi $$
Reordenando términos:
$$ \phi^2 - \phi - 1 = 0 $$
Que se resuelve mediante la fórmula general:
$$ \phi = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Con \(a = 1\), \(b = -1\) y \(c = -1\). Sustituyendo estos valores, se obtiene:
$$ \phi = \frac{-(-1) \pm \sqrt{(-1)^2 - 4 \cdot 1 \cdot (-1)}}{2 \cdot 1} = \frac{1 \pm \sqrt{5}}{2} $$
Como \(\phi\) es positivo, se toma la solución positiva:
$$ \phi = \frac{1 + \sqrt{5}}{2} \approx 1.6180339887... $$
Así se demuestra cómo esta relación conduce directamente al valor del Número Áureo, mediante sencillos pasos algebraicos y el uso de la fórmula cuadrática.
Ejemplo práctico
El Número Áureo está íntimamente relacionado con la sucesión de Fibonacci, en la cual cada número es la suma de los dos anteriores (0, 1, 1, 2, 3, 5, 8, 13, 21, ...).
$$ \sigma = 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... $$
La razón entre términos consecutivos en la sucesión de Fibonacci tiende al valor del Número Áureo conforme se avanza en la serie:
$$ \frac{1}{1}, \ \frac{2}{1}, \ \frac{3}{2}, \ \frac{5}{3}, \ \frac{8}{5}, \ \frac{13}{8}, \ \frac{21}{13}, \ \frac{34}{21}, \ ... $$
Calculando estos cocientes se observa cómo se aproximan cada vez más a 1.618...
$$ 1, \ 2, \ 1.5, \ 1.666..., \ 1.6, \ 1.625, \ 1.615, \ 1.619, \ ... $$
Observaciones
Algunas observaciones adicionales sobre el Número Áureo:
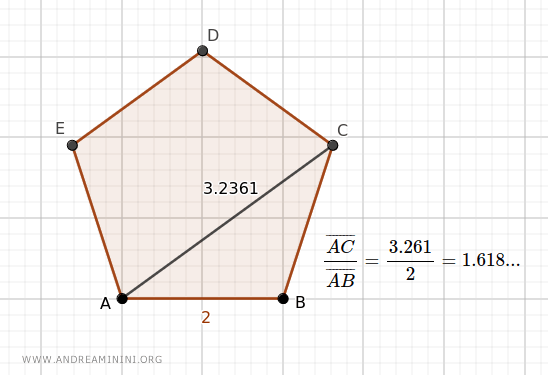
- La razón entre la diagonal y el lado de un pentágono regular equivale al Número Áureo
Por ejemplo, la razón entre la diagonal AC de un pentágono regular y su lado AB es aproximadamente 1.618...
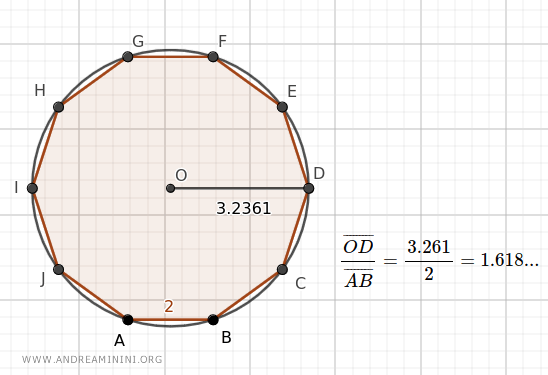
- La razón entre el radio de una circunferencia y el lado de un decágono regular inscrito equivale al Número Áureo
En este decágono regular, la razón entre el radio de la circunferencia (3.2361) y el lado del decágono (2) es igual al Número Áureo.