El Lado de un Decágono Regular es la Sección Áurea de su Radio
El lado de un decágono regular corresponde a la sección áurea del radio de su circunferencia circunscrita: $$ r : l = l : (r - l) $$ 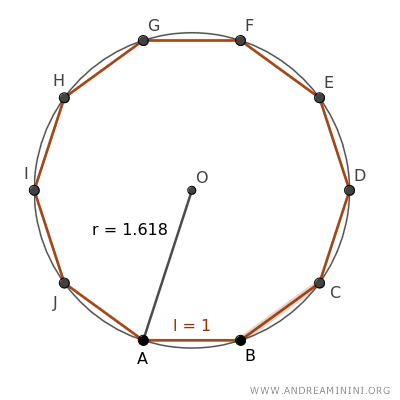
En otras palabras, en un decágono regular, la razón entre el radio de la circunferencia circunscrita y el lado del decágono es igual al número áureo, aproximadamente 1.618...
Ejemplo Práctico
Consideremos un decágono regular cuyo lado mide 1 unidad.
El radio de la circunferencia circunscrita a este decágono es igual a 1.618..., es decir, coincide con el número áureo.

El segmento AK es congruente al lado AB y, por lo tanto, mide también 1 unidad.
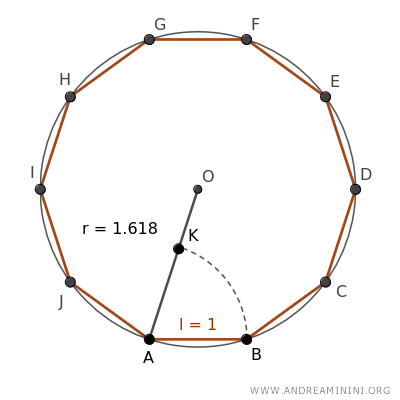
Verifiquemos ahora si se cumple la proporción áurea:
$$ \overline{AB} : \overline{AK} = \overline{AK} : \overline{OK} $$
Sabiendo que OK = 1 y AB = 1.618...
$$ 1.618 : 1 = 1 : \overline{OK} $$
El segmento OK es igual a la diferencia entre OA y AK, es decir, 1.618 - 1 = 0.618.
$$ 1.618 : 1 = 1 : 0.618 $$
Al efectuar ambas divisiones, se obtiene el mismo resultado:
$$ 1.618 = 1.618 $$
Por tanto, se cumple la proporción, y el lado (AB) del decágono constituye la sección áurea del radio (OA) de la circunferencia circunscrita.
Demostración
Construyamos un decágono regular, es decir, un polígono de 10 lados iguales.
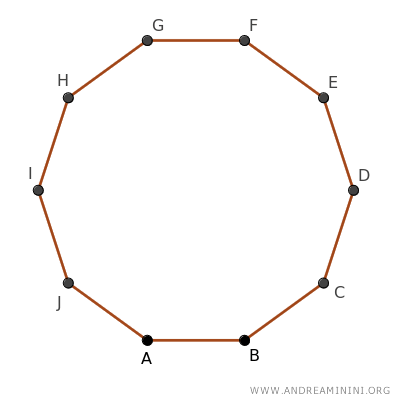
Todos los polígonos regulares pueden inscribirse en una circunferencia.
Por tanto, determinamos el centro del decágono para trazar la circunferencia circunscrita, con centro en O y radio r.
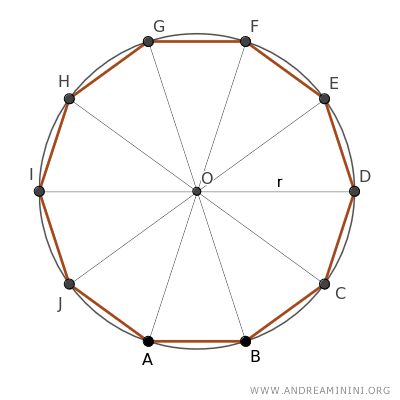
Esto divide el decágono en 10 triángulos congruentes, pues, según el tercer criterio de congruencia de triángulos, todos tienen lados iguales.
$$ ABO \cong BCO \cong CDO \cong ... $$
Cada uno de estos triángulos tiene un ángulo en el vértice O de 36°, ya que el ángulo completo (360°) se reparte en 10 partes iguales.
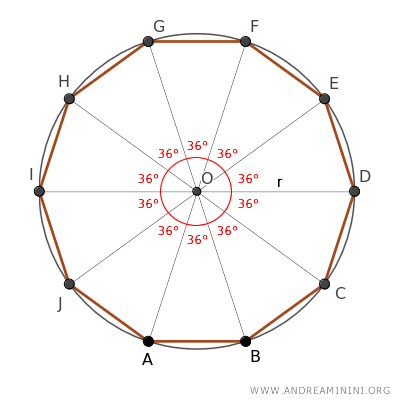
Nos centraremos en el triángulo ABO, pues lo que se demuestre en uno de ellos es válido para todos debido a su congruencia.
El triángulo ABO es un triángulo isósceles porque tiene dos lados congruentes AO ≅ BO, que corresponden al radio de la circunferencia.
Al ser isósceles, presenta dos ángulos en la base α ≅ β congruentes.
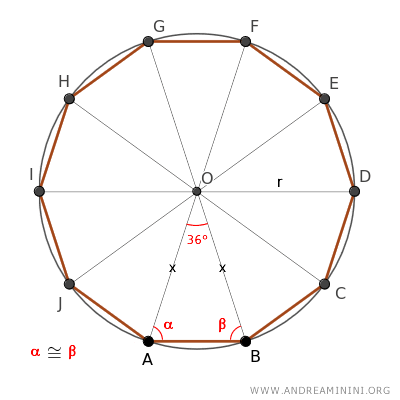
La suma de los ángulos interiores de cualquier triángulo siempre es 180°:
$$ \alpha + \beta + 36° = 180° $$
Por tanto, la suma de α + β es:
$$ \alpha + \beta = 180° - 36° $$
$$ \alpha + \beta = 144° $$
Como sabemos que α ≅ β, cada uno mide la mitad de 144°, es decir, α = 72° y β = 72°.
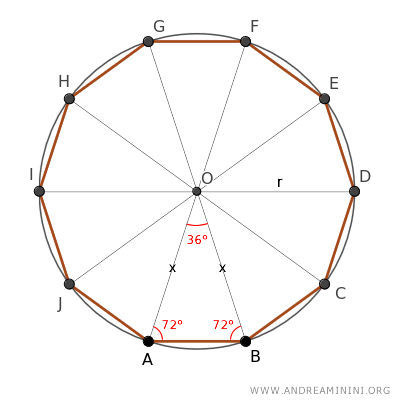
A continuación, trazamos la bisectriz de uno de los ángulos adyacentes a la base del triángulo ABO, dividiendo el ángulo de 72° en dos ángulos de 36°.
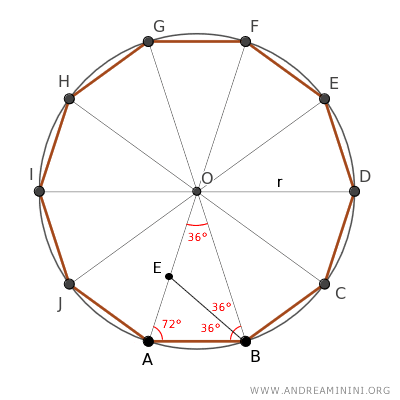
El triángulo BOE resulta también isósceles, pues tiene dos ángulos de 36° junto a la base OB.
Por tanto, sus lados oblicuos OE ≅ BO son congruentes.
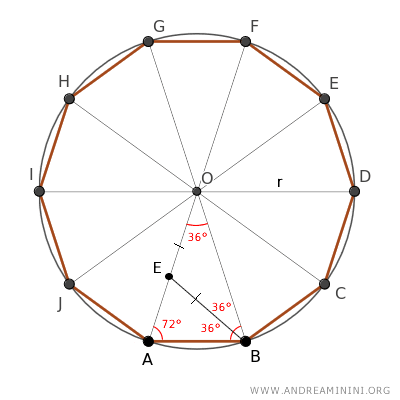
Al examinar el triángulo ABE, observamos que ya conocemos dos de sus ángulos, por lo que deducimos el tercero por diferencia: 180° - 72° - 36° = 72°.
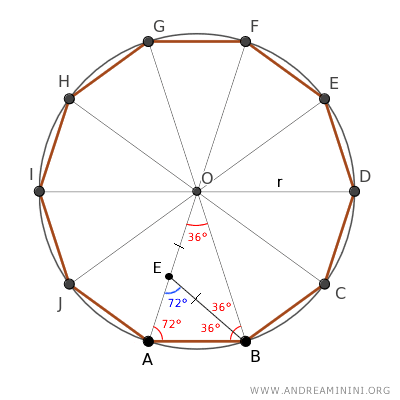
Por tanto, el triángulo ABE es también isósceles, pues posee dos ángulos congruentes de 72°.
En consecuencia, sus lados oblicuos AB ≅ BE son iguales.
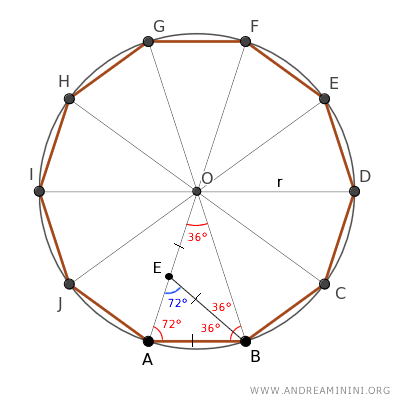
Como AB ≅ EB y EB ≅ OE, se deduce que AB ≅ OE.
Los triángulos ABO y ABE son semejantes porque, según el primer criterio de semejanza de triángulos, poseen dos ángulos congruentes (36° y 72°).
$$ ABO \approx ABE $$
Siendo semejantes, sus lados correspondientes están en proporción:
$$ \overline{OB} : \overline{AB} = \overline{AB} : \overline{EA} $$
Donde OB es el radio (r) de la circunferencia y AB es el lado (l) del decágono.
$$ r : l = l : \overline{EA} $$
El segmento EA es la diferencia entre OA y OE:
$$ \overline{EA} = \overline{OA} - \overline{OE} $$
Como OA es el radio y OE ≅ AB, que coincide con el lado (l) del decágono:
$$ \overline{EA} = r - l $$
Así, el segmento EA es la diferencia entre el radio y el lado del decágono.
$$ r : l = l : (r - l) $$
Esto demuestra que, en un decágono regular, el radio (r) de la circunferencia circunscrita está en la misma proporción con el lado (l) del decágono que el lado (l) con la diferencia (r - l).
Por tanto, el lado (l) es la media proporcional entre el radio (r) y el segmento (r - l), es decir, constituye la sección áurea del radio.
Y así sucesivamente.