Proporción Áurea
La Proporción Áurea de un segmento es aquella división especial que establece una relación única, en la que una parte del segmento actúa como media proporcional entre la longitud total y la longitud de la parte restante.
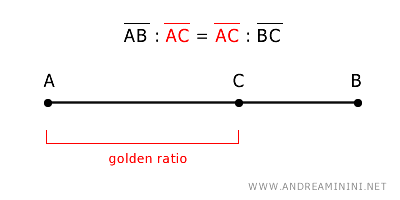
La Proporción Áurea es también conocida como la divina proporción, número áureo o Phi (representada por φ).
Se trata de una relación matemática excepcional que aparece con frecuencia en la naturaleza, el arte, la arquitectura y otros muchos ámbitos.
Nota. Los antiguos griegos consideraban la Proporción Áurea como la máxima expresión de la armonía en las medidas. Las proporciones basadas en este número suelen percibirse como equilibradas y agradables a la vista. Muchos fenómenos naturales se ajustan de forma sorprendente a la Proporción Áurea: las proporciones del cuerpo humano, la disposición de las hojas en las plantas, la forma de ciertos moluscos, etc. Por este motivo, ha sido empleada durante siglos en arte y arquitectura, como en el Partenón de Atenas, el Hombre de Vitruvio de Leonardo da Vinci y muchas otras obras.
Imaginemos, por ejemplo, un segmento AB que se divide en dos partes: AC y CB.
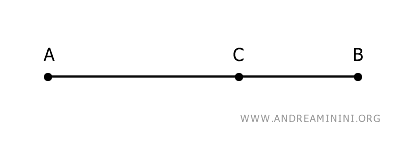
Diremos que el segmento AC está en Proporción Áurea con respecto a AB si se cumple la siguiente proporción:
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{CB} $$
En otras palabras, AC es la media proporcional entre la longitud total del segmento AB y la longitud de la parte restante CB.
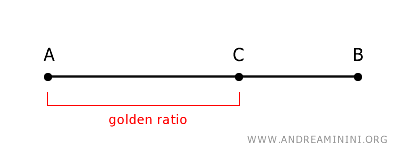
La razón entre la longitud del segmento áureo AC y la longitud total AB es una constante cuyo valor aproximado es 0,618033988749895.
$$ \frac{ \overline{AC} }{ \overline{AB} } = 0,618033988749895 $$
Por otro lado, la razón entre la longitud del segmento completo AB y la del segmento áureo AC es 1,618033988749895, conocido como el número áureo (φ).
$$ \frac{ \overline{AB} }{ \overline{AC} } = 1,618033988749895 = \phi $$
Así, para determinar la longitud del segmento áureo en un segmento dado, basta multiplicar la longitud total AB por el factor aproximado de 0,618:
$$ \overline{AC} = 0,618 \cdot \overline{AB} $$
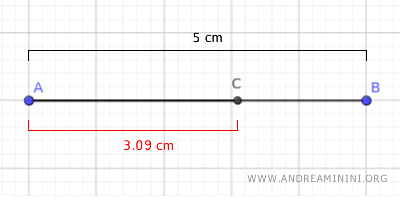
Por ejemplo, si el segmento AB mide 5 cm,
la longitud del segmento áureo AC será 0,618 · 5 cm = 3,09 cm.
$$ \overline{AC} = 0,618 \cdot 5 \text{ cm} = 3,09 \text{ cm} $$
¿Cómo se obtiene el valor 0,618? Para deducirlo de forma algebraica, consideramos un segmento AB de longitud unidad (AB = 1) y llamamos x a la longitud del segmento áureo. $$ 1 : x = x : (1 - x) $$ Aplicamos la propiedad fundamental de las proporciones: $$ x \cdot x = 1 \cdot (1 - x) $$ $$ x^2 = 1 - x $$ $$ x^2 + x - 1 = 0 $$ Resolviendo la ecuación cuadrática: $$ x = \frac{-1 \pm \sqrt{1^2 - 4 \cdot 1 \cdot (-1)}}{2} $$ $$ x = \frac{-1 \pm \sqrt{5}}{2} = \begin{cases} \frac{-1 - \sqrt{5}}{2} = \text{no válido} \\ \\ \frac{-1 + \sqrt{5}}{2} = 0,618033 \end{cases} $$
Cómo construir la Proporción Áurea en un segmento
Consideremos un segmento AB.

Localiza su punto medio M y traza desde el extremo B una perpendicular hacia afuera.
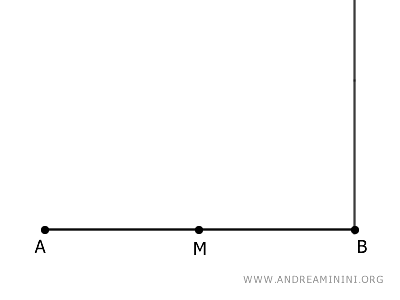
Con el compás centrado en el punto B y abertura igual a BM, traza un arco que corte a la perpendicular en el punto C.
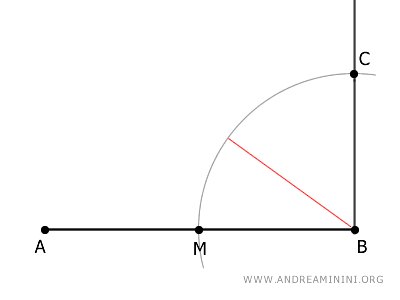
Une los puntos A y C con un segmento.
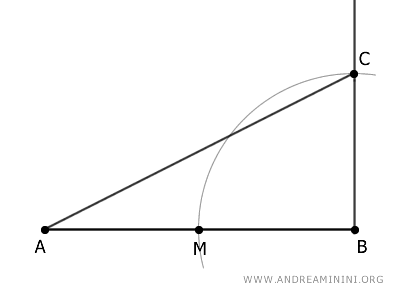
A continuación, con el compás centrado en C y abertura igual a CB, traza un arco que corte al segmento AC en el punto D.
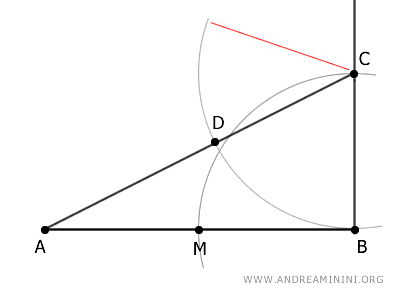
Después, coloca el compás en el punto A, con abertura igual a AD, y dibuja un arco que corte al segmento AB en el punto E.
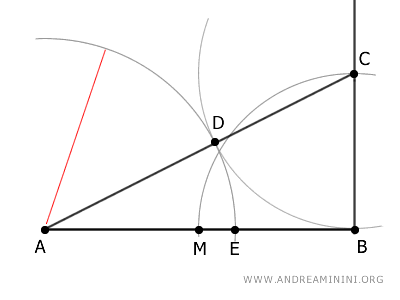
El segmento AE es la sección áurea del segmento AB.
Demostración
Para demostrar la proporción áurea, consideremos el procedimiento de construcción empleado para obtener el segmento áureo AE.
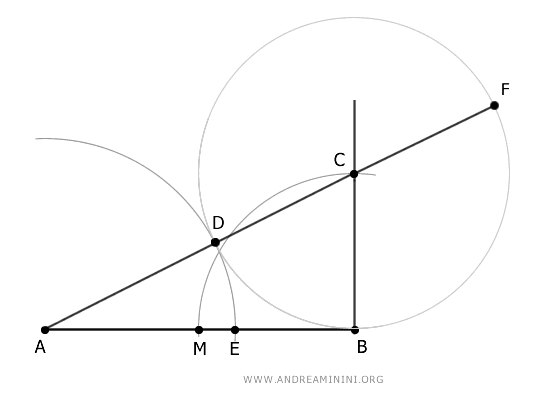
El segmento AB es la tangente de la circunferencia de centro C, mientras que AF es una secante.
Según el Teorema de la Secante y la Tangente, estos segmentos están en proporción:
$$ \overline{AF} : \overline{AB} = \overline{AB} : \overline{AD} $$
Aplicamos la propiedad de disociación de proporciones:
$$ ( \overline{AF} - \overline{AB} ) : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
Dado que la circunferencia tiene radio OB ≅ BM, su diámetro CE es congruente al segmento AB.
$$ ( \overline{AF} - \overline{CE} ) : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
Observamos que AF - CE equivale al segmento AD.
$$ \overline{AD} : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AD} $$
Asimismo, el segmento AD es congruente al segmento áureo AE.
$$ \overline{AE} : \overline{AB} = ( \overline{AB} - \overline{AD} ) : \overline{AE} $$
Por tanto, AB - AD es congruente a AB - AE.
$$ \overline{AE} : \overline{AB} = ( \overline{AB} - \overline{AE} ) : \overline{AE} $$
La diferencia AB - AE, es decir EB, representa la parte restante del segmento AB tras eliminar la sección áurea AE.
$$ \overline{AE} : \overline{AB} = \overline{EB} : \overline{AE} $$
Finalmente, aplicamos la propiedad de permutación de proporciones:
$$ \overline{AB} : \overline{AE} = \overline{AE} : \overline{EB} $$
Esto demuestra que el segmento AB se relaciona con la sección áurea AE del mismo modo que AE se relaciona con el segmento restante EB.
Por lo tanto, el segmento AE es la sección áurea del segmento AB.
El Rectángulo Áureo
Se denomina Rectángulo Áureo aquel en el que la razón entre el lado mayor y el lado menor es igual a la Proporción Áurea, φ ≈ 1,618…
Por ejemplo, el siguiente rectángulo es un Rectángulo Áureo.
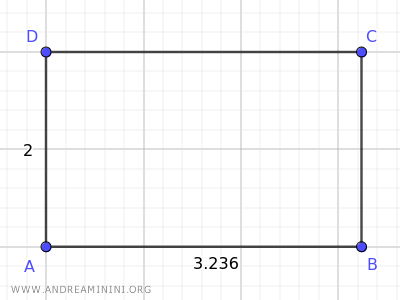
La relación entre la longitud del lado mayor (3,235) y la del lado menor (2) es aproximadamente igual a la Proporción Áurea (1,618).
$$ \frac{ \overline{AB} }{ \overline{AD} } = \frac{3,236}{2} = 1,618 $$
Si se elimina del Rectángulo Áureo el cuadrado formado por el lado menor, el rectángulo restante sigue siendo un Rectángulo Áureo.
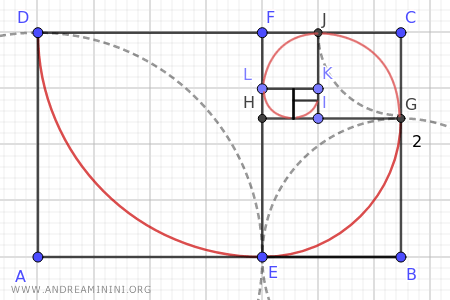
Este encadenamiento de Rectángulos Áureos genera una curva en espiral que se observa en numerosas estructuras naturales, como en las conchas de algunos moluscos, y constituye un motivo frecuente en el arte y la arquitectura.
Y así sucesivamente.