Forme en intercepts de l’équation d’un plan
La forme en intercepts d’un plan s’obtient en déterminant les valeurs $p$, $q$ et $r$, de telle sorte que son équation cartésienne puisse s’écrire :
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
L’équation cartésienne générale d’un plan est :
$$ ax + by + cz + d = 0 $$
En annulant successivement deux variables, on calcule les points d’intersection avec les axes :
Si $y = z = 0$ :
$$ ax + d = 0 \\ ax = -d \\ x = -\frac{d}{a} $$
Si $x = z = 0$ :
$$ by + d = 0 \\ by = -d \\ y = -\frac{d}{b} $$
Si $x = y = 0$ :
$$ cz + d = 0 \\ cz = -d \\ z = -\frac{d}{c} $$
On en déduit les intercepts :
$$ p = -\frac{d}{a}, \quad q = -\frac{d}{b}, \quad r = -\frac{d}{c} $$
On obtient ainsi la forme en intercepts du plan :
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
Intérêt de la forme en intercepts
Les valeurs $p$, $q$ et $r$ correspondent directement aux coordonnées des points où le plan coupe les axes de référence :
- $p$ = intersection avec l’axe $x$
- $q$ = intersection avec l’axe $y$
- $r$ = intersection avec l’axe $z$
Exemple
Considérons le plan défini par l’équation :
$$ -5x - y + 8z + 15 = 0 $$
Pour $y = z = 0$, on obtient l’intersection avec l’axe $x$ :
$$ -5x + 15 = 0 \\ x = \frac{15}{5} = 3 $$
Pour $x = z = 0$, on obtient l’intersection avec l’axe $y$ :
$$ -y + 15 = 0 \\ y = 15 $$
Pour $x = y = 0$, on obtient l’intersection avec l’axe $z$ :
$$ 8z + 15 = 0 \\ 8z = -15 \\ z = -\frac{15}{8} $$
Les intercepts du plan sont donc :
$$ p = 3, \quad q = 15, \quad r = -\frac{15}{8} $$
D’où la forme en intercepts de son équation :
$$ \frac{x}{p} + \frac{y}{q} + \frac{z}{r} = 1 $$
$$ \frac{x}{3} + \frac{y}{15} + \frac{z}{-\tfrac{15}{8}} = 1 $$
Dans cette forme, les dénominateurs indiquent précisément les coordonnées des points où le plan coupe les trois axes de coordonnées.
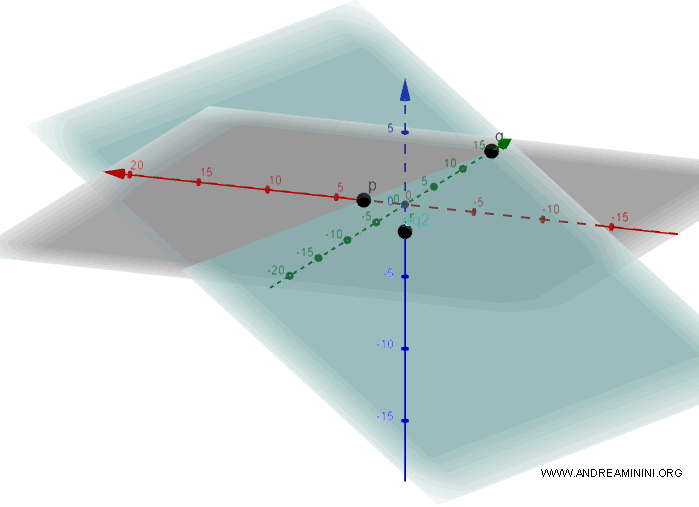
Remarque. La figure ci-dessous illustre le plan et ses points d’intersection $p$, $q$ et $r$.